L'expression du périmètre et de l'aire de polygones au moyen de variables consiste à représenter le périmètre ou l'aire à l'aide d'une expression algébrique.
On utilise la méthode algébrique pour exprimer le périmètre ou l'aire d'une figure lorsqu'il manque des valeurs numériques aux mesures impliquées. Ainsi, à défaut de pouvoir utiliser une valeur numérique, une variable viendra remplacer les valeurs inconnues.
L'utilisation de variables et d'expression algébriques permet de généraliser la mesure recherchée. Dans le cas du périmètre, l'expression algébrique permettra d'évaluer le périmètre en changeant simplement une variable par une valeur précise. Ainsi, on évite de refaire les calculs à chaque fois.
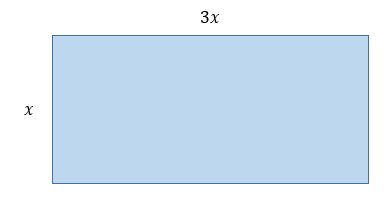
Si la longueur d'un rectangle vaut le triple de sa largeur,
a) quelle est l'expression algébrique associée à son périmètre?
b) quel est son périmètre si la largeur mesure 10 cm?
c) quel est son périmètre si la largeur mesure 4,7 cm?
1. Faire un dessin et poser les variables/expressions algébriques
|\begin{align*}
x &= \text{Largeur du rectangle}\\
3x &= \text{Longeur du rectangle}\end{align*}|
2. Trouver l'expression algébrique associée au périmètre (question a) )
P_\text{rectangle} &= 2\times \text{largeur} + 2\times \text{longueur} \\
&= 2 (x) + 2 (3x) \\
&= 2x + 6x \\
&= 8x
\end{align*}|
3. Évaluer l'expression algébrique selon la valeur donnée
b) Si la largeur vaut 10 cm?
P_\text{rectangle} &= 8x \\
&= 8 (10) \\
&= 80\ \text{cm}
\end{align*}|
c) Si la largeur vaut 4,7 cm?
P_\text{rectangle} &= 8x \\
&= 8 (4,7) \\
&= 37,6\ \text{cm}
\end{align*}|
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Il est possible d'en connaitre davantage sur la représentation algébrique du périmètre des polygones réguliers en consultant la fiche : <a href="/fr/eleves/bv/mathematiques/les-mesures-manquantes-d-une-figure-plane-1-varia-m1211">le périmètre d'un polygone régulier exprimé à l'aide de variables.</a></span></p>
</body></html>
Il est possible d'exprimer une surface d'une figure plane à l'aide d'une expression algébrique. Cette représentation est utilisée lorsque les valeurs numériques sont inconnues. Ainsi, elles sont remplacées par des expressions algébriques.
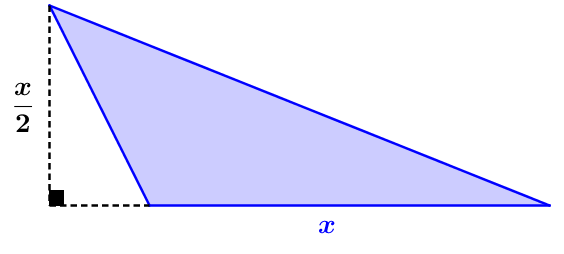
Si la mesure de la hauteur d'un triangle vaut la moitié de celle de sa base,
a) quelle est l'expression algébrique associée à son aire?
b) quelle est son aire si la mesure de la base est 12,5 cm?
1. Faire un dessin et poser les variables/expressions algébriques
|\begin{align*}
x &= \text{mesure de la base du triangle} \\ \\
\frac{x}{2} &= \text{mesure de la hauteur du triangle}
\end{align*}|
2. Trouver l'expression algébrique associée à l'aire (question a) )
A_\text{triangle} &= \frac{\text{base} \times \text{hauteur}}{2} \\ \\
&=\dfrac{x \left(\frac{x}{2}\right)}{2} \\ \\
&= \frac{\frac{x^2}{2}}{2} \\ \\
&= \frac{x^2}{4}
\end{align*}|
3. Évaluer l'expression algébrique selon la valeur donnée
b) Si la base vaut 12,5 cm?
A_\text{triangle} &= \frac{x^2}{4} \\ \\
&= \frac{12,5^2}{4} \\ \\
&\approx 39,06 \ \text{cm}^2
\end{align*}|
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Il est possible d'en connaitre davantage sur l'utilisation d'expression algébrique et l'aire des polygones réguliers en consultant la fiche :<a href="/fr/eleves/bv/mathematiques/les-mesures-manquantes-d-une-figure-decomposable-1-variable-m1212"> l'aire d'un polygone régulier exprimée à l'aide de variable.</a></span></p>
</body></html>