Il peut arriver qu’on demande de trouver une ou plusieurs mesures manquantes à partir du périmètre ou à partir de l’aire d’une figure. Pour résoudre les problèmes en lien avec l’aire, il est utile de connaitre les formules pour calculer l’aire des différentes figures planes. Voici les étapes à suivre pour résoudre ce type de problème.
-
Déterminer la formule pour calculer l’aire à utiliser.
-
Remplacer les variables par les valeurs connues.
-
Isoler l’inconnue.
-
Répondre à la question.
Voici une série d’exemples. Les premiers sont des problèmes de géométrie qui ne proviennent pas d’un contexte particulier, tandis que le dernier est un problème écrit qui présente une courte mise en situation.
Trouve le côté du carré suivant.

-
Déterminer la formule
On utilise la formule pour calculer l’aire d’un carré.||A= c^2|| -
Remplacer les variables par les valeurs connues
||\color{#3a9a38}{121}= c^2|| -
Isoler l’inconnue
||\begin{align}\color{#ec0000}{\sqrt{\color{black}{121}}}&=\color{#ec0000}{\sqrt{\color{black}{c^2}}}\\11&=c \end{align}|| -
Répondre à la question
Le côté du carré est de |11\ \text{cm}.|
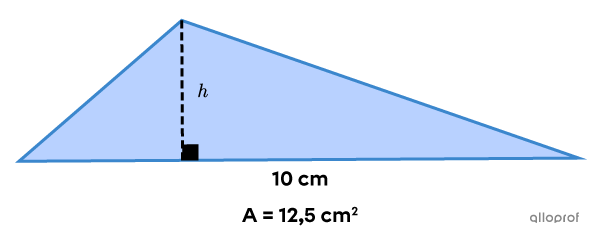
Trouve la hauteur du triangle suivant.
-
Déterminer la formule
On utilise la formule pour calculer l’aire d’un triangle.||A=\dfrac{b\times h}{2}|| -
Remplacer les variables par les valeurs connues
||\color{#3a9a38}{12{,}5} =\dfrac{\color{#3a9a38}{10} \times h}{2}|| -
Isoler l’inconnue
||\begin{align}12{,}5\color{#ec0000}{\times 2}&=\dfrac{10 h}{2} \color{#ec0000}{\times 2}\\25&=10 h\\ \color{#ec0000}{\dfrac{\color{black}{25}}{10}}&=\color{#ec0000}{\dfrac{\color{black}{10 h}}{10}}\\ 2{,}5 &= h\end{align}|| -
Répondre à la question
La hauteur du triangle est de |2{,}5\ \text{cm}.|
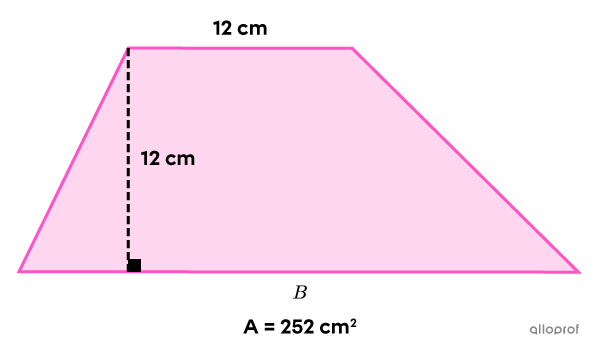
Trouve la grande base dans le trapèze suivant.
-
Déterminer la formule
On utilise la formule pour calculer l’aire d’un trapèze.||A=\dfrac{(B+b)\times h}{2}|| -
Remplacer les variables par les valeurs connues
||\color{#3a9a38}{252}=\dfrac{(B+ \color{#3a9a38}{12})\times \color{#3a9a38}{12}}{2}|| -
Isoler l’inconnue
||\begin{align}252&=\dfrac{12B+ 144}{2}\\252 \color{#ec0000}{\times 2}&= \dfrac{12B+144}{2}\color{#ec0000}{\times 2}\\ 504&= 12B+ 144\\ 504\color{#ec0000}{-144}&= 12B+ 144\color{#ec0000}{-144}\\360&=12B\\ \color{#ec0000}{\dfrac{\color{black}{360}}{12}}&= \color{#ec0000}{\dfrac{\color{black}{12B}}{12}}\\ 30&=B\end{align}|| -
Répondre à la question
Ainsi, la grande base est de |30\ \text{cm}.|
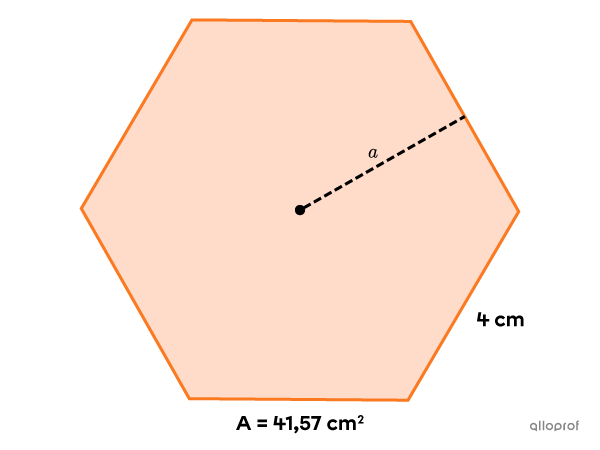
Trouve l’apothème de l’hexagone régulier suivant.
-
Déterminer la formule
On utilise la formule pour calculer l’aire d’un polygone régulier.||A=\dfrac{c\times a\times n}{2}|| -
Remplacer les variables par les valeurs connues
Puisqu’il s’agit d’un hexagone, on a |n=6.|||\color{#3a9a38}{41{,}57}=\dfrac{\color{#3a9a38}4 \times a \times \color{#3a9a38}6}{2}|| -
Isoler l’inconnue
||\begin{align}41{,}57&=\dfrac{24a}{2}\\41{,}57&=12a\\\color{#ec0000}{\dfrac{\color{black}{41{,}57}}{12}}&= \color{#ec0000}{\dfrac{\color{black}{12a}}{12}}\\ 3{,}46 &\approx a \end{align}|| -
Répondre à la question
L'apothème de l'hexagone régulier est d’environ |3{,}46\ \text{cm}.|
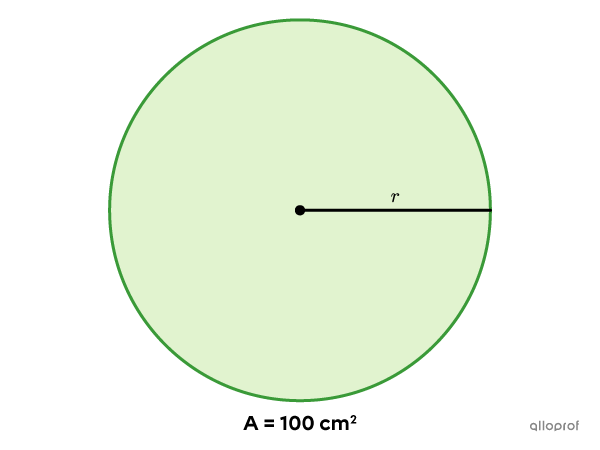
Trouve le rayon du disque suivant.
-
Déterminer la formule
On utilise la formule pour calculer l’aire d’un disque.||A=\pi r^2|| -
Remplacer les variables par les valeurs connues
||\color{#3a9a38}{100}=\pi r^2|| -
Isoler l’inconnue
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{100}}{\pi}} &= \color{#ec0000}{\dfrac{\color{black}{\pi r^2}}{\pi}}\\31{,}83&\approx r^2\\ \color{#ec0000}{\sqrt{\color{black}{31{,}83}}}&\approx \color{#ec0000}{\sqrt{\color{black}{r^2}}} \\ 5{,}64 &\approx r \end{align}|| -
Répondre à la question
Le rayon du disque est d’environ |5{,}64\ \text{cm}.|
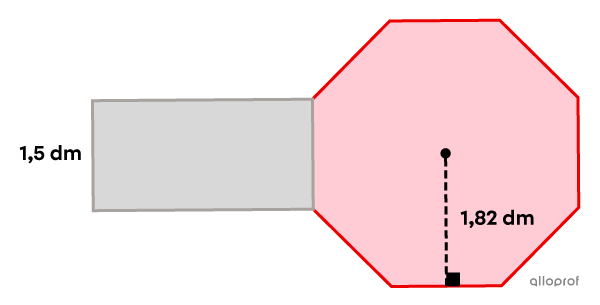
Afin d'assurer une sécurité maximale, une compagnie de transport scolaire tient à recouvrir de lumières scintillantes le contour du bras d'arrêt de ses autobus. Ce bras est formé d'un rectangle et d'un octogone régulier.
Sachant que l'aire totale de cette figure est de |15{,}42\ \text{dm}^2,| détermine combien de lumières on peut installer sur le contour du bras d’arrêt si la compagnie veut en installer à tous les |5\ \text{cm}.|
-
Déterminer la formule
On utilise les formules pour calculer l’aire du rectangle et l’aire de l’octogone régulier.||\begin{align}A_\text{totale}&=A_\text{rectangle}+A_\text{octogone}\\A_\text{totale}&=b \times h + \dfrac{c\times a\times n}{2}\end{align}|| -
Remplacer les variables par les valeurs connues
La mesure du côté de l’octogone est la même que la hauteur du rectangle. De plus, comme il s’agit d’un octogone, on a |n=8.|||\color{#3a9a38}{15{,}42}=b\times \color{#3a9a38}{1{,}5} + \dfrac{\color{#3a9a38}{1{,}5}\times \color{#3a9a38}{1{,}82} \times \color{#3a9a38}8}{2}|| -
Isoler l’inconnue
||\begin{align} 15{,}42&=1{,}5b+\dfrac{21{,}84}{2}\\15{,}42&=1{,}5b+10{,}92\\15{,}42\color{#ec0000}{-10{,}92}&=1{,}5b+10{,}92\color{#ec0000}{-10{,}92}\\4{,}5&=1{,}5b\\\color{#ec0000}{\dfrac{\color{black}{4{,}5}}{1{,}5}}&=\color{#ec0000}{\dfrac{\color{black}{1{,}5b}}{1{,}5}}\\3&=b \end{align}|| -
Répondre à la question
Pour obtenir la longueur du contour sur laquelle il y aura des lumières, il faut déterminer le périmètre de la figure, c’est-à-dire additionner la mesure de chacun de ses côtés.||\begin{align}\text{Périmètre} &= 8 \times 1{,}5 + 2 \times 3 \\ &= 18\ \text{dm} \\ &= 180\ \text{cm}\end{align}||
Comme on veut installer une lumière tous les |5\ \text{cm},| on peut en installer |36,| car |180 \div 5 = 36.|
Remarque : Il ne faut pas inclure le côté commun au rectangle et à l’octogone dans le périmètre puisqu’il ne fait pas partie du contour de la figure.
Pour valider ta compréhension des mesures manquantes dans les figures planes de façon interactive, consulte la MiniRécup suivante.
