On doit souvent trouver des mesures manquantes dans des figures planes. Parfois, la résolution de tels problèmes crée une équation de degré 2 ou un système d’équations. Pour le résoudre, on doit utiliser la formule quadratique ou bien la factorisation. Il faut aussi connaitre les formules permettant de calculer le périmètre et l’aire. Voici les étapes à suivre pour y arriver.
-
Construire une équation ou un système d'équations à partir du contexte.
-
Résoudre l’équation ou le système d’équations.
-
Répondre à la question.
Voici une série d’exemples. Les premiers sont des problèmes de géométrie qui ne proviennent pas d’un contexte particulier, tandis que le dernier est un problème écrit qui présente une courte mise en situation.
Détermine la mesure de chaque côté du triangle isocèle suivant sachant qu’il a un périmètre de |100\ \text{cm}.|
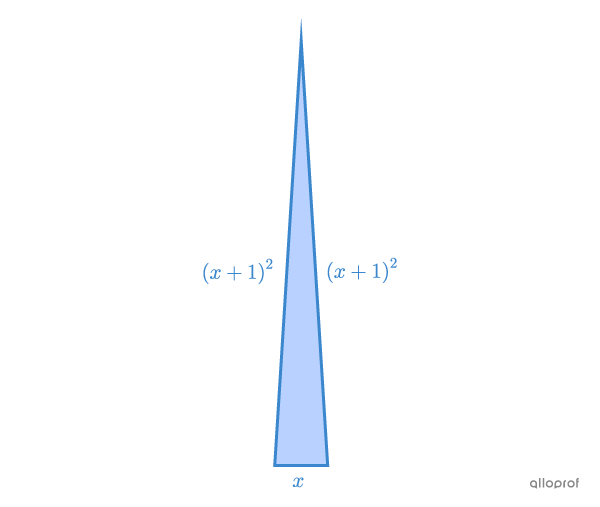
-
Construire une équation à partir du contexte
On utilise la formule du périmètre d’un triangle.||\begin{align}P&= \text{Somme de tous les côtés} \\ 100 &= x + (x+1)^2 + (x+1)^2 \\ 100 &= x + x^2+2x + 1 +x^2 + 2x + 1\\ 100 &= 2x^2 +5x+2 \end{align}||
-
Résoudre l'équation
Comme il s’agit d’une équation de degré 2, on met tous les termes du même côté de l’égalité pour pouvoir la résoudre à l’aide de la formule quadratique.||\begin{align}100&=2x^2+5x+2\\0&=2x^2+5x-98\\\\x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(5)\pm\sqrt{(5)^2-4(2)(-98)}}{2(2)} \\&=\dfrac{-5\pm\sqrt{809}}{4}\end{align}\\\begin{aligned}\\x_1&=\dfrac{-5-\sqrt{809}}{4}&x_2&=\dfrac{-5+\sqrt{809}}{4}\\x_1&\approx-8{,}36&x_2&\approx5{,}86\end{aligned}||Puisqu’on cherche une longueur, on rejette |x_1\approx-8{,}36,| car sa valeur est négative. Ainsi, on a |x\approx5{,}86\ \text{cm}.|
-
Répondre à la question
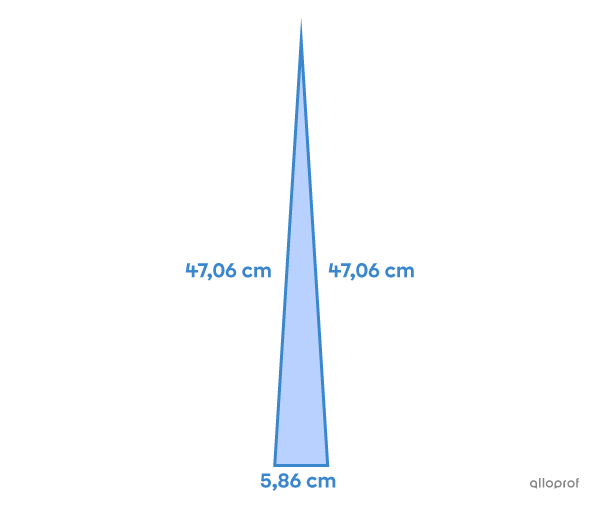
La mesure des côtés isométriques est d’environ |47{,}06\ \text{cm},| car |(x+1)^2 = (5{,}86+1)^2 \approx 47{,}06.| La mesure du 3e côté est d'environ |5{,}86\ \text{cm},| car |x\approx 5{,}86.|
Trouve la mesure des côtés du rectangle suivant sachant que son aire est de |15\ \text{m}^2.|
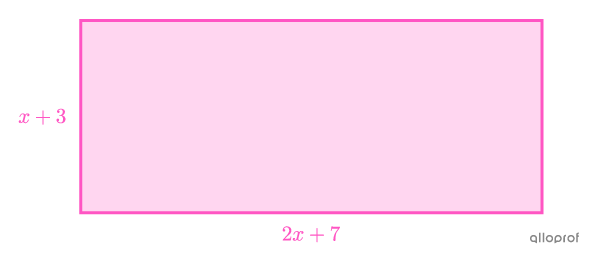
-
Construire une équation à partir du contexte
On utilise la formule de l’aire d’un rectangle.||\begin{align}A&=b\times h \\ 15&=(2x+7)(x+3)\\ 15&=2x^2+6x+7x+21\\ 15&=2x^2+13x+21\end{align}|| -
Résoudre l'équation
Comme il s’agit d’une équation de degré 2, on met tous les termes du même côté pour pouvoir la résoudre. On peut utiliser la technique du produit-somme pour y arriver.||\begin{align}15&=2x^2+13x+21\\0&=2x^2+13x+6\end{align}||On cherche 2 nombres dont le produit est |2\times 6 = 12| et dont la somme est |13.| Ces nombres sont |1| et |12.|||\begin{align}0&=2x^2+\color{#3a9a38}{13x}+6\\0&=2x^2+\color{#3a9a38}{x+12x}+6\\ 0&=x(2x+1)+6(2x+1)\\ 0&=(2x+1)(x+6) \end{align}\\ \begin{aligned}\\0&=2x+1&0&=x+6\\-1&=2x&-6&=x_2\\-0{,}5&=x_1\end{aligned}||On doit rejeter |x_2=-6,| car cette valeur de |x| impliquerait que la mesure des côtés du rectangle soit négative, ce qui est impossible.
-
Répondre à la question
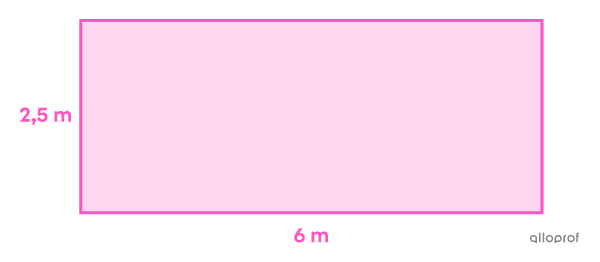
La longueur est de |6\ \text{m},| car |2x+7=2(-0{,}5)+7 =6.| La largeur est de |2{,}5\ \text{m},| car |x+3=-0{,}5+3 =2{,}5.|
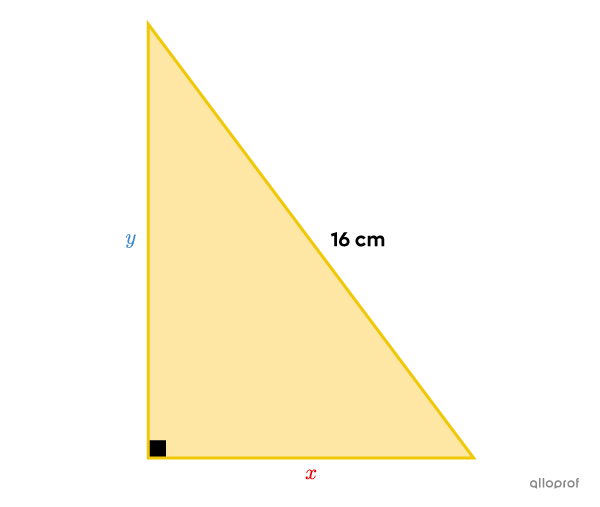
Quelle est la mesure des cathètes du triangle rectangle suivant sachant que son périmètre est de |38{,}4\ \text{cm}| et que son aire est de |61{,}44\ \text{cm}^2?|
-
Construire un système d'équations à partir du contexte
Comme on a 2 inconnues, on doit faire 2 équations. Pour y arriver, on utilise le périmètre et l’aire du triangle.
||\begin{align} P&= \text{Somme de tous les côtés}\\ 38{,}4&= \color{#ec0000}x + \color{#3b87cd}{y}+16 \\22{,}4&= x + y\end{align}||
||\begin{align} A&= \dfrac{\color{#ec0000}b\times \color{#3b87cd}h}{2}\\61{,}44&= \dfrac{\color{#ec0000}x \times \color{#3b87cd}{y}}{2} \\122{,}88&= x\times y\end{align}||
-
Résoudre le système d’équations
On peut isoler |y| dans la 1re équation et le substituer dans la 2e équation.||\begin{align} 22{,}4&=x+y\\22{,}4-x&=y\\\\122{,}88&=x\times \color{#ec0000}y\\122{,}88&=x\times \color{#ec0000}{(22{,}4-x)}\\122{,}88&=22{,}4x-x^2\\ 0&=-x^2+22{,}4x-122{,}88\end{align}||Comme il s’agit d’une équation de degré 2, on utilise la formule quadratique pour la résoudre.||\begin{align}x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(22{,}4) \pm \sqrt{(22{,}4)^2-4(-1)(-122{,}88)}}{2(-1)}\\&=\dfrac{-22{,}4\pm \sqrt{10{,}24}}{-2}\end{align}\\\begin{aligned}\\x_1&=\dfrac{-22{,}4- \sqrt{10{,}24}}{-2}& x_2&=\dfrac{-22{,}4+ \sqrt{10{,}24}}{-2}\\ &= 12{,}8 &&= 9{,}6\end{aligned}||Les 2 valeurs sont valides. Elles représentent respectivement la mesure des cathètes. On suppose que |x| est la petite cathète, alors |x=9{,}6\ \text{cm}| et |y=12{,}8\ \text{cm}.|
-
Répondre à la question
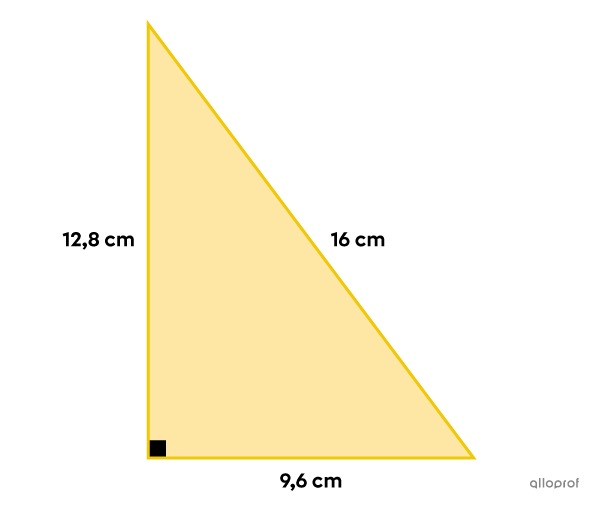
La petite cathète mesure |9{,}6\ \text{cm}| et la grande cathète mesure |12{,}8\ \text{cm}.|
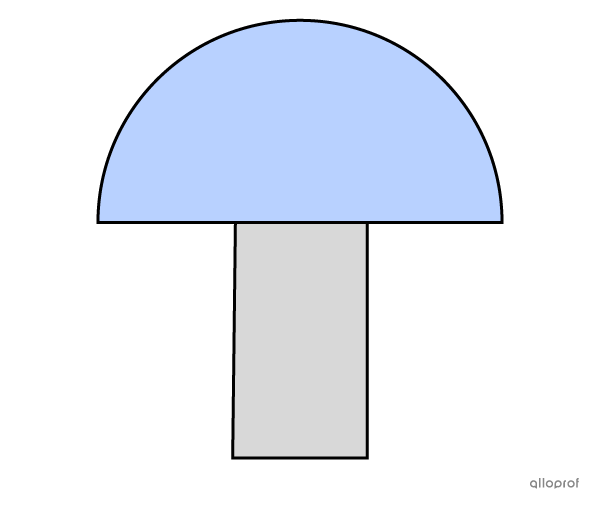
Détermine la hauteur totale de cette figure à l’aide des informations suivantes.
-
La hauteur du rectangle mesure |3\ \text{dm}| de plus que sa base.
-
La mesure du diamètre du demi-disque équivaut au triple de la mesure de la base du rectangle.
-
L'aire totale de cette figure est de |84{,}55\ \text{dm}^2.|
-
Construire une équation à partir du contexte
Puisqu’il n’y a aucune information sur la base du rectangle, on lui associe la variable |x.|
|x :| base du rectangle
La hauteur est de |3\ \text{dm}| de plus que la base, donc l’expression algébrique qui la représente est |x+3.|
Le diamètre du demi-disque est le triple de la base du rectangle, donc l’expression algébrique qui le représente est |3x.|
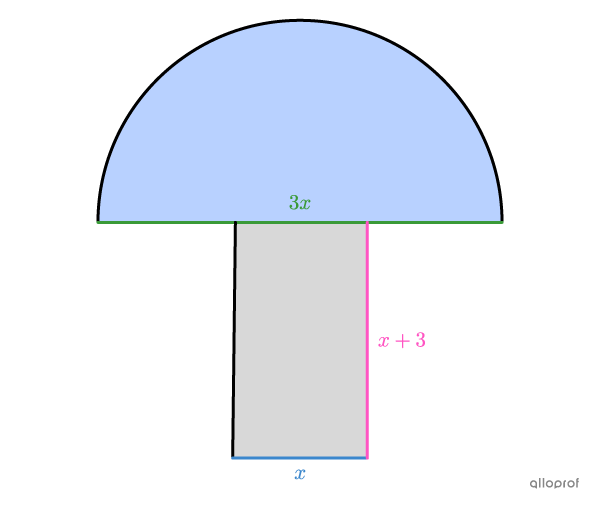
On utilise l’aire totale d’une figure décomposable pour construire l’équation. La figure est composée d’un demi-disque et d’un rectangle. On trouve ainsi l’équation suivante.||\begin{align} A_\text{totale} &= A_\text{rectangle} + A_\text{demi-disque}\\A_\text{totale} &= bh + \dfrac{\pi r^2}{2}\\ 84{,}55 &=\color{#3b87cd}x (\color{#ff55c3}{x+3}) + \dfrac{\pi \left(\dfrac{\color{#3a9a38}{3x}}{2}\right)^2}{2}\\ 84{,}55 &\approx x^2+3x+3{,}53x^2\\84{,}55&\approx4{,}53x^2+3x \end{align}||
-
Résoudre l’équation
Comme il s’agit d’une équation de degré 2, on met tous les termes du même côté pour pouvoir la résoudre à l’aide de la formule quadratique.||\begin{align}84{,}55&\approx4{,}53x^2+3x\\ 0&\approx4{,}53x^2+3x-84{,}55\\\\x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(3) \pm \sqrt{(3)^2-4(4{,}53)(-84{,}55)}}{2(4{,}53)}\\&=\dfrac{-3\pm \sqrt{1\ 541{,}046}}{9{,}06}\end{align}\\ \begin{aligned}\\x_1&=\dfrac{-3- \sqrt{1\ 541{,}046}}{9{,}06}& x_2&=\dfrac{-3+ \sqrt{1\ 541{,}046}}{9{,}06}\\ &\approx -4{,}66 &&\approx 4\end{aligned}||Puisqu'on cherche une longueur, on rejette |x_1\approx-4{,}66,| car la valeur est négative. Ainsi, on a |x\approx 4\ \text{dm}.|
-
Répondre à la question
La hauteur totale de la figure se trouve à l’aide de la hauteur du rectangle et du rayon du demi-disque.||\begin{align}\begin{aligned}\color{#ff55c3}{h_{\text{rectangle}}}&=x+3\\[10pt]&=4+3\\[10pt]&=7\ \text{dm}\\[-2pt]\\ \end{aligned}\quad \begin{aligned}\color{#3a9a38}{r_{\text{demi-disque}}}&=\dfrac{3x}{2}\\&=\dfrac{3(4)}{2}\\&=\dfrac{12}{2}\\&=6\ \text{dm}\end{aligned}\end{align}|| ||\begin{align}h_{\text{totale}}&=\color{#ff55c3}{h_{\text{rectangle}}}+\color{#3a9a38}{r_{\text{demi-disque}}}\\&=7\ \text{dm}+6\ \text{dm}\\&=13\ \text{dm}\end{align}||La hauteur de la figure est de |13\ \text{dm}.|

Avec l'ouverture de son nouveau commerce, le propriétaire d’une crèmerie veut acheter une affiche publicitaire.
Par contre, son budget le limite aux contraintes suivantes.
-
L'aire du demi-disque et du rebord formant la crème glacée doit être égale à |253\ \text{cm}^2.|
-
La superficie du dessin représentant le cornet et le rebord de la crème glacée doit être équivalente à |276\ \text{cm}^2.|
-
La hauteur du cornet doit être de |18\ \text{cm}.|
-
La hauteur du rebord doit être de |4\ \text{cm}.|
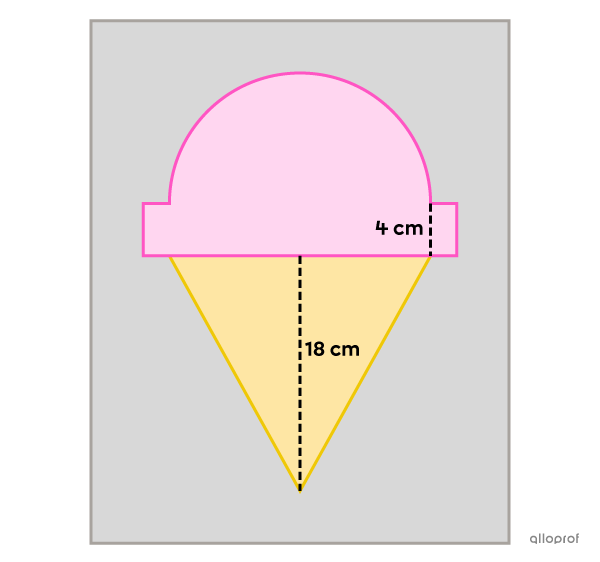
Quelles doivent être les dimensions de l'affiche si on veut que cette dernière dépasse de |4\ \text{cm}| chaque extrémité du dessin?
-
Construire un système d’équations à partir du contexte
Pour déterminer les dimensions de l’affiche, il faut trouver la longueur du rebord ainsi que le rayon du demi-disque.
|x :| Rayon du demi-disque
|y :| Longueur du rebord
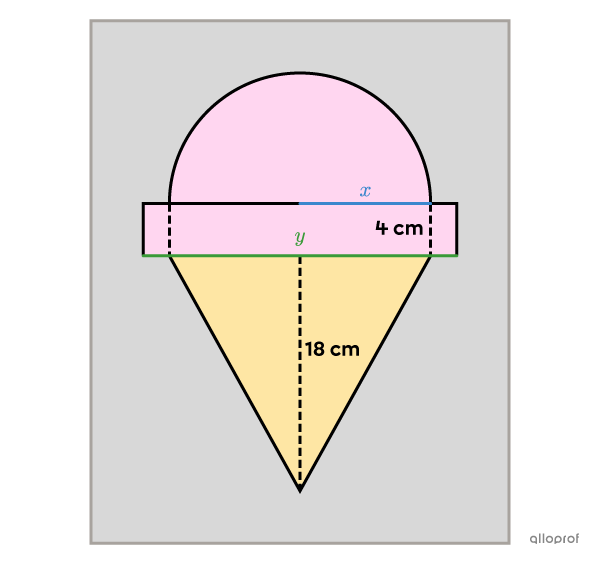
Puisqu’on a 2 informations à propos de l’aire, il est possible de former 2 équations.
||\begin{align}253&=A_{\text{demi-disque}}+A_{\text{rebord}}\\ 253&=\dfrac{\pi\color{#3b87cd}x^2}{2}+4\color{#3a9a38}y\\506&=\pi x^2+8y\end{align}||
||\begin{align}276&=A_{\text{triangle}}+A_{\text{rebord}}\\276&=\dfrac{2\color{#3b87cd}x\times 18}{2}+4\color{#3a9a38}y\\276&=18x+4y\end{align}||
-
Résoudre le système d'équations
Pour résoudre ce système d’équations, on peut multiplier la 2e équation par |2| et faire une réduction.||\begin{align}\color{#ec0000}{2\times \big(}276&=18x+4y\color{#ec0000}{\big)}\\552&=36x+8y\end{align}||On soustrait la 2e équation de la 1re.||\begin{align}506&=\pi x^2\ \ \phantom{+36x} +8y\\ -\ (552&=\ \ \phantom{\pi x^2+} 36x+8y)\\\hline-46&=\pi x^2-36x+0y\end{align}||On utilise la formule quadratique pour résoudre cette équation de degré 2.
||\begin{align}-46&=\pi x^2-36x\\ 0&=\pi x^2-36x+46\\\\x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(-36) \pm \sqrt{(-36)^2-4(\pi)(46)}}{2\pi}\\&\approx\dfrac{36\pm \sqrt{717{,}95}}{6{,}28}\end{align}\\\begin{aligned}\\x_1&\approx\dfrac{36- \sqrt{717{,}95}}{6{,}28}& x_2&\approx\dfrac{36+ \sqrt{717{,}95}}{6{,}28}\\ &\approx 1{,}47 &&\approx 10\end{aligned}||
Les 2 réponses trouvées répondent aux critères. Pour la suite du problème, on choisit |\color{#3b87cd}{x_2 \approx 10}| pour que l’allure du cornet soit plus réaliste. On peut ensuite déterminer la valeur de |y| en remplaçant |x| par |10| dans une des équations précédentes.||\begin{align}276 &= 18\color{#3b87cd}x + 4y\\ 276 &= 18(\color{#3b87cd}{10}) + 4y \\276&=180+4y\\96&=4y\\ 24&=y\end{align}||
-
Répondre à la question
Il ne reste qu’à calculer les dimensions de l’affiche.
Pour la largeur, on utilise |y.|||\begin{align}\text{Largeur}&=4+y+4\\&=4+24+4\\&=32\ \text{cm}\end{align}||Pour la longueur, on utilise |x.|||\begin{align}\text{Longueur}&=4+18+4+x+4\\&=4+18+4+10+4\\&=40\ \text{cm}\end{align}||L’affiche doit avoir une largeur de |32\ \text{cm}| et une longueur de |40\ \text{cm}.|
