Il arrive que l’on cherche des mesures manquantes dans des figures planes. Pour y arriver, il faut résoudre un système d’équations à l’aide de la méthode de comparaison, la méthode de substitution ou la méthode de réduction. Il faut aussi connaitre les formules permettant de calculer le périmètre et l’aire. Voici les étapes à suivre pour y arriver.
-
Construire un système de 2 équations à l’aide des informations fournies dans le problème.
-
Résoudre le système d’équations.
-
Répondre à la question.
Voici une série d’exemples. Les premiers sont des problèmes de géométrie qui ne proviennent pas d’un contexte particulier, tandis que les 2 derniers sont des problèmes écrits qui présentent une courte mise en situation.
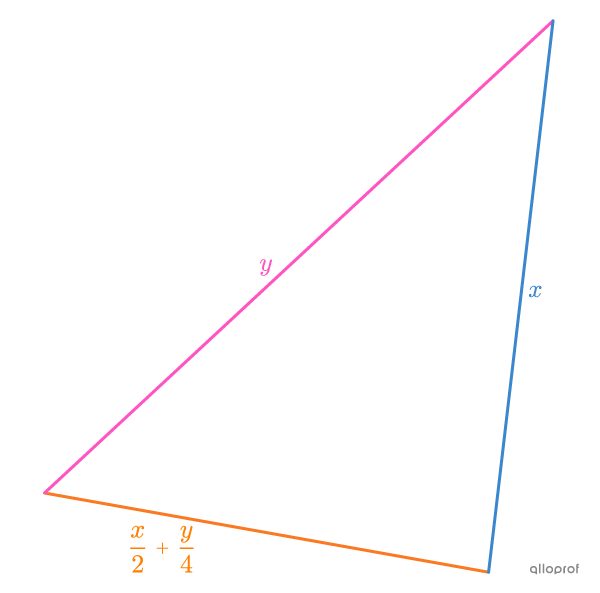
Dans le triangle suivant, |y| représente le côté le plus long, |\dfrac{x}{2}+\dfrac{y}{4}| représente le côté le plus court et |x| représente le 3e côté.
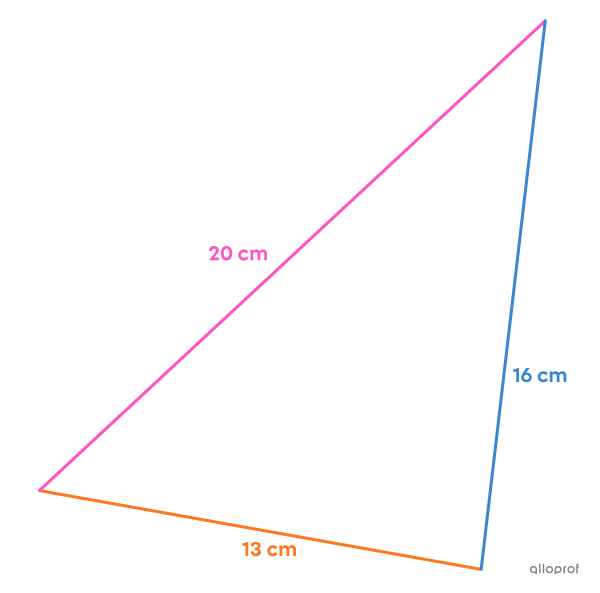
Détermine la mesure de chacun des côtés en sachant que le périmètre du triangle est de |49\ \text{cm}| et que la mesure du côté le plus court est de |13\ \text{cm}.|
-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide du périmètre.||\begin{align}P&=\,\text{Somme de tous les côtés}\\49&=x+y+\dfrac{x}{2}+\dfrac{y}{4}\end{align}||On élimine les fractions en multipliant les 2 membres de l’équation par |4,| puis on réduit.||\begin{align}49\color{#ec0000}{\times4}&=\color{#ec0000}{\left(\color{black}{x+y+\dfrac{x}{2}+\dfrac{y}{4}}\right)\times4}\\196&=4x+4y+2x+y\\196&=6x+5y\end{align}||
2e équation
La 2e équation se construit à l’aide de l’information sur le côté court.||\begin{align} 13&=\text{Mesure du côté court}\\ 13&=\dfrac{x}{2}+\dfrac{y}{4}\end{align}||On élimine les fractions en multipliant les 2 membres de l’équation par |4.|||\begin{align}
13\color{#ec0000}{\times4}&=\color{#ec0000}{\left(\color{black}{\dfrac{x}{2}+\dfrac{y}{4}}\right)\times4}\\
52&=2x+y\end{align}||
-
Résoudre le système d'équations
Il est possible d’utiliser la méthode de réduction pour résoudre ce système d’équation. On commence par multiplier la 2e équation par |3| pour que le coefficient de |x| soit le même dans les 2 équations.||\begin{align}\color{#ec0000}{3\times \big(}52&=2x+y\color{#ec0000}{\big)}\\156&=6x+3y\end{align}||On soustrait la 2e équation de la 1re.||\begin{align}196&=6x+5y\\ -\ (156&=6x+3y)\\\hline40&=0x+2y\end{align}||On résout la nouvelle équation ainsi obtenue.||\begin{align}40&=2y\\20&=y\end{align}||En substituant |y| par |20| dans une des 2 équations, on trouve la valeur de |x.|||\begin{align}52&=2x+\color{#3a9a38}y\\ 52&=2x+\color{#3a9a38}{20}\\ 32&=2x\\ 16&= x\end{align}||
-
Répondre à la question
Ainsi, la mesure du grand côté est de |20\ \text{cm}.|
Pour trouver la mesure du petit côté, on remplace |x| par |16| et |y| par |20| dans l’expression algébrique.||\begin{align}\text{Petit côté}&=\dfrac{\color{#3a9a38}x}{2}+\dfrac{\color{#3a9a38}y}{4}\\&=\dfrac{\color{#3a9a38}{16}}{2}+\dfrac{\color{#3a9a38}{20}}{4}\\&=8+5\\&=13\ \text{cm}\end{align}||
La mesure du 3e côté est de |16\ \text{cm.}|
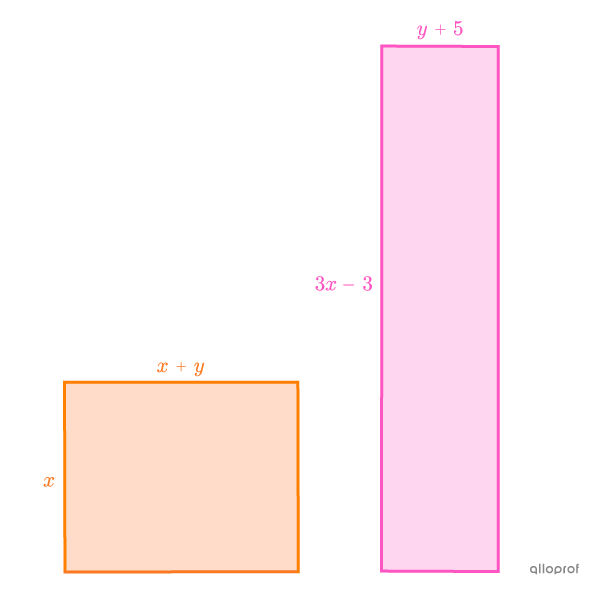
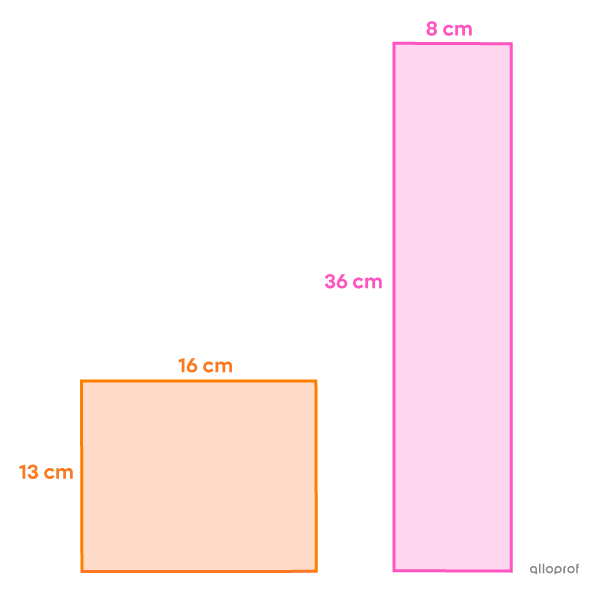
Quelle est la mesure de chacun des côtés des 2 rectangles suivants sachant qu'ils ont des périmètres respectifs de |58\ \text{cm}| et de |88\ \text{cm}|?
-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide du périmètre du 1er rectangle. ||\begin{align}P&=\text{Somme de tous les côtés}\\ 58 &= x + x + (x+y) + (x+y) \\ 58 &= 4x +2y\end{align}||
2e équation
La 2e équation se construit à l’aide du périmètre du 2e rectangle.||\begin{align}P&= \text{Somme de tous les côtés}\\ 88 &= (3x-3)+(3x-3)+(y+5)+(y+5)\\88 &= 6x + 2y +4 \\84&= 6x+2y\end{align}||
-
Résoudre le système d'équations
On peut utiliser la méthode de comparaison pour résoudre ce système d’équation. Pour y arriver, on doit isoler |y| dans les 2 équations.
||\begin{align}58 &= 4x +2y\\58-4x&=2y\\29-2x&=y\end{align}||
||\begin{align}84&= 6x+2y\\84-6x&=2y\\42-3x&=y\end{align}||
On peut ensuite faire la comparaison et résoudre l’équation.||\begin{align}y&=y\\29-2x&=42-3x\\x&=13\end{align}||En substituant |x| par |13| dans une des 2 équations de départ, on trouve la valeur de |y.|||\begin{align}58&=4\color{#3a9a38}x+2y\\ 58&=4\color{#3a9a38}{(13)}+2y\\58&=52+2y\\ 6&=2y&\\ 3&=y\end{align}||
-
Répondre à la question
Ainsi, voici la mesure de chacun des côtés des 2 rectangles.
Largeur du 1er rectangle : |x=13\ \text{cm}|
Longueur du 1er rectangle : |x+y=13+3=16\ \text{cm}|
Largeur du 2e rectangle : |3x-3=3(13)-3=36\ \text{cm}|
Longueur du 2e rectangle : |y+5=3+5=8\ \text{cm}|
Combien mesurent les diagonales des 2 losanges suivants sachant qu'ils ont des aires respectives de |17{,}28\ \text{cm}^2| et |17{,}2\ \text{cm}^2|?

-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide du 1er losange.||\begin{align}A &=\dfrac{D \times d}{2}\\ 17{,}28&=\dfrac{6 (y-x)}{2}\\ 17{,}28&=3y-3x\end{align}||
2e équation
La 2e équation se construit à l’aide du 2e losange.||\begin{align}A&=\dfrac{D \times d}{2}\\ 17{,}2&=\dfrac{(x+y)\times 4}{2}\\ 17{,}2&= 2x + 2y\end{align}||
-
Résoudre le système d'équations
On peut utiliser la méthode de comparaison pour résoudre ce système d’équation. Pour y arriver, on doit isoler |y| dans les 2 équations.
||\begin{align}17{,}28&=3y-3x\\17{,}28+3x&=3y\\5{,}76+x&=y\end{align}||
||\begin{align}17{,}2&= 2x + 2y\\17{,}2-2x&=2y\\8{,}6-x&=y\end{align}||
On peut ensuite faire la comparaison et résoudre l’équation.||\begin{align}\color{#3b87cd}{y}&=\color{#ff55c3}{y}\\ \color{#3b87cd}{5{,}76+x}&=\color{#ff55c3}{8{,}6 - x}\\ 2x &= 2{,}84\\ x &= 1{,}42\end{align}||En substituant |x| par |1{,}42| dans une des 2 équations de départ, on trouve la valeur de |y.|||\begin{align}17{,}28&=\dfrac{6 (y-\color{#3a9a38}x)}{2}\\17{,}28 &=3(y-\color{#3a9a38}{1{,}42}) \\17{,}28 &=3y-4{,}26\\21{,}54 &= 3y \\7{,}18 &= y\end{align}||
-
Répondre à la question
Ainsi, voici la mesure de chacune des diagonales des losanges.
Petite diagonale du 1er losange : |y-x=7{,}18-1{,}42=5{,}76\ \text{cm}|
Grande diagonale du 1er losange : |6\ \text{cm}|
Petite diagonale du 2e losange : |4\ \text{cm}|
Grande diagonale du 2e losange : |x+y=1{,}42+7{,}18=8{,}6\ \text{cm}|

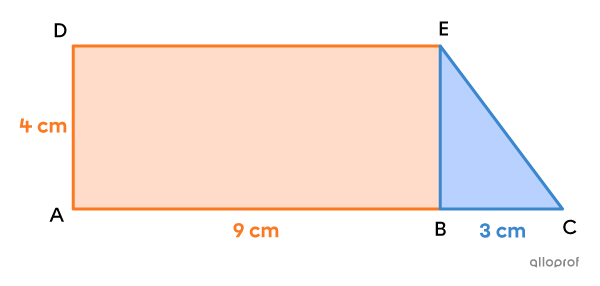
Quelle est la mesure de chacun des côtés du trapèze |\overline{AD},| |\overline{AB}| et |\overline{BC}| sachant que l'aire totale du trapèze est de |42\ \text{cm}^2| et que l'aire de la région triangulaire est de |6\ \text{cm}^2|?

-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide de l’aire du trapèze.||\begin{align}A&=\dfrac{(B+b) \times h}{2}\\ 42&=\dfrac{\big((x+y)+x\big) \times \dfrac{4x}{9}}{2}\\ 42&=\dfrac{(2x+y) \times \dfrac{4x}{9}}{2}\\ 42&=\dfrac{8x^2+4xy}{18}\\ 756 &= 8x^2 +4xy\end{align}||
2e équation
La 2e équation se construit à l’aide de l’aire du triangle.||\begin{align}A&=\dfrac{b \times h}{2}\\6&=\dfrac{y \times \dfrac{4x}{9}}{2}\\ 6&= \dfrac{4xy}{18}\\108&=4xy\end{align}||
-
Résoudre le système d'équations
En utilisant la méthode de substitution, on obtient l’égalité suivante, qu’on résout.||\begin{align}756&=8x^2+\color{#3a9a38}{4xy}\\ 756&=8x^2+ \color{#3a9a38}{108}\\ 648&=8x^2\\ \color{#ec0000}{\sqrt{\color{black}{81}}}&=\color{#ec0000}{\sqrt{\color{black}{x^2}}}\\ \pm\ 9&=x\end{align}||Selon le contexte, on ne conserve que la valeur de |x| positive, car un segment ne peut pas avoir une mesure négative. On substitue donc |x| par |9| dans l’une des équations de départ pour trouver la valeur de |y.|||\begin{align}108&=4xy\\108&=4 \times 9 \times y\\108&=36y\\3&=y\end{align}||
-
Répondre à la question
Voici la longueur des segments.
Longueur de |\overline{AB} :| |x=9\ \text{cm}|
Longueur de |\overline{BC} :| |y=3\ \text{cm}|
Longueur de |\overline{AD} :| |\dfrac{4x}{9}=\dfrac{4(9)}{9}=4\ \text{cm}|
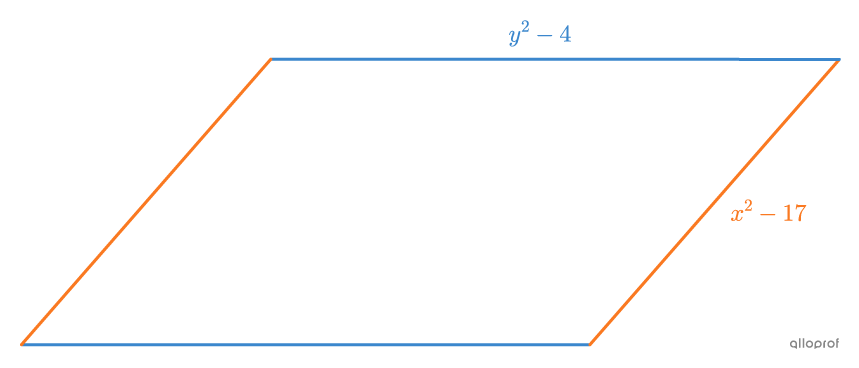
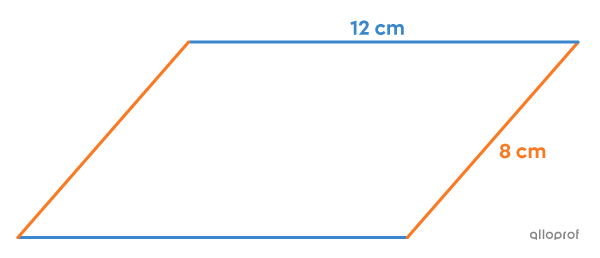
Quelle est la mesure de chacun des côtés du parallélogramme suivant, sachant que son périmètre est de |40\ \text{cm}| et que la mesure du côté le plus court correspond au |\dfrac{2}{3}| de celle du côté le plus long?
-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide du périmètre. ||\begin{align}P&= \text{Somme de tous les côtés} \\40 &=2\left(y^2-4\right) + 2 \left(x^2-17\right)\\ 40&=2y^2-8+2x^2-34 \\82 &= 2x^2+2y^2\end{align}||
2e équation
La 2e équation se construit à l’aide du fait que le côté le plus court correspond au |\dfrac{2}{3}| du plus long.||\begin{align}x^2-17&=\dfrac{2}{3} (y^2-4)\\ 3(x^2-17)&=2(y^2-4)\\ 3x^2-51&=2y^2-8\\-43&=-3x^2+2y^2\end{align}||
-
Résoudre le système d'équations
Comme les coefficients de |y^2| sont identiques dans les 2 équations, on peut utiliser la méthode de réduction.||\begin{align}82&=\ \ \ 2x^2+2y^2\\-\ (-43&=-3x^2+2y^2)\\ \hline 125&=\ \ \ 5x^2+0y^2\end{align}||On résout ensuite la nouvelle équation.||\begin{align}125&=5x^2\\25&=x^2\\\pm 5&=x\end{align}||Pour trouver la valeur de |y,| on utilise l’une des équations de départ. On peut utiliser |5| ou |-5,| la mesure du segment sera la même.||\begin{align}y^2 &= 41-\color{#3a9a38}x^2\\y^2&=41 - (\color{#3a9a38}{\pm\, 5})^2\\y^2&=41-25\\y^2&=16\\y&=\pm 4\end{align}||
-
Répondre à la question
La mesure de la base se détermine de la façon suivante.||\begin{align}y^2-4&=(\pm\, 4)^2-4\\&=16-4\\&=12\ \text{cm}\end{align}||
La mesure des côtés orange se détermine de la façon suivante.||\begin{align}x^2-17&=(\pm\, 5)^2-17\\&=25-17\\&=8\ \text{cm}\end{align}||
Dans un cadre expérimental, une entreprise tente de développer un nouveau type de boomerang. Pour éviter que les gens se blessent, une bande de caoutchouc est installée sur le contour de chaque extrémité.
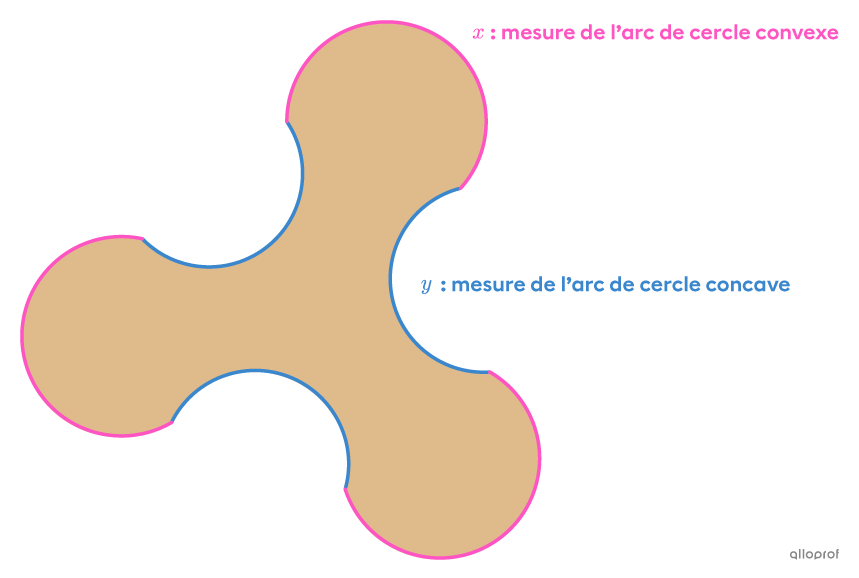
Quelle est la longueur nécessaire de caoutchouc si on sait que :
-
les arcs de cercle de même couleur sont isométriques entre eux;
-
le périmètre du jouet est de |38{,}16\ \text{cm};|
-
un arc de cercle convexe est |1{,}4| fois plus long qu'un arc de cercle concave?
-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide du périmètre.||\begin{align}P&= \text{Somme des arcs de cercle}\\ 38{,}16&= 3x+3y\end{align}||
2e équation
La 2e équation se construit à l’aide du fait qu’un arc de cercle convexe est |1{,}4| fois plus long qu’un arc de cercle concave.||\begin{align}\text{Arc convexe} &= 1{,}4 \times \text{Arc concave}\\ x&=1{,}4y\end{align}||
-
Résoudre le système d'équations
En utilisant la méthode de substitution, on obtient l’égalité suivante, qu’on résout.||\begin{align}38{,}16 &=3\color{#3a9a38}x+3y\\ 38{,}16&=3(\color{#3a9a38}{1{,}4y})+3y\\ 38{,}16&=7{,}2y\\ 5{,}3&= y\end{align}||En remplaçant |y| par |5{,}3| dans l’une des 2 équations de départ, on obtient la valeur de |x.|||\begin{align}x&=1{,}4y\\ x&=1{,}4 (5{,}3)\\ x&= 7{,}42\end{align}||
-
Répondre à la question
Puisqu'il y a 3 arcs convexes, on obtient que la longueur de caoutchouc nécessaire est de |3 \times 7{,}42,| soit |22{,}26\ \text{cm}.|
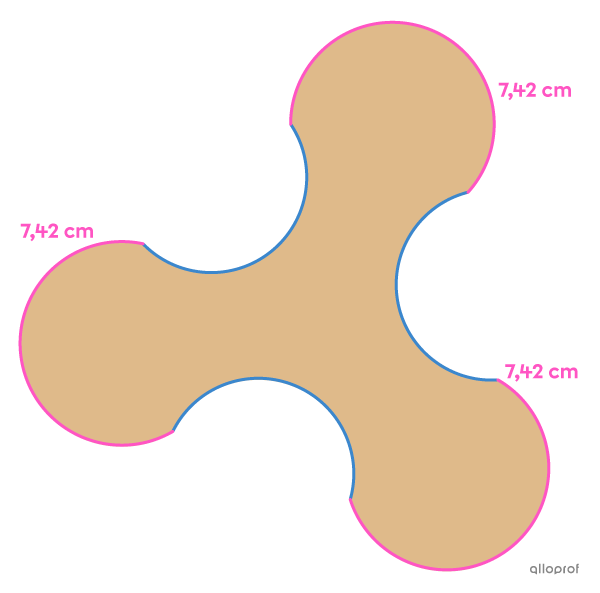
Pour la fête de l'Halloween, un élève décide de porter un costume de ninja. Afin de ne pas déroger aux règlements de l'école, il doit s'assurer que ses accessoires n'excèdent pas une longueur de |10\ \text{cm}.|
Pour ajouter de la vraisemblance à son costume, il décide de se fabriquer un shuriken en carton.

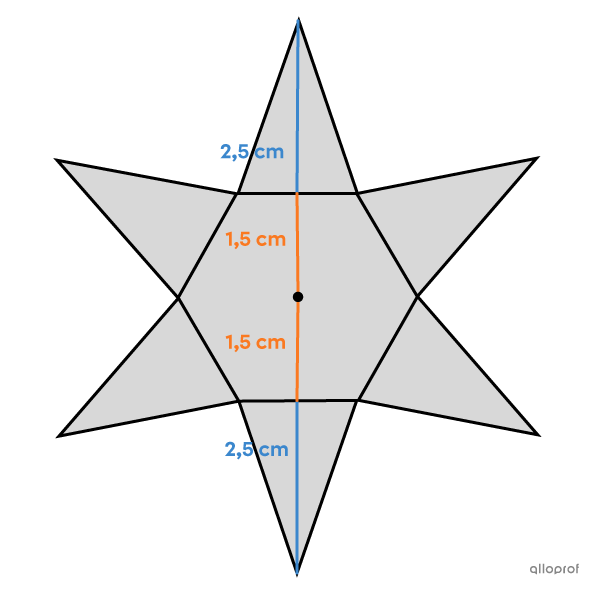
Selon ses calculs, ses étoiles devraient respecter les contraintes suivantes.
-
Chaque étoile est formée d'un hexagone régulier entouré de 6 triangles isocèles isométriques.
-
L'aire totale d'une étoile est de |20{,}74\ \text{cm}^2.|
-
La mesure de la hauteur d'un triangle surpasse celle de l'apothème de |1\ \text{cm}.|
Selon ces informations, est-ce que les étoiles sont conformes aux règlements de l'école?
-
Construire un système de 2 équations
1re équation
La 1re équation se construit à l’aide de l’aire totale d’une étoile.||\begin{align}A_\text{totale}&=A_\text{hexagone}+6\times A_\text{triangles}\\ 20{,}74&=\dfrac{c\times a\times n}{2}+6 \left(\dfrac{b\times h}{2}\right)\\ 20{,}74&=\dfrac{1{,}73 \times x \times 6}{2}+6\left(\dfrac{1{,}73 \times y}{2}\right)\\ 20{,}74&=5{,}19x+5{,}19y\end{align}||
2e équation
La 2e équation se construit à l’aide du fait que la mesure de la hauteur d’un triangle surpasse celle de l’apothème de |1\ \text{cm}.|||y=x+ 1||
-
Résoudre le système d'équations
En utilisant la méthode de substitution, on obtient l’égalité suivante, qu’on résout.||\begin{align}20{,}74&=5{,}19x+5{,}19\color{#3a9a38}{y}\\ 20{,}74&=5{,}19x+5{,}19\color{#3a9a38}{(x+1)}\\ 20{,}74&=5{,}19x+5{,}19x+5{,}19\\ 15{,}55&=10{,}38x\\ 1{,}5&\approx x\end{align}||En remplaçant |x| par |1{,}5| dans la 2e équation, on obtient la valeur de |y.| ||\begin{align}y&=\color{#3a9a38}x+1\\&=\color{#3a9a38}{1{,}5}+1\\&=2{,}5\end{align}||
-
Répondre à la question
Ainsi, il peut apporter ses shuriken, puisque leur longueur est de |2{,}5+1{,}5+1{,}5+2{,}5 = 8\ \text{cm},| ce qui n’excède pas |10\ \text{cm}.|