Le plus petit commun multiple (PPCM) est un multiple qui est commun à deux ou à plusieurs nombres. Des nombres peuvent avoir plus d'un multiple en commun, mais le PPCM ne désigne que le plus petit d'entre eux. Il est toujours différent de 0.
Pour trouver le PPCM à l’aide de la méthode des multiples, je dois suivre les étapes suivantes :
-
J’écris la liste des premiers multiples de chacun des nombres.
-
Je repère les multiples communs à l’ensemble des nombres.
-
J’identifie le plus petit parmi ces multiples.
Quel est le PPCM de 10, 12 et 15?
-
J’écris la liste des premiers multiples de chacun des nombres.

-
Je repère les multiples communs à l’ensemble des nombres.

-
J’identifie le plus petit parmi ces multiples.

Le PPCM de 10, 12 et 15 est 60.
Pour trouver le PPCM à l’aide des facteurs premiers, je dois suivre les étapes suivantes :
-
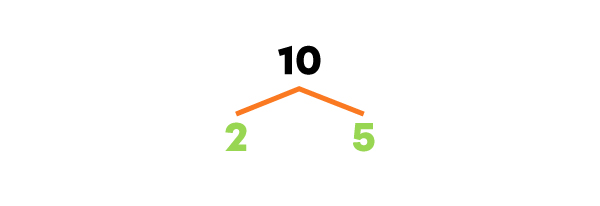
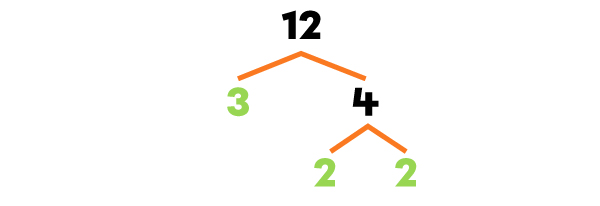
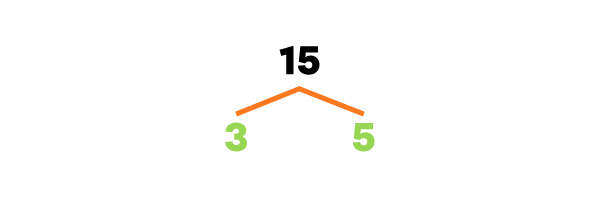
Je fais l’arbre des facteurs de chaque nombre.
-
J’écris les facteurs premiers de chaque nombre.
-
J’identifie les facteurs premiers communs entre au moins deux nombres et je les écris.
-
Je calcule le PPCM en multipliant ensemble les facteurs premiers communs et ceux qui sont seuls.
Quel est le PPCM de 10, 12 et 15?
|
|
|

|
|
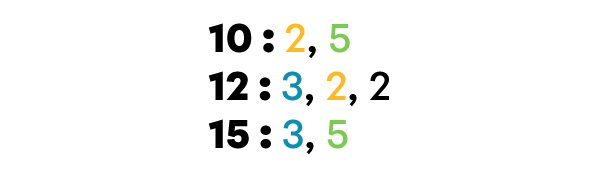
|
|
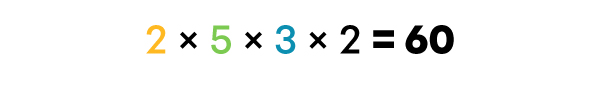
|
Le PPCM de 10, 12 et 15 est 60.
Pour trouver le PPCM à l’aide d’un tableau des diviseurs premiers, je dois suivre les étapes suivantes :
-
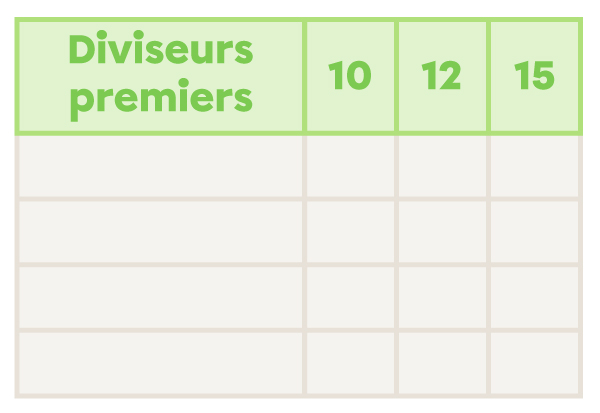
Je trace un tableau dont le titre de la première colonne est Diviseurs premiers. Le titre des autres colonnes correspond aux nombres dont je veux trouver le PPCM.
-
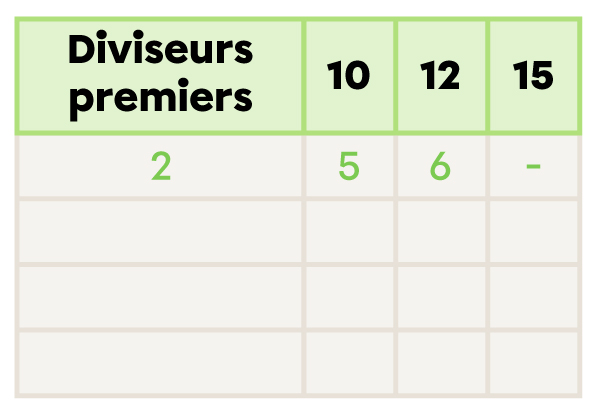
Je tente de diviser les nombres par 2. Si c’est possible, j’écris 2 dans la colonne des diviseurs premiers et la réponse de la division sous chaque nombre.
-
Je recommence jusqu’à ne plus avoir de nombre qui se divise par 2.
-
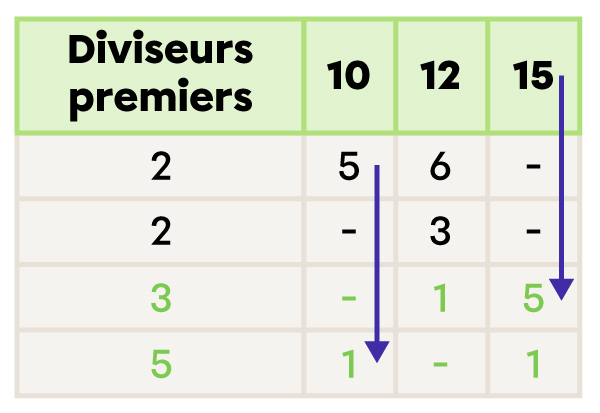
Je tente ensuite de diviser les nombres par 3, puis par 4, 5, 6 et ainsi de suite jusqu’à obtenir 1 dans chaque colonne.
-
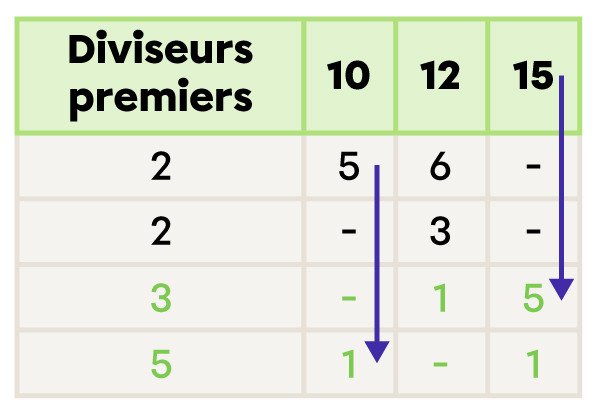
Je calcule le PPCM en multipliant les diviseurs premiers de la première colonne.
Quel est le PPCM de 10, 12 et 15?
|
|
|
|
|
|
|
|
|
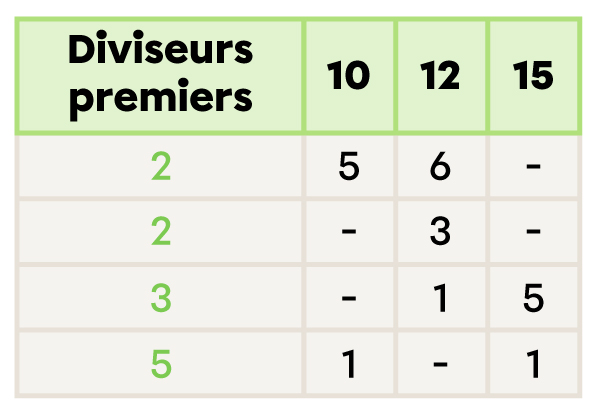
2 × 2 × 3 × 5 = 60 |
Le PPCM de 10, 12 et 15 est 60.