Le théorème de Thalès est très utile lorsqu'on recherche une ou des mesures manquantes dans une figure formée par des sécantes qui croisent des droites parallèles.
Si, dans une figure…
-
… les droites |\color{#3a9a38}{BD}| et |\color{#3b87cd}{CE}| sont sécantes en |A;|
-
… les droites |\color{#ec0000}{BC}| et |\color{#ec0000}{DE}| sont parallèles,
alors, on a la proportion suivante.||\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}}=\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}||
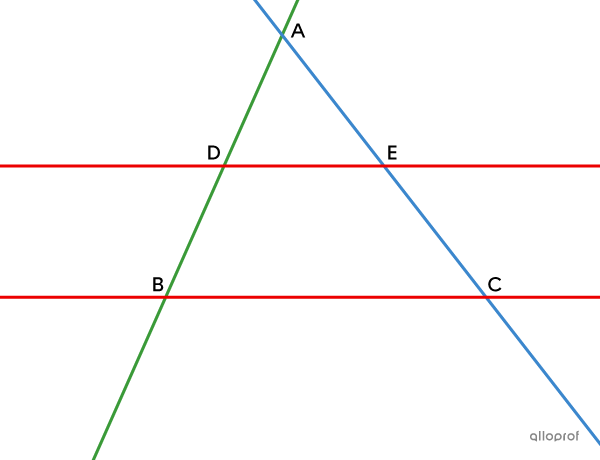
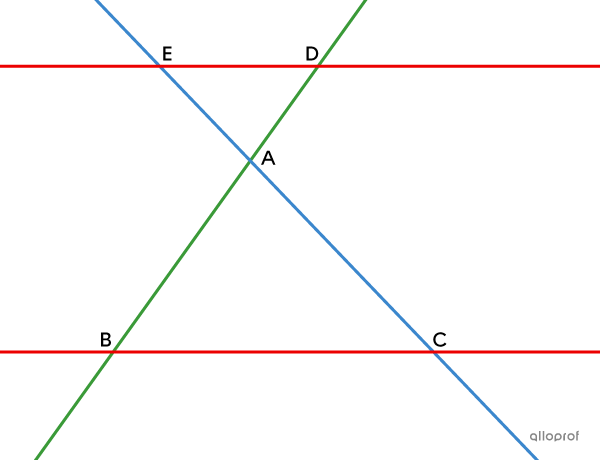
Remarque : Le théorème de Thalès s'applique peu importe si les sécantes |(\color{#3b87cd}{EC}| et |\color{#3a9a38}{BD})| se croisent à l’extérieur ou à l’intérieur des parallèles |(\color{#ec0000}{ED}| et |\color{#ec0000}{BC}).|
Le théorème de Thalès vient de Thalès de Milet, un savant de l’Antiquité qui a vécu vers 600 av. J.-C. Voici la méthode qu’il a utilisée pour calculer la hauteur de certaines pyramides d’Égypte à l’aide de l’ombre qu’elles projettent.
Pour mesurer la hauteur de la pyramide, une personne doit se placer de sorte que son ombre soit alignée sur celle de la pyramide. De cette façon, on obtient 2 triangles semblables. Il suffit ensuite d’établir la bonne proportion et de la résoudre.
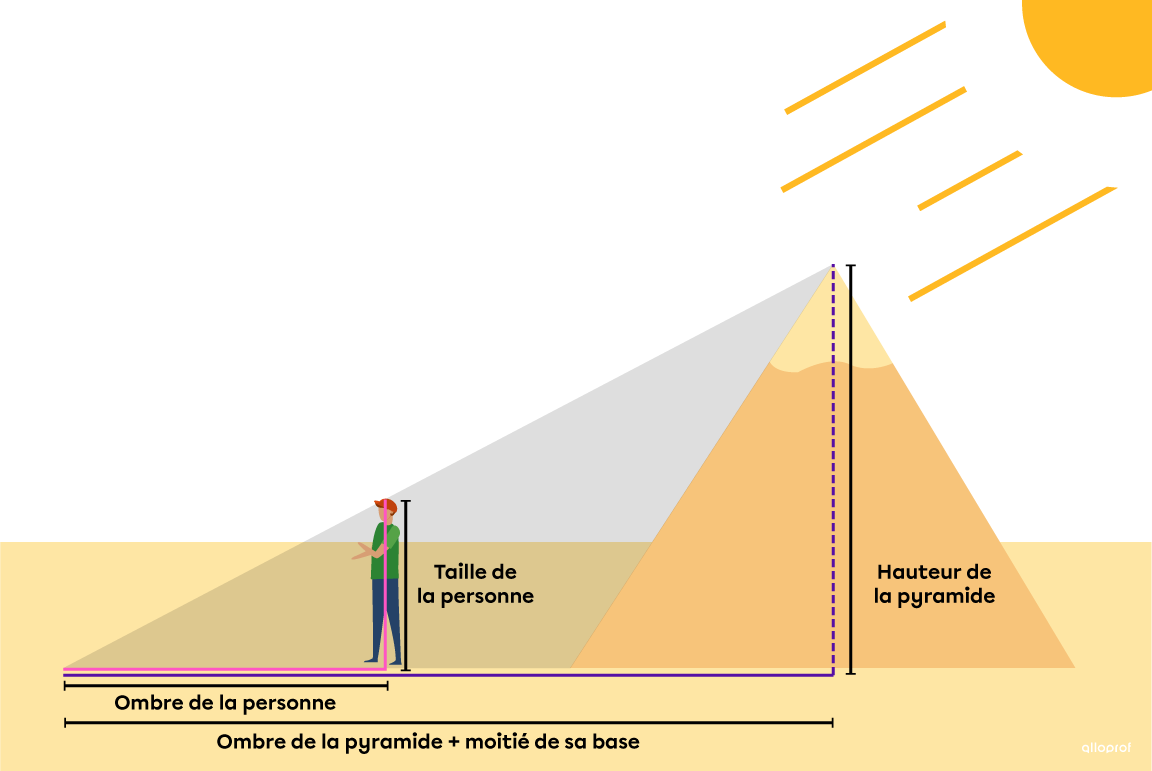
Selon le théorème de Thalès, comme la taille de la personne et la hauteur de la pyramide sont des segments parallèles, on peut appliquer la proportion suivante.||\dfrac{\begin{gather}\text{Taille de}\\\text{la personne}\end{gather}}{\begin{gather}\text{Hauteur de}\\\text{la pyramide}\end{gather}} =\dfrac{\begin{gather}\text{Ombre de}\\\text{la personne}\end{gather}}{\begin{gather}\text{Ombre de la pyramide}\\\text{+ moitié de sa base}\end{gather}}||À l’aide de cette méthode, on peut trouver la hauteur de n’importe quoi, comme la hauteur d’une maison ou d’une école. À toi d’essayer!
Si, dans une figure…
-
… les droites |\color{#3a9a38}{BD}| et |\color{#3b87cd}{CE}| sont sécantes en |A;|
-
… les droites |\color{#ec0000}{BC}| et |\color{#ec0000}{DE}| sont parallèles,
alors, on a la proportion suivante.||\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}}=\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}||
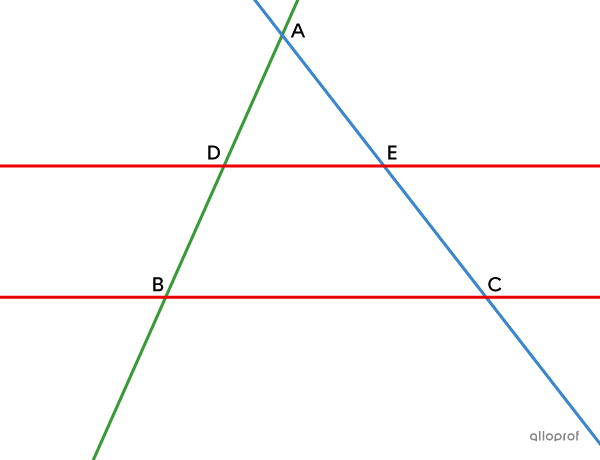
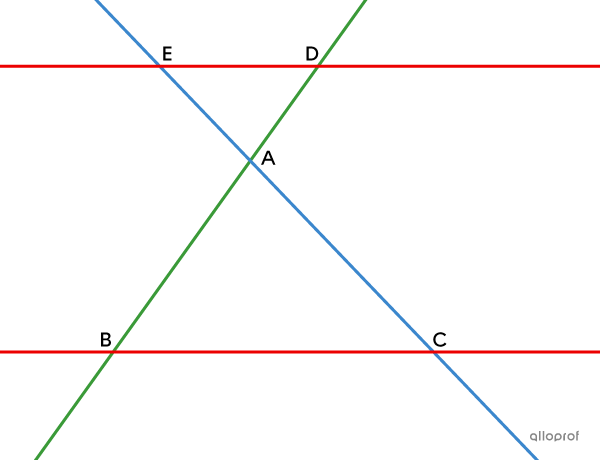
Remarque : Le théorème de Thalès s'applique peu importe si les sécantes |(\color{#3b87cd}{EC}| et |\color{#3a9a38}{BD})| se croisent à l’extérieur ou à l’intérieur des parallèles |(\color{#ec0000}{ED}| et |\color{#ec0000}{BC}).|
Le théorème de Thalès repose sur les proportions des côtés homologues des triangles semblables. On le prouve en démontrant que |\triangle ABC \sim \triangle ADE| à l’aide du cas de similitude AA.
Hypothèses
Soit les droites parallèles distinctes |\color{#ec0000}{BC}| et |\color{#ec0000}{DE},| ainsi que les droites sécantes |\color{#3a9a38}{AB}| et |\color{#3b87cd}{AC}.|
Conclusion
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}||
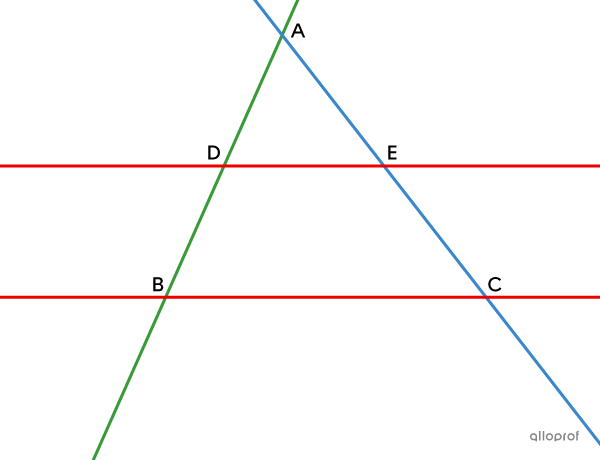
Démonstration
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les angles |DAE| et |BAC| sont isométriques.||\angle DAE\cong\angle BAC|| |
A |
Il s’agit d’un angle commun aux 2 triangles. |
|
2 |
Les angles |ADE| et |ABC| sont isométriques.||\angle ADE\cong\angle ABC|| |
A |
Des parallèles |(\color{#ec0000}{BC}| et |\color{#ec0000}{DE})| coupées par une sécante |(\color{#3a9a38}{AB})| forment des angles correspondants isométriques. |
|
3 |
Les triangles |ABC| et |ADE| sont semblables.||\triangle ABC\sim\triangle ADE|| |
Ils respectent la condition minimale AA : des triangles sont semblables s’ils ont 2 paires d’angles homologues isométriques. |
|
|
4 |
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}|| |
Dans les triangles semblables, les côtés homologues sont proportionnels. |
|
La démonstration du théorème de Thalès dans le cas où le point d’intersection des droites sécantes |(A)| est situé entre les 2 droites parallèles se fait aussi à l’aide de la condition minimale de similitude AA.
Hypothèses
Soit les droites parallèles distinctes |\color{#ec0000}{BC}| et |\color{#ec0000}{DE},| ainsi que les droites sécantes |\color{#3a9a38}{AB}| et |\color{#3b87cd}{AC}.|
Conclusion
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}||
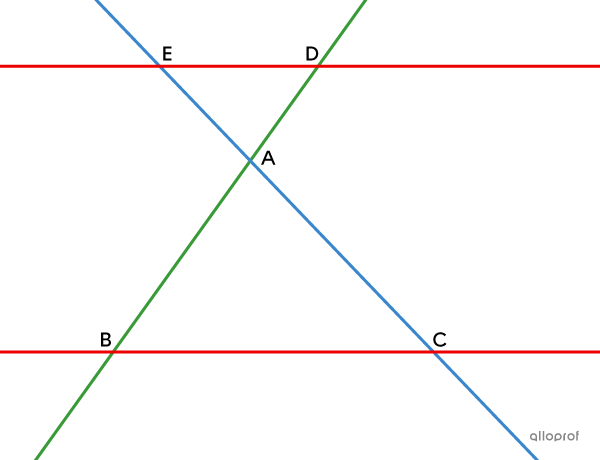
Démonstration
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les angles |DAE| et |BAC| sont isométriques.||\angle DAE\cong\angle BAC|| |
A |
Ce sont des angles opposés par le sommet. |
|
2 |
Les angles |ADE| et |ABC| sont isométriques.||\angle ADE\cong\angle ABC|| |
A |
Des parallèles |(\color{#ec0000}{BC}| et |\color{#ec0000}{DE})| coupées par une sécante |(\color{#3a9a38}{BD})| forment des angles alternes-internes isométriques. |
|
3 |
Les triangles |ABC| et |ADE| sont semblables.||\triangle ABC\sim\triangle ADE|| |
Ils respectent la condition minimale AA : des triangles sont semblables s’ils ont 2 paires d’angles homologues isométriques. |
|
|
4 |
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}|| |
Dans les triangles semblables, les côtés homologues sont proportionnels. |
|
Dès qu’on sait qu’on a 2 droites parallèles coupées par 2 sécantes, on peut utiliser le théorème de Thalès et résoudre la proportion dans les triangles sans avoir à prouver qu’ils sont semblables.
Trouve la mesure manquante, sachant que les droites |\color{#ec0000}{ED}| et |\color{#ec0000}{BC}| sont parallèles.
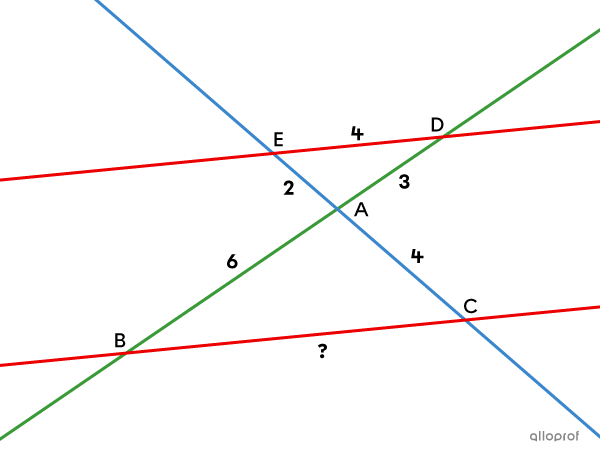
Selon le théorème de Thalès, comme les droites |\color{#ec0000}{ED}| et |\color{#ec0000}{BC}| sont parallèles, on peut appliquer la proportion suivante.||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}= \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}= \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}||Pour trouver |\text{m}\overline{BC},| on utilise l’égalité suivante, qu’on résout.||\begin{align}\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}&= \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}\\ \dfrac{2}{4}&=\dfrac{4}{\text{m}\overline{BC}}\\\\ \text{m}\overline{BC}&=\dfrac{4\times 4}{2}\\&=8\end{align}||Réponse : |\text{m}\overline{BC} = 8\ \text{unités}|
Avec les configurations associées au théorème de Thalès, si les droites sont parallèles, alors on en retire une proportion. Toutefois, il est aussi possible de suivre le raisonnement inverse, c’est-à-dire que si la proportion est vérifiée, alors on en déduit que les droites sont parallèles. C'est ce qu'on appelle la réciproque du théorème de Thalès.
Hypothèses
Les droites |\color{#3a9a38}{BD}| et |\color{#3b87cd}{CE},| sécantes en |A,| sont placées de telle sorte que la proportion suivante est respectée.||\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}} =\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}||
Conclusion
Les droites |\color{#ec0000}{BC}| et |\color{#ec0000}{DE}| sont parallèles.
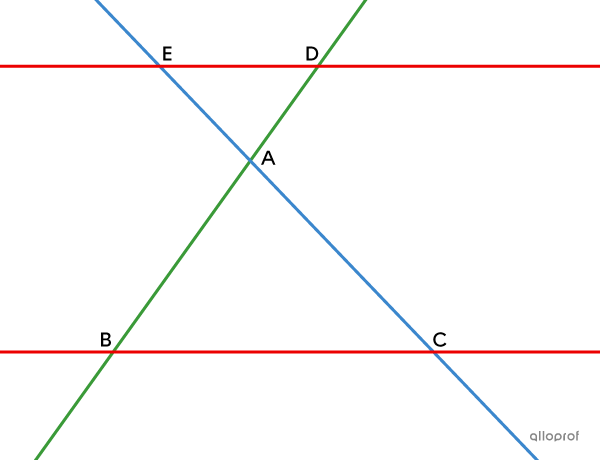
Démonstration
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les triangles |ABC| et |ADE| sont semblables. ||\triangle ABC \sim \triangle ADE|| |
Par hypothèse, les côtés homologues des triangles |ABC| et |ADE| sont proportionnels. Ceux-ci respectent donc la condition minimale CCC : des triangles sont semblables si les mesures de leurs côtés homologues sont proportionnelles. |
|
|
2 |
Les angles |ADE| et |ABC| sont isométriques.||\angle ADE\cong\angle ABC|| |
Dans les triangles semblables, les angles homologues sont isométriques. |
|
|
3 |
Les droites |\color{#ec0000}{BC}| et |\color{#ec0000}{DE}| sont parallèles. ||\color{#ec0000}{BC}\parallel \color{#ec0000}{DE}|| |
Des droites |(\color{#ec0000}{BC}| et |\color{#ec0000}{DE})| coupées par une sécante |(\color{#3a9a38}{BD})| forment des angles alternes-internes isométriques |(\angle ADE| et |\angle ABC)| si et seulement si ces droites sont parallèles. |
|
Sachant que les droites |\color{#3b87cd}{EC}| et |\color{#3a9a38}{BD}| sont sécantes en |A,| démontre que les droites |\color{#ec0000}{ED}| et |\color{#ec0000}{BC}| sont parallèles.
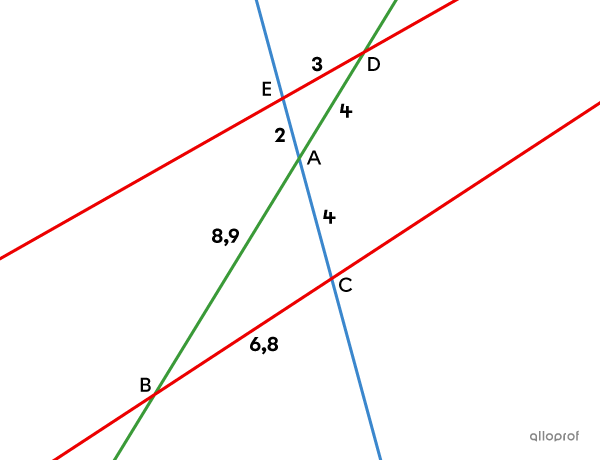
On doit vérifier que la proportion du théorème de Thalès entre les côtés homologues des triangles |ADE| et |ABC| est vraie. Si on montre que les 3 rapports sont équivalents, alors on peut conclure que les droites sont parallèles.||\begin{align}\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}}&=\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}\\ \color{#3a9a38}{\dfrac{4}{8{,}9}}\quad &\neq\quad\color{#3b87cd}{\dfrac{2}{4}}\quad \neq\quad\color{#ec0000}{\dfrac{3}{6{,}8}}\end{align}||Conclusion : Puisque les 3 rapports ne sont pas égaux, les droites |\color{#ec0000}{ED}| et |\color{#ec0000}{BC}| ne sont pas parallèles.
Lorsqu'on a plusieurs droites parallèles interceptées par 2 droites, il est possible d'utiliser ce qu'on appelle le théorème de Thalès généralisé.
Si, dans une figure…
-
… les droites |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| et |\color{#ec0000}{CC’}| sont parallèles;
-
… les points |A,| |B| et |C| sont alignés;
-
… les points |A’,| |B’| et |C’| sont alignés,
alors, on a la proportion suivante.||\dfrac{\color{#3b87cd}{\text{m}\overline{A’B’}}}{\color{#3a9a38}{\text{m}\overline{AB}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{B’C’}}}{\color{#3a9a38}{\text{m}\overline{BC}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{A’C’}}}{\color{#3a9a38}{\text{m}\overline{AC}}}||
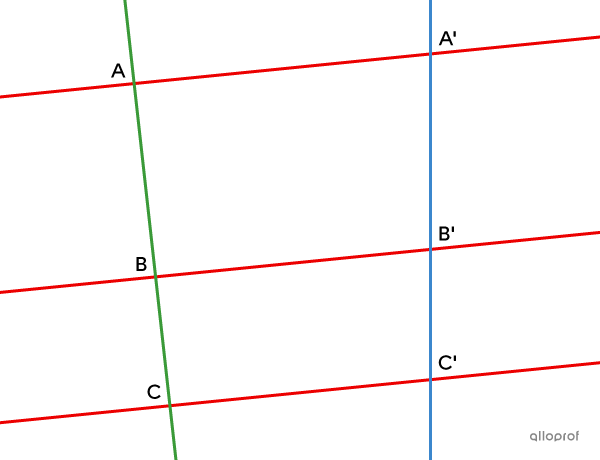
Dans le théorème de Thalès généralisé, on ne peut pas établir une proportion entre les segments situés sur les droites parallèles |(AA’,| |BB’| et |CC’).| ||\dfrac{\text{m}\overline{AA’}}{\text{m}\overline{BB'}}\boldsymbol{\color{#ec0000}\neq} \dfrac{\text{m}\overline{BB’}}{\text{m}\overline{CC'}}\boldsymbol{\color{#ec0000}\neq} \dfrac{\text{m}\overline{AA’}}{\text{m}\overline{CC'}}||
Sachant que les droites |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| et |\color{#ec0000}{CC’}| sont parallèles, trouve |\text{m}\overline{B'C'}.|
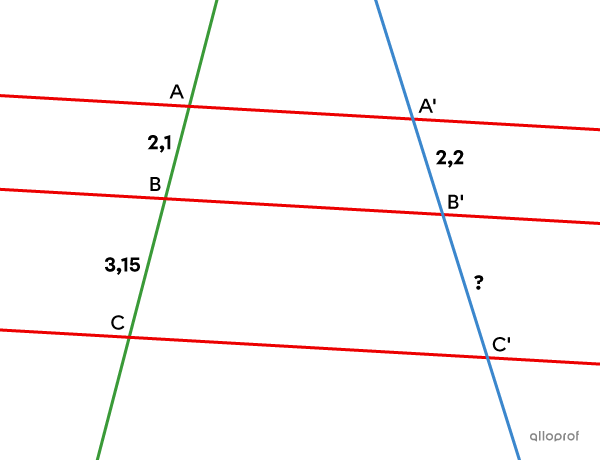
Selon le théorème de Thalès généralisé, comme les droites |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| et |\color{#ec0000}{CC’}| sont parallèles, on peut appliquer la proportion suivante. ||\dfrac{\color{#3b87cd}{\text{m}\overline{A’B’}}}{\color{#3a9a38}{\text{m}\overline{AB}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{B’C’}}}{\color{#3a9a38}{\text{m}\overline{BC}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{A’C’}}}{\color{#3a9a38}{\text{m}\overline{AC}}}||Pour trouver |\text{m}\overline{B’C’},| on utilise l’égalité suivante, qu’on résout. ||\begin{align}\dfrac{\color{#3b87cd}{\text{m}\overline{A'B'}}}{\color{#3a9a38}{\text{m}\overline{AB}}}&= \dfrac{\color{#3b87cd}{\text{m}\overline{B'C'}}}{\color{#3a9a38}{\text{m}\overline{BC}}}\\ \dfrac{\color{#3b87cd}{2{,}2}}{\color{#3a9a38}{2{,}1}}&= \dfrac{\color{#3b87cd}{x}}{\color{#3a9a38}{3{,}15}}\\\\ x&=\dfrac{3{,}15\times 2{,}2}{2{,}1}\\&=3{,}3\end{align}||Réponse : |\text{m}\overline{B’C’}=3{,}3\ \text{unités}|