Lorsqu’on compare des polygones, on peut déterminer qu’il s’agit de figures isométriques en vérifiant s’ils possèdent des angles homologues et des côtés homologues isométriques. C’est la même chose pour les triangles. Heureusement, pour prouver l’isométrie de triangles, il n’est pas nécessaire de connaitre la mesure de tous les côtés et de tous les angles. Il suffit de vérifier que certaines conditions minimales sont respectées. C’est ce qu’on appelle les cas d’isométrie des triangles.
Les conditions minimales d’isométrie des triangles permettent de démontrer que des triangles sont isométriques en utilisant le moins d'arguments possible.
Il existe 3 cas d’isométrie dans les triangles. Il existe aussi des cas de similitude des triangles. On utilise le cas le plus approprié selon les informations fournies dans le problème et on organise notre démarche dans un tableau d’affirmations et de justifications.
On peut expliquer pourquoi les conditions minimales sont suffisantes pour affirmer que des triangles sont isométriques en s’intéressant à la construction des triangles en question.
Des triangles sont isométriques si et seulement si leurs côtés homologues sont isométriques.
La condition CCC (Côté-Côté-Côté) n’implique aucune mesure d’angle. En effet, il suffit de montrer que les 3 paires de côtés homologues ont la même mesure pour conclure que les triangles sont isométriques.
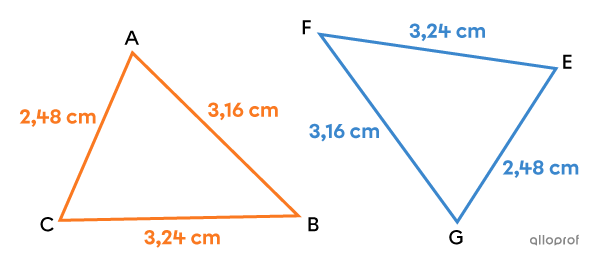
Démontre que les triangles |ABC| et |GFE| suivants sont isométriques.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les segments |\overline{AC}| et |\overline{EG}| sont isométriques.||\overline{AC} \cong\overline{EG}|| |
C |
Par hypothèse. |
|
2 |
Les segments |\overline{AB}| et |\overline{FG}| sont isométriques.||\overline{AB} \cong\overline{FG}|| |
C |
Par hypothèse. |
|
3 |
Les segments |\overline{BC}| et |\overline{EF}| sont isométriques. |
C |
Par hypothèse. |
|
4 |
Les triangles |ABC| et |GFE| sont isométriques. |
Ils respectent la condition minimale CCC : des triangles sont isométriques si et seulement si leurs côtés homologues sont isométriques. |
|
Avant de commencer une démonstration d’isométrie, il est important de bien identifier les paires de côtés homologues. Dans l’exemple précédent, c'est une rotation qui associe les 2 triangles. Les segments |\overline{AC}| et |\overline{GE}| sont homologues, car chaque segment est le plus petit côté de son triangle. On applique le même raisonnement pour les 2 autres paires de côtés homologues.
Des triangles sont isométriques si et seulement s’ils ont une paire d’angles isométriques compris entre 2 paires de côtés homologues isométriques.
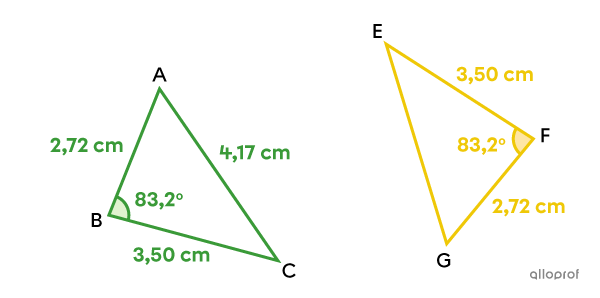
Démontre que les triangles |ABC| et |GFE| suivants sont isométriques.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les segments |\overline{AB}| et |\overline{FG}| sont isométriques.||\overline{AB} \cong\overline{FG}|| |
C |
Par hypothèse. |
|
2 |
Les angles |ABC| et |GFE| sont isométriques.||\angle{ABC} \cong \angle{GFE}|| |
A |
Par hypothèse. |
|
3 |
Les segments |\overline{BC}| et |\overline{EF}| sont isométriques.||\overline{BC} \cong \overline{EF}|| |
C |
Par hypothèse. |
|
4 |
Les triangles |ABC| et |GFE| sont isométriques.||\triangle ABC \cong \triangle GFE|| |
Ils respectent la condition minimale CAC : des triangles sont isométriques s’ils ont une paire d’angles isométriques compris entre 2 paires de côtés homologues isométriques. |
|
L'angle choisi doit être formé par les paires de côtés homologues analysées. Si l'angle n'est pas au bon endroit, les 2 triangles ne sont pas nécessairement isométriques.
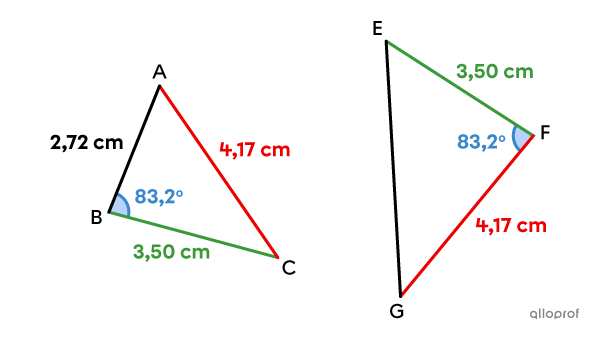
Par exemple, sur l’image ci-dessus, |\angle{ABC}| et |\angle{EFG}| ont la même mesure. Par contre, l’angle |ABC| est situé entres des côtés de |2{,}72| et de |3{,}50\ \text{cm},| tandis que l’angle |EFG| est situé entre des côtés de |4{,}17| et de |3{,}50\ \text{cm}.| Les 2 triangles ne sont donc pas isométriques.||\triangle ABC\color{#ec0000}\not\cong\triangle EFG||
Des triangles sont isométriques si et seulement s’ils ont une paire de côtés isométriques compris entre 2 paires d’angles homologues isométriques.
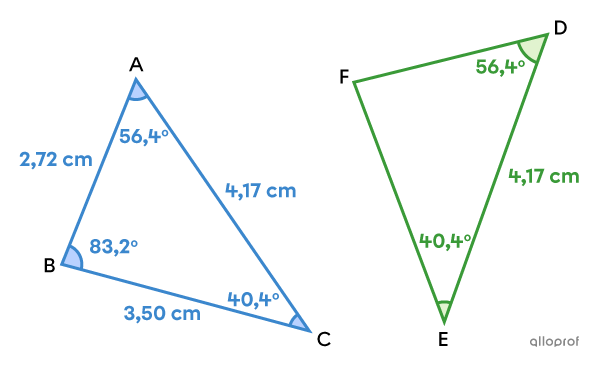
Démontre que les triangles |ABC| et |DFE| suivants sont isométriques.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les angles |BAC| et |EDF| sont isométriques.||\angle{BAC} \cong \angle{EDF}|| |
A |
Par hypothèse. |
|
2 |
Les segments |\overline{AC}| et |\overline{DE}| sont isométriques.||\overline{AC} \cong \overline{DE}|| |
C |
Par hypothèse. |
|
3 |
Les angles |ACB| et |DEF| sont isométriques.||\angle{ACB} \cong \angle{DEF}|| |
A |
Par hypothèse. |
|
4 |
Les triangles |ABC| et |DEF| sont isométriques.||\triangle ABC \cong \triangle DEF|| |
Ils respectent la condition minimale ACA : des triangles sont isométriques s’ils ont une paire de côtés isométriques compris entre 2 paires d’angles homologues isométriques. |
|
La position des paires de côtés homologues et d'angles homologues dans les triangles est essentielle. Si la paire de côtés homologues ne se situe pas entre les 2 paires d'angles homologues, alors les 2 triangles ne sont pas nécessairement isométriques.
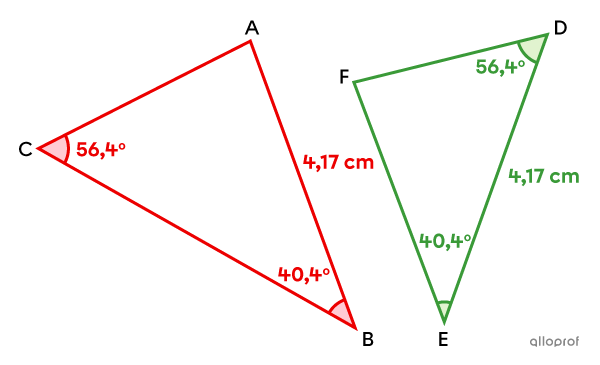
Par exemple, dans le triangle |ABC,| le côté qui mesure |4{,}17\ \text{cm}| n'est pas compris entre les angles de |40{,}4^\circ| et de |56{,}4^\circ,| alors que c'est le cas dans le triangle |DEF.| Les triangles |ABC| et |DEF| ne sont donc pas isométriques.||\triangle ABC\color{#ec0000}\not\cong\triangle DEF||
Il est possible d’utiliser les conditions minimales d’isométrie des triangles ainsi que les propriétés des quadrilatères pour compléter des démonstrations.
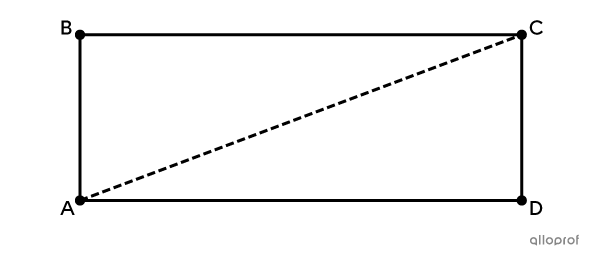
Le quadrilatère |ABCD| suivant est un rectangle.
Démontre que les triangles |ABC| et |CDA| sont isométriques.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les segments |\overline{AB}| et |\overline{CD}| sont isométriques.||\overline{AB} \cong \overline{CD}|| |
C |
Dans un rectangle, les côtés opposés sont isométriques. |
|
2 |
Les angles |ABC| et |CDA| sont isométriques.||\angle{ABC} \cong \angle{CDA}|| |
A |
Dans un rectangle, les 4 angles sont des angles droits. |
|
3 |
Les segments |\overline{BC}| et |\overline{AD}| sont isométriques.||\overline{BC} \cong \overline{AD}|| |
C |
Dans un rectangle, les côtés opposés sont isométriques. |
|
4 |
Les triangles |ABC| et |CDA| sont isométriques.||\triangle ABC \cong \triangle CDA|| |
Ils respectent la condition minimale CAC : des triangles sont isométriques s’ils ont une paire d’angles homologues isométriques compris entre 2 paires de côtés homologues isométriques. |
|
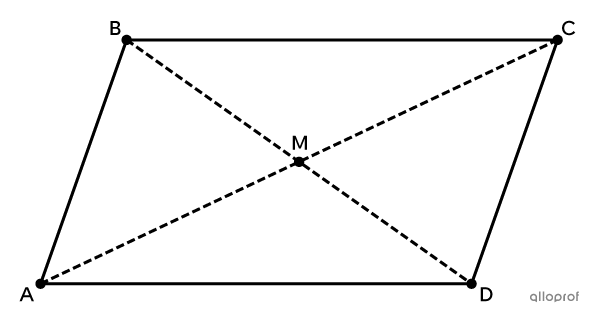
Le quadrilatère |ABCD| suivant est un parallélogramme. |M| est le point d’intersection des 2 diagonales |\overline{BD}| et |\overline{AC}.|
Démontre que les triangles |BCM| et |DAM| sont isométriques.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les segments |\overline{BC}| et |\overline{AD}| sont isométriques.||\overline{BC} \cong\overline{AD}|| |
C |
Dans un parallélogramme, les côtés opposés sont isométriques. |
|
2 |
Les segments |\overline{BM}| et |\overline{DM}| sont isométriques.||\overline{BM} \cong \overline{DM}|| |
C |
Les diagonales d'un parallélogramme se coupent en leur milieu. |
|
3 |
Les segments |\overline{AM}| et |\overline{CM}| sont isométriques.||\overline{AM} \cong \overline{CM}|| |
C |
Les diagonales d'un parallélogramme se coupent en leur milieu. |
|
4 |
Les triangles |BCM| et |DAM| sont isométriques.||\triangle BCM \cong \triangle DAM|| |
Ils respectent la condition minimale CCC : des triangles sont isométriques si leurs côtés homologues sont isométriques. |
|
Après avoir prouvé que des triangles sont isométriques, on peut trouver des mesures manquantes sur l’un ou l’autre des triangles. Voici un exemple où on se sert des conditions minimales pour trouver une mesure manquante.
Il faut d’abord prouver que les triangles sont isométriques avec les informations fournies dans le problème avant de calculer des mesures manquantes.
Trouve la mesure de |\overline{AD}| sachant que |\overline{AC}| est la bissectrice de l’angle |DAB.|

| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les angles |DAC| et |BAC| sont isométriques.||\angle{DAC} \cong \angle{BAC}|| |
A |
|\overline{AC}| est la bissectrice de l’angle |DAB.|||\text{m}\angle{DAC} = \text{m}\angle{BAC}=\dfrac{156^\circ}{2}=78^\circ|| |
|
2 |
Les segments |\overline{CA}| et |\overline{CA}| sont isométriques.||\overline{CA} \cong \overline{CA}|| |
C |
Il s’agit d’un côté commun aux 2 triangles. |
|
3 |
Les angles |ACB| et |ACD| sont isométriques.||\angle{ACB} \cong \angle{ACD}|| |
A |
Puisque la somme des angles intérieurs d’un triangle est de |180^\circ,| on trouve que |\text{m}\angle{ACB}=63^\circ.|||\begin{align}\text{m}\angle{ACB}&=180^\circ-78^\circ-39^\circ\\&=63^\circ\\&=\text{m}\angle{ACD}\end{align}|| |
|
4 |
Les triangles |ADC| et |ABC| sont isométriques.||\triangle ADC \cong \triangle ABC|| |
Ils respectent la condition minimale ACA : des triangles sont isométriques s’ils ont une paire de côtés isométriques compris entre 2 paires d’angles homologues isométriques. |
|
|
5 |
|\text{m}\overline{AD} =6\ \text{cm}| |
Dans les triangles isométriques, les côtés homologues sont isométriques. On a donc l’égalité suivante.||\text{m}\overline{AD}=\text{m}\overline{AB}=6\ \text{cm}|| |
|
Voici un exemple où on se sert des conditions minimales d’isométrie pour compléter une démonstration.
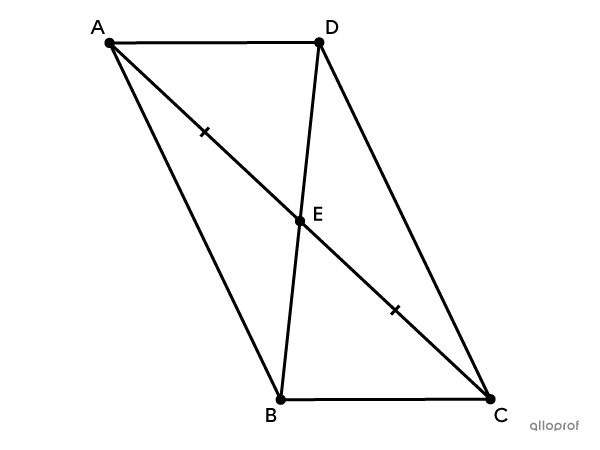
Sur la figure |ABCD| suivante, |\overline{AD}| et |\overline{BC}| sont parallèles et |E| est le point milieu de |\overline{AC}.|
Démontre que le quadrilatère |ABCD| est un parallélogramme.
| Affirmation | Justification | ||
|---|---|---|---|
|
1 |
Les angles |DEA| et |BEC| sont isométriques.||\angle{DEA} \cong \angle{BEC}|| |
A |
Ce sont des angles opposés par le sommet. |
|
2 |
Les segments |\overline{AE}| et |\overline{CE}| sont isométriques.||\overline{AE} \cong \overline{CE}|| |
C |
|E| est le point milieu de |\overline{AC}.| |
|
3 |
Les angles |EAD| et |ECB| sont isométriques.||\angle{EAD} \cong \angle{ECB}|| |
A |
Des angles alternes-internes formés par 2 parallèles |(\overline{AD}| et |\overline{BC})| et une sécante |(\overline{AC})| sont isométriques. |
|
4 |
Les triangles |DEA| et |BEC| sont isométriques.||\triangle DEA \cong \triangle BEC|| |
Ils respectent la condition minimale ACA : des triangles sont isométriques s’ils ont une paire de côtés isométriques compris entre 2 paires d’angles homologues isométriques. |
|
|
5 |
Les segments |\overline{BE}| et |\overline{DE}| sont isométriques.||\overline{BE} \cong \overline{DE}|| |
Puisque ce sont des côtés homologues de triangles isométriques, ils sont isométriques. |
|
|
6 |
|E| est le point milieu de |\overline{BD}.| |
Puisque la mesure de |\overline{BE}| est égale à la mesure de |\overline{DE},| |E| est le point milieu de |\overline{BD}.| |
|
|
7 |
|ABCD| est un parallélogramme. |
Comme |E| est le point milieu de |\overline{AC}| et de |\overline{BC}| et qu’on sait que les diagonales d’un parallélogramme se coupent en leur milieu, on en déduit que |ABCD| est un parallélogramme. |
|
Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante.
