Lorsqu'on compare 2 figures planes, il est possible de vérifier si elles sont isométriques ou semblables en analysant si leurs côtés homologues sont le résultat des mêmes transformations géométriques.
-
Des côtés homologues sont des segments qui ont le même rôle dans des figures différentes.
-
Des angles homologues sont des angles qui ont le même rôle dans des figures différentes.
Lorsqu’on compare 2 figures planes, on pourrait penser que tous les côtés ou les angles homologues sont nécessairement isométriques ou proportionnels. Cependant, comme le montrent les deux paires de triangles suivants, ce n’est pas le cas.
Les côtés |\color{#333fb1}{\overline{BC}}| et |\color{#333fb1}{\overline{JK}}| sont homologues, car ils correspondent au côté le plus long (l’hypoténuse) de leur triangle respectif.
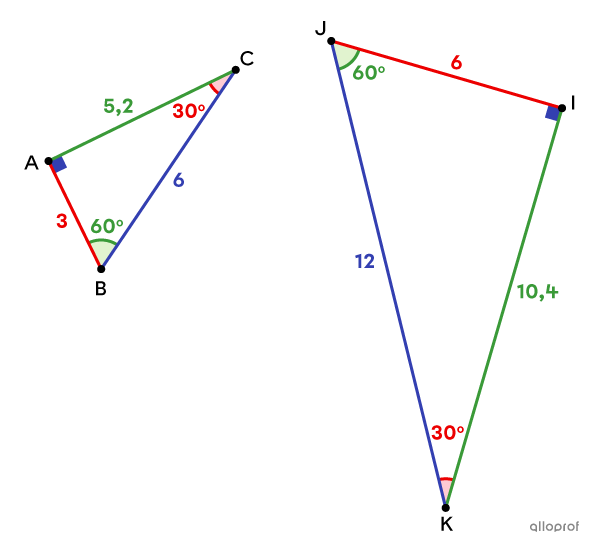
On peut affirmer que |\Delta ABC| et |\Delta IJK| sont semblables, car tous les angles homologues sont isométriques.
Cela implique donc que tous les côtés homologues sont proportionnels.
Les côtés |\color{#333fb1}{\overline{BC}}| et |\color{#333fb1}{\overline{ST}}| sont homologues, car ils correspondent au côté le plus long (l’hypoténuse) de leur triangle respectif.
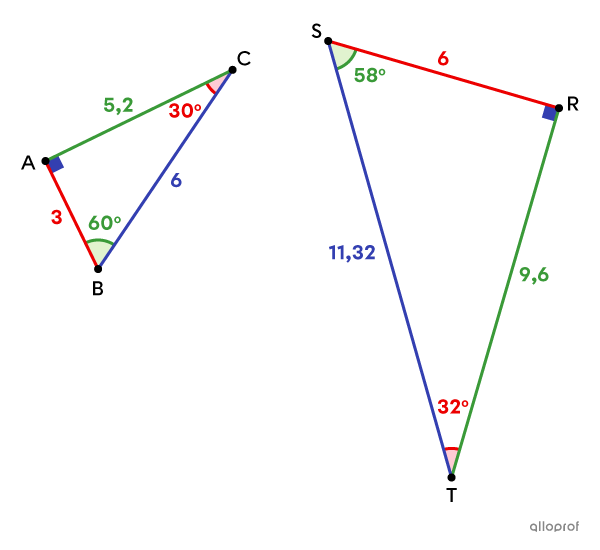
On peut affirmer que |\Delta ABC| et |\Delta RST| ne sont pas semblables, car certains angles homologues ne sont pas isométriques.
Cela implique donc que les côtés homologues ne sont pas proportionnels.
Le mot isométrie prend son origine dans la Grèce antique. Ce mot est formé de iso, qui signifie même, et de métrie, qui signifie mesure.
On dit que 2 figures planes sont isométriques si tous leurs côtés et leurs angles homologues sont isométriques.
Pour savoir si 2 figures sont isométriques, il suffit de démontrer que l’une d’elles (la figure image) est le résultat d’une ou de plusieurs transformations géométriques à partir de l’autre (la figure initiale). Ces transformations géométriques sont les suivantes.
Il est aussi possible de démontrer que 2 figures sont isométriques autrement que par les transformations géométriques. En effet, si tous les côtés homologues sont isométriques, alors il s’agit d’une raison suffisante pour affirmer que ces 2 figures sont isométriques.
Dans l’animation interactive suivante, on peut déplacer les curseurs Translation, Rotation et Réflexion afin de constater l’isométrie entre les 4 pentagones réguliers.
On dit que 2 figures sont congruentes lorsque la figure image est le résultat d’un déplacement, c’est-à-dire d’une translation et/ou d’une rotation seulement. On privilégie donc l’utilisation du mot isométrique, puisqu’on inclut aussi la réflexion, qui n’est pas un déplacement, mais bien un retournement.
Voici un exemple où plusieurs transformations géométriques sont nécessaires pour démontrer que 2 figures sont isométriques.
À l’aide des curseurs Translation et Rotation dans l’animation interactive suivante, trouve la distance de translation et l’angle de rotation qui démontrent que le trapèze orange est isométrique au trapèze rouge.
Par une translation de |12| unités suivie d’une rotation de |100^\circ| par rapport au point |O,| on observe que le trapèze rouge se superpose parfaitement avec le trapèze orange. Ceci implique que tous les côtés homologues et tous les angles homologues sont isométriques. On peut donc conclure que ces 2 trapèzes sont isométriques.
Des figures isométriques sont nécessairement des figures équivalentes.
Cependant, des figures équivalentes ne sont pas nécessairement des figures isométriques.
On dit que 2 figures sont semblables si tous les rapports de côtés homologues sont proportionnels et que tous les angles homologues sont isométriques.
Pour savoir si 2 figures sont semblables, on peut démontrer que l’une d’elles (la figure image) est le résultat d’une homothétie à partir de l’autre (la figure initiale).
Il est aussi possible de démontrer que 2 figures sont semblables autrement que par l’homothétie. En effet, si les quotients des côtés homologues sont tous égaux, alors il s’agit d’une raison suffisante pour affirmer que ces 2 figures sont semblables.
La valeur des quotients des côtés homologues est un rapport noté |k.| Cette valeur correspond au rapport de similitude des 2 figures semblables. Sans tenir compte du signe, le rapport d’homothétie est équivalent au rapport de similitude.
Dans l’animation interactive suivante, on peut déplacer le curseur Rapport d’homothétie afin de voir que les 3 triangles sont semblables par rapport au centre d’homothétie.
Lorsque le rapport d’homothétie vaut |2,| chaque côté du triangle bleu mesure le double de son côté homologue dans le triangle mauve. Lorsque le rapport d’homothétie vaut |0{,}5,| chaque côté du triangle vert mesure la moitié de son côté homologue dans le triangle mauve.
Concernant les angles homologues, on remarque qu’ils sont tous isométriques, peu importe la valeur du rapport d’homothétie.
Il arrive parfois que l’homothétie ne soit pas suffisante pour démontrer la similitude, c’est-à-dire qu’il est aussi nécessaire d’utiliser la translation, la rotation et/ou la réflexion.
Voici un exemple où l’on doit trouver une mesure manquante sachant que 2 figures sont semblables.
Trouve la mesure du côté |\overline{YZ}| sachant que le rectangle |\color{#3a9a38}{ABCD}| est semblable au rectangle |\color{#333fb1}{WXYZ}.|
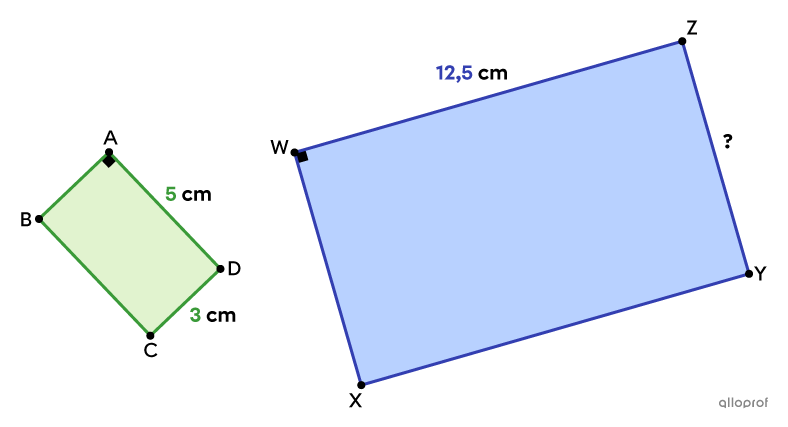
Puisque les 2 rectangles sont semblables, on peut établir une proportion avec les rapports des côtés homologues.
On voit que les côtés |\color{#3a9a38}{\overline{DA}}| et |\color{#333fb1}{\overline{ZW}}| sont homologues, car ils correspondent aux côtés les plus longs de leur rectangle respectif. De même, les côtés |\color{#3a9a38}{\overline{CD}}| et |\color{#333fb1}{\overline{YZ}}| sont homologues, car ils correspondent aux côtés les plus courts de leur rectangle respectif.
On a donc la proportion suivante.
||\begin{align}\dfrac{\color{#3a9a38}{\text{m}\overline{DA}}}{\color{#333fb1}{\text{m}\overline{ZW}}}&=\dfrac{\color{#3a9a38}{\text{m}\overline{CD}}}{\color{#333fb1}{\text{m}\overline{YZ}}}\\\\\dfrac{\color{#3a9a38}{5\ \text{cm}}}{\color{#333fb1}{12{,}5\ \text{cm}}}&=\dfrac{\color{#3a9a38}{3\ \text{cm}}}{\color{#333fb1}{\text{m}\overline{YZ}}}\end{align}||
On peut ensuite utiliser le produit croisé pour éliminer les fractions.
||\begin{align}\dfrac{5\ \text{cm}}{12{,}5\ \text{cm}}&=\dfrac{3\ \text{cm}}{\text{m}\overline{YZ}}\\\\\text{m}\overline{YZ}\times5\ \text{cm}&=3\ \text{cm}\times12{,}5\ \text{cm}\end{align}||
Finalement, on isole |\text{m}\overline{YZ}| à l’aide de la méthode de la balance.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{\text{m}\overline{YZ}\times\color{#ec0000}{\cancel{\color{black}{5\ \text{cm}}}}}}{\cancel{5\ \text{cm}}}}&=\color{#ec0000}{\dfrac{\color{black}{3\ \text{cm}\times12{,}5\ \text{cm}}}{5\ \text{cm}}}\\\\\text{m}\overline{YZ}&=7{,}5\ \text{cm}\end{align}||
Réponse : La mesure du côté |\overline{YZ}| est |7{,}5\ \text{cm}.|