La parabole fait partie des coniques. Elle s’obtient par l’intersection d’une surface conique et d’un plan.
Une parabole est le lieu géométrique de tous les points situés à égale distance d’une droite fixe, appelée directrice, et d'un point fixe, appelé foyer.
-
La parabole possède un foyer, |F.|
-
La parabole possède un sommet, |S.|
-
La parabole possède une droite, appelée directrice.
-
La droite perpendiculaire à la directrice de la parabole et qui passe par le foyer et le sommet est l'axe de symétrie.
-
Le sommet |S| est équidistant au foyer |F| et à la directrice.
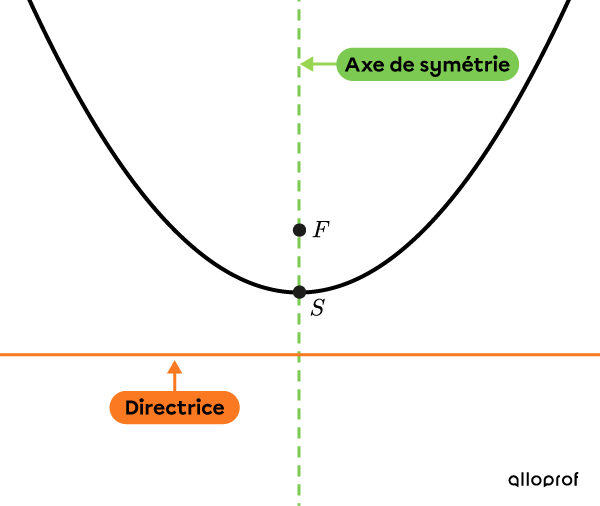
Parabole verticale
Lorsque l’axe de symétrie est vertical, la parabole est verticale.
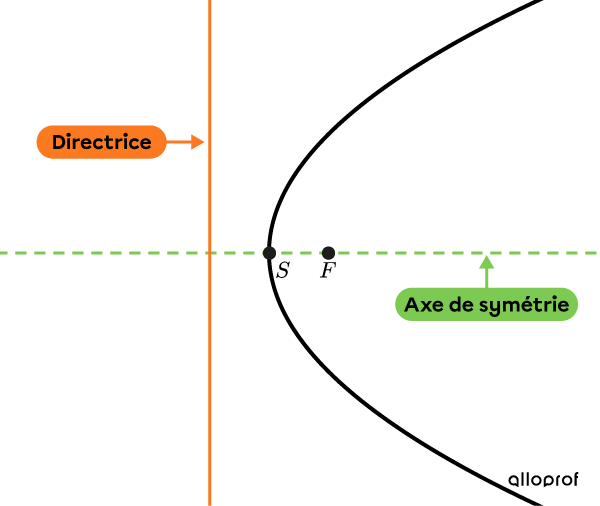
Parabole horizontale
Lorsque l’axe de symétrie est horizontal, la parabole est horizontale.
L'équation qui définit la parabole centrée à l’origine utilise le paramètre |c.| On distingue 2 équations différentes selon son orientation.
Parabole verticale
||x^2=4cy||Équation de la directrice : ||y=-c||
Parabole horizontale
||y^2=4cx||Équation de la directrice : ||x=-c||
où
|\vert c \vert :| distance entre le sommet et le foyer ou entre le sommet et la directrice
Dans l’équation de la parabole verticale, |x| est au carré, tandis que dans la parabole horizontale, c’est |y| qui est au carré.
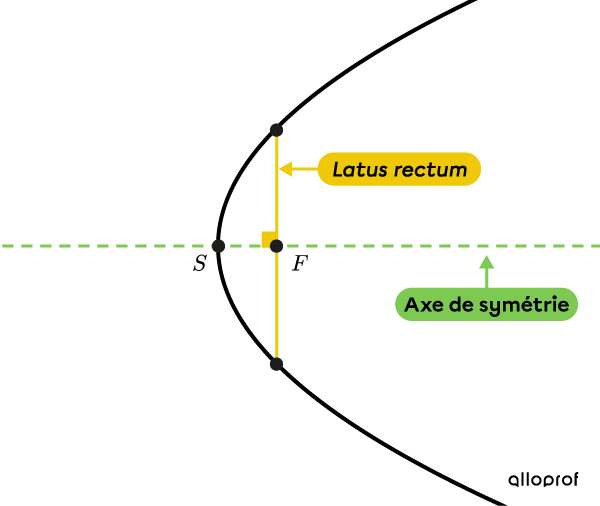
Le latus rectum est un segment de droite qui passe par le foyer de la parabole et qui est perpendiculaire à son axe de symétrie. La longueur du latus rectum de la parabole est |4c.| Le latus rectum détermine l’ouverture de la parabole au foyer.
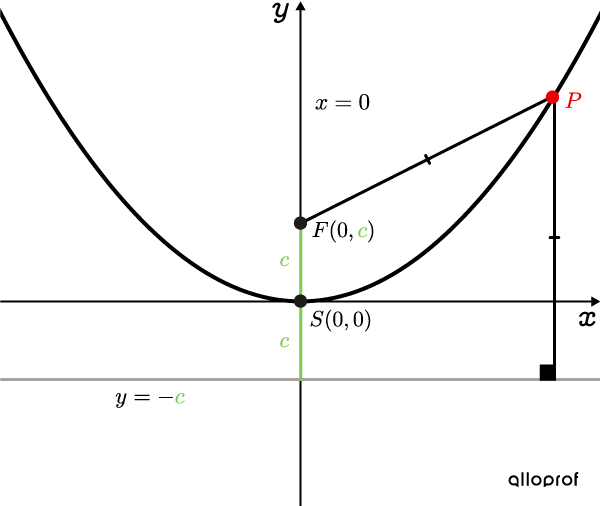
Voici les représentations graphiques des 2 types de paraboles sur lesquelles sont placés les points importants et leurs coordonnées.
Parabole verticale
Si |c>0,| la parabole est ouverte vers le haut.
Si |c<0,| la parabole est ouverte vers le bas.
Parabole horizontale
Si |c>0,| la parabole est ouverte vers la droite.
Si |c<0,| la parabole est ouverte vers la gauche.
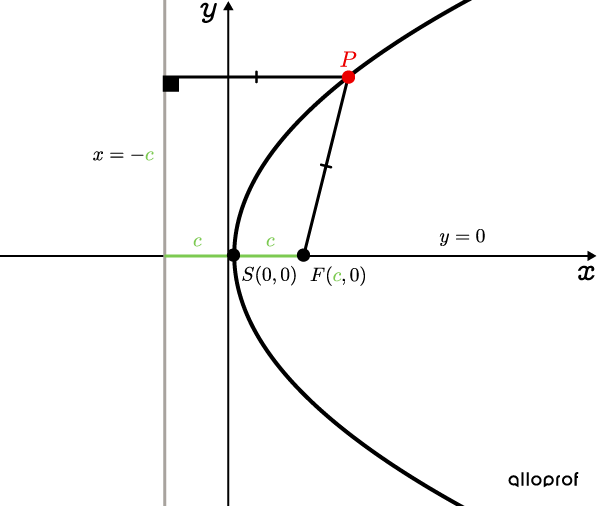
Tous les points |\color{#EC0000}P| sont situés à égale distance de la directrice et du foyer |F.|
Pour déterminer l’équation d’une parabole centrée à l’origine, il faut trouver la valeur du paramètre |c.|
-
Déterminer le signe du paramètre |\color{#3a9a38}c| ainsi que l'équation à utiliser à l'aide de l'orientation de la parabole.
-
Déterminer la valeur du paramètre |\color{#3a9a38}c| à l’aide de l’une des stratégies suivantes.
a) Si l’équation de la directrice est fournie, déduire la valeur de |\color{#3a9a38}c.|
b) Si les coordonnées du foyer sont fournies, déduire la valeur de |\color{#3a9a38}c.|
c) Si un point de la parabole est fourni, substituer toutes les informations dans l’équation de la parabole.
-
Écrire l'équation de la parabole.
Voici un exemple où l’équation de la directrice est fournie.
Détermine l'équation de la parabole suivante.

-
Déterminer le signe du paramètre |c| ainsi que l'équation à utiliser
La parabole est horizontale et ouverte vers la droite. Le paramètre |c| sera donc positif et l'équation sera de la forme suivante. ||y^2=4cx|| -
Déterminer la valeur du paramètre |c|
Comme l’équation de la directrice est |x=-10,| cela signifie que |\color{#3a9a38}{c}=\color{#3a9a38}{10}.| -
Écrire l'équation de la parabole
En remplaçant la valeur des paramètres, on obtient : ||\begin{align}y^2&=4\color{#3a9a38}cx\\y^2&=4(\color{#3a9a38}{10})x\\ y^2&=40x\end{align}||
-
Déterminer l'orientation de la parabole.
-
Déterminer les coordonnées du foyer et l’équation de la droite directrice à l'aide du paramètre |\color{#3a9a38}{c}.|
-
Trouver d'autres points sur la parabole à l'aide de l'équation.
-
Tracer la parabole et sa droite directrice.
Trace la parabole dont l’équation est |x^2=14y.|
-
Déterminer l’orientation de la parabole
Comme c’est |x| qui est au carré, la parabole est verticale. De plus, le paramètre |c| est positif. La parabole sera donc ouverte vers le haut. -
Déterminer les coordonnées du foyer et l’équation de la droite directrice ||\begin{align}
4c&=14\\c&=\dfrac{14}{4}\\\color{#3a9a38}{c}&=\color{#3a9a38}{3{,}5}\end{align}|| Le foyer est le point |(0\ ;3{,}5)| et l’équation de la droite directrice est : ||\begin{align}y&=-\color{#3a9a38}{c}\\y&=-\color{#3a9a38}{3{,}5}\end{align}|| -
Trouver d'autres points sur la parabole à l'aide de l'équation
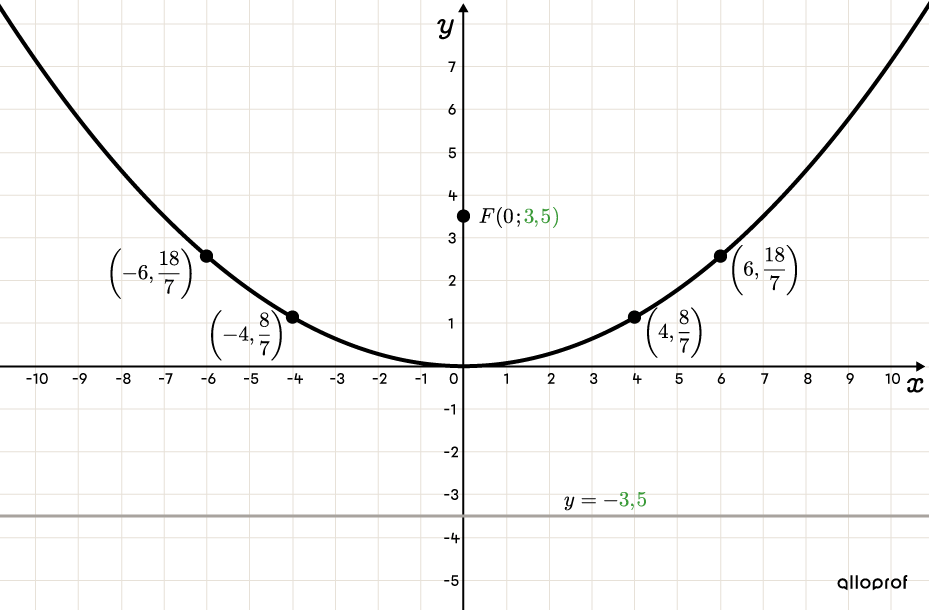
Si |x=4,| on a : ||\begin{align}x^2&=14y\\(4)^2&=14y\\16&=14y\\\dfrac{8}{7}&=y\end{align}||La parabole passe par le point |\left(4,\dfrac{8}{7}\right).| Comme la parabole est symétrique par rapport à l’axe |x=0,| on déduit qu’elle passe aussi au point |\left(-4,\dfrac{8}{7}\right).|
En suivant le même principe, on trouve les points |\left(6,\dfrac{18}{7}\right)| et |\left(-6,\dfrac{18}{7}\right).| -
Tracer la parabole et sa droite directrice
Voici une animation permettant de bien saisir les différentes relations et le rôle des paramètres dans la parabole.
L'équation qui définit la parabole non centrée utilise les paramètres |c,| |h| et |k.| Comme avec la parabole centrée, on distingue 2 équations différentes selon son orientation.
Parabole verticale
||(x-h)^2=4c(y-k)|| Équation de la directrice : ||y=k-c||
Parabole horizontale
||(y-k)^2=4c(x-h)|| Équation de la directrice : ||x=h-c||
où
|\vert c \vert :| distance entre le sommet et le foyer ou entre le sommet et la directrice
|(h,k) :| coordonnées du sommet de la parabole
Voici les représentations graphiques des 2 types de paraboles sur lesquelles sont placés les points importants et leurs coordonnées.
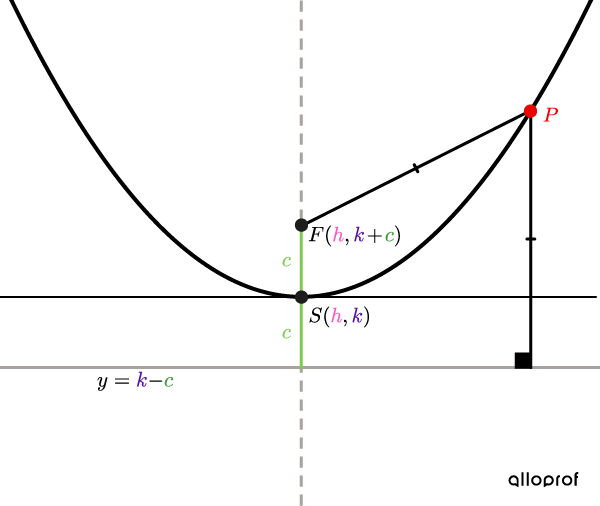
Parabole verticale
Si |c>0,| la parabole est ouverte vers le haut.
Si |c<0,| la parabole est ouverte vers le bas.
Parabole horizontale
Si |c>0,| la parabole est ouverte vers la droite.
Si |c<0,| la parabole est ouverte vers la gauche.
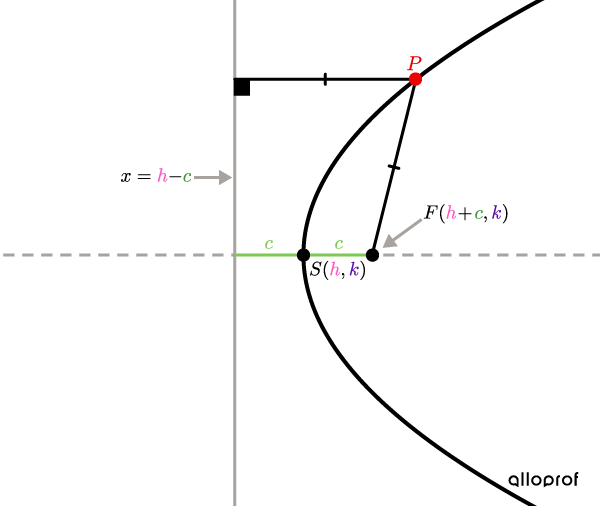
Tous les points |\color{#EC0000}P| sont situés à égale distance de la directrice et du foyer |F.|
Pour déterminer l’équation d’une parabole non centrée à l’origine, il faut trouver la valeur des paramètres |c,| |h| et |k.|
-
Déterminer le signe du paramètre |\color{#3a9a38}c| ainsi que l'équation à utiliser à l'aide de l'orientation de la parabole.
-
Déterminer la valeur des paramètres |\color{#3a9a38}c,| |\color{#FF55C3}h| et |\color{#560FA5}k.| Si l’un ou plusieurs de ces paramètres sont manquants, utiliser l’une des stratégies suivantes :
a) Si le sommet et l’équation de la directrice sont fournis, déterminer le paramètre |\color{#3a9a38}c| en substituant les informations dans l’équation de la directrice.
b) Si le sommet et un point appartenant à la parabole sont fournis, déterminer le paramètre |\color{#3a9a38}c| en substituant les informations dans l’équation de la parabole.
c) Si les coordonnées du foyer et l’équation de la directrice sont fournies, déduire les paramètres manquants à l’aide des propriétés de la parabole.
-
Écrire l'équation de la parabole.
Voici un exemple où l’équation de la directrice est fournie de même que les coordonnées du foyer.
Détermine l'équation de la parabole suivante.
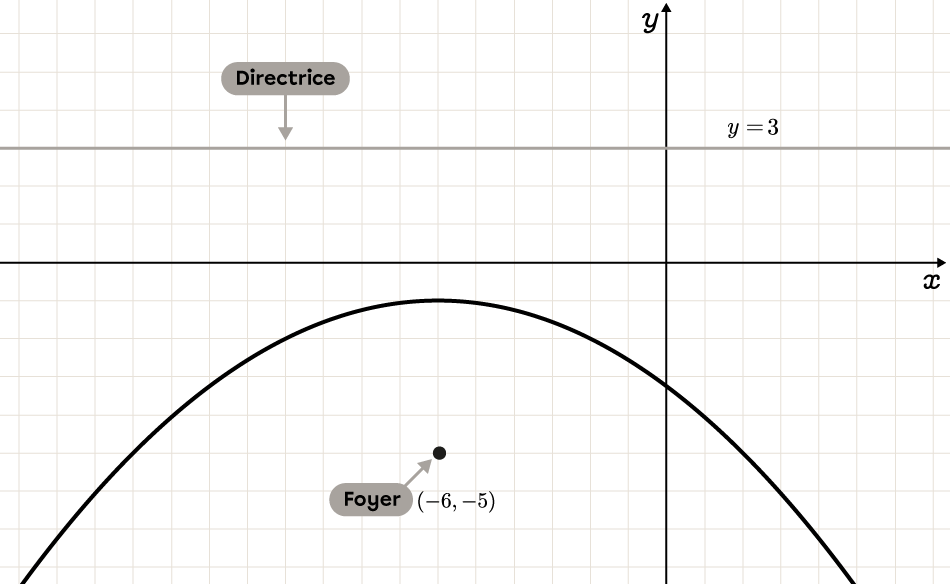
-
Déterminer le signe du paramètre |c| ainsi que l'équation à utiliser
Comme la parabole est verticale et ouverte vers le bas, |\color{#3a9a38}c| est négatif et l’équation à utiliser est la suivante. ||(x-h)^2=4c(y-k)|| -
Déterminer les paramètres manquants
Dans ce cas-ci, il manque les 3 paramètres pour déterminer l’équation de la parabole. On doit alors utiliser ses propriétés à l’aide des informations fournies.
On sait que la distance entre le foyer et le sommet est égale à la distance entre la directrice et le sommet. La distance verticale entre le foyer et la directrice est donc |2\vert\color{#3a9a38}c\vert.| ||\begin{align}2\vert\color{#3a9a38}c\vert &=\vert3--5\vert \\2\vert\color{#3a9a38}c\vert &=\vert8\vert\\ \vert\color{#3a9a38}c\vert&=\color{#3a9a38}4\end{align}||Comme on sait que |c| est négatif, on a : ||\color{#3a9a38}c=\color{#3a9a38}{-4}||On peut trouver les coordonnées |(\color{#FF55C3}h,\color{#560FA5}k)| du sommet en additionnant la valeur de |\vert \color{#3a9a38}c\vert| à l'ordonnée du foyer. ||\begin{align}
(\color{#FF55C3}h,\color{#560FA5}k)&=(\color{#FF55C3}{-6},-5+\color{#3a9a38}{4})\\
&= (\color{#FF55C3}{-6},\color{#560FA5}{-1})
\end{align}||
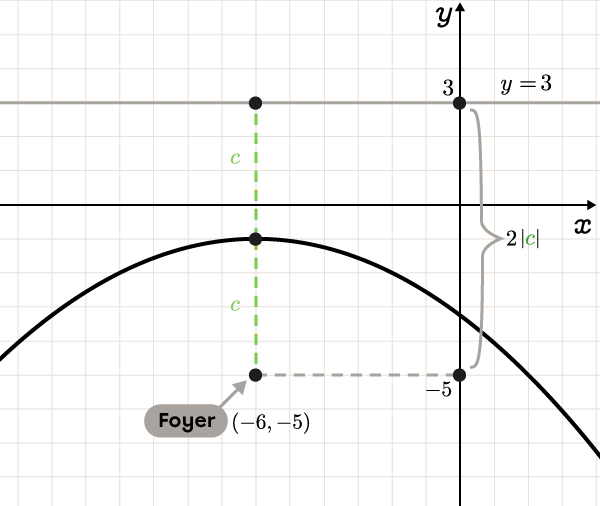
-
Écrire l'équation de la parabole
En remplaçant la valeur des paramètres, on obtient : ||\begin{align}(x-\color{#FF55C3}h)^2&=4\color{#3a9a38}c(y-\color{#560FA5}k)\\(x-\color{#FF55C3}{-6})&=4(\color{#3a9a38}{-4})(y-\color{#560FA5}{-1})\\(x+6)^2&=-16(y+1)\end{align}||
-
Identifier les paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| dans l'équation et placer le sommet de la parabole.
-
Déterminer l’orientation de la parabole.
-
Déterminer les coordonnées du foyer et l’équation de la droite directrice à l'aide du paramètre |\color{#3a9a38}c.|
-
Trouver d'autres points sur la parabole à l'aide de l'équation.
-
Tracer la parabole et sa droite directrice.
Trace la parabole dont l'équation est |(y-1)^2=-8(x+3).|
-
Identifier les paramètres |h| et |k| dans l'équation et placer le sommet de la parabole
Selon l’équation, on détermine que le sommet se situe aux coordonnées suivantes. ||(\color{#FF55C3}h,\color{#560fa5}k)=(\color{#FF55C3}{-3},\color{#560fa5}{1})|| -
Déterminer l’orientation de la parabole
Comme c’est la parenthèse qui contient le terme |y| qui est au carré, la parabole est horizontale. De plus, le paramètre |c| est négatif. La parabole sera donc ouverte vers la gauche. -
Déterminer les coordonnées du foyer et l’équation de la droite directrice ||\begin{align}4\color{#3a9a38}c&=-8\\\color{#3a9a38}c&=\dfrac{-8}{4}\\\color{#3a9a38}{c}&=\color{#3a9a38}{-2}\end{align}||Le foyer est aux coordonnées suivantes. ||\begin{align}(\color{#FF55C3}h+\color{#3a9a38}{c}&,\color{#560fa5}k)\\(\color{#FF55C3}{-3}+\color{#3a9a38}{-2}&,\color{#560fa5}{1})\\(-5&,1)\end{align}||L’équation de la droite directrice est la suivante. ||\begin{align}x&=\color{#FF55C3}h-\color{#3a9a38}{c}\\x&=\color{#FF55C3}{-3}-\color{#3a9a38}{-2}\\x&=-1\end{align}||
-
Trouver d'autres points sur la parabole à l'aide de l'équation
Comme c’est |y| qui est au carré, on peut choisir une valeur à |y| pour déterminer le |x| correspondant. Si |y=5,| on a : ||\begin{align}(y-1)^2&=-8(x+3)\\(5-1)^2&=-8(x+3)\\16&=-8(x+3)\\-2&=x+3\\-5&=x\end{align}||La parabole passe par le point |(-5,5).| Puisqu’elle est horizontale et que son foyer est à |(-5,1)|, l’ordonnée est à une distance verticale de |4| unités par rapport au foyer. On peut donc déduire l’ordonnée de son point symétrique, qui sera aussi à une distance de |4| unités. On trouve le point |(-5,-3).| -
Tracer la parabole et sa droite directrice

Lorsqu’on veut représenter une région délimitée par une parabole, on applique les relations suivantes.
L'intérieur d'une parabole correspond à la région où se situe le foyer. Les signes d’inéquation sont alors plus petit |(<)| ou plus petit ou égal |(\leq).|
À l’inverse, l’extérieur est la région où n’est pas situé le foyer. Les signes sont alors plus grand |(>)| ou plus grand ou égal |(\geq).|
Parabole verticale |
||
| Secteur du plan | Représentation graphique | Inéquation correspondante |
|---|---|---|
|
L’intérieur, excluant la courbe |
 |
||\begin{align}x^2&<4cy\\\\ |
|
L’extérieur, excluant la courbe |
 |
||\begin{align}x^2&>4cy\\\\ |
Parabole horizontale |
||
| Secteur du plan | Représentation graphique | Inéquation correspondante |
|
L’intérieur, excluant la courbe |
 |
||\begin{align}y^2&<4cx\\\\ |
|
L’extérieur, excluant la courbe |
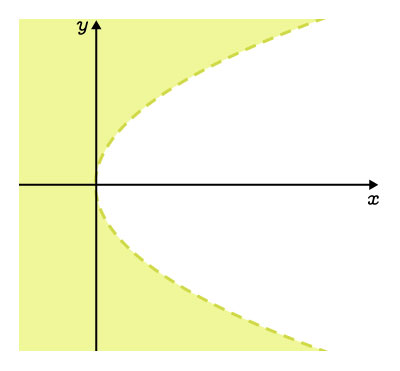 |
||\begin{align}y^2&>4cx\\\\ |
Si on veut inclure les points qui sont sur la parabole, on change respectivement les symboles d'inéquations |<,>| pour les symboles |\leq,\geq.|