Le cercle fait partie des coniques. Il s’obtient par l’intersection d’une surface conique et d’un plan.
Le cercle est le lieu géométrique de tous les points situés à égale distance d’un point nommé centre.
Tout point |(x,y)| qui appartient au cercle peut être trouvé grâce au théorème de Pythagore (aussi appelé relation de Pythagore).
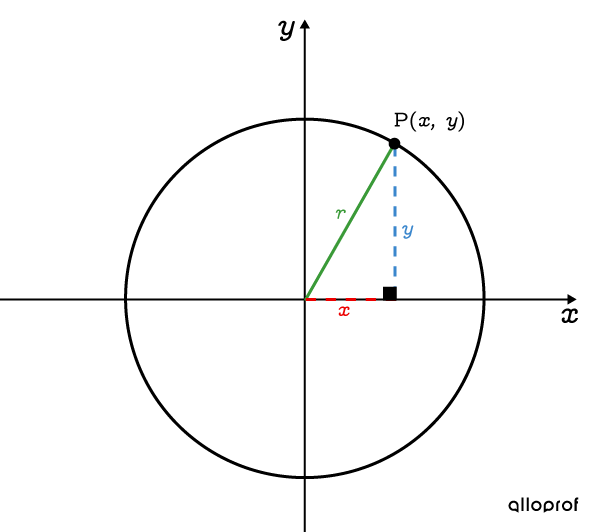
L'équation qui définit le cercle centré à l’origine utilise le paramètre |r.|
||x^2+ y^2= r^2||
où
||r=\text{rayon du cercle}||
Pour déterminer l’équation d’un cercle centré à l’origine, il faut trouver la valeur du rayon |r.|
-
Déterminer la valeur du paramètre |\color{#3a9a38}r,| le rayon du cercle. Au besoin, substituer |x| et |y| par un point du cercle et résoudre l'équation.
-
Écrire l'équation du cercle.
Détermine l’équation du cercle centré à l’origine qui passe par le point |(7,-3).|
-
Déterminer la valeur du paramètre |r|
On remplace |x| et |y| dans l’équation du cercle centré. ||\begin{align}x^2+ y^2&= \color{#3a9a38}r^2\\7^2+ (-3)^2&=\color{#3a9a38}r^2\\49+9&=\color{#3a9a38}r^2\\ 58&=\color{#3a9a38}r^2\\ \sqrt{58}&=\color{#3a9a38}r\end{align}|| -
Écrire l’équation du cercle
En remplaçant la valeur du paramètre |r| par |\sqrt{58}| dans l’équation de base, on obtient l’équation recherchée : ||\begin{align}x^2+y^2&=\color{#3a9a38}r^2\\ x^2+y^2&=(\color{#3a9a38}{\sqrt{58}})^2\\ x^2+y^2&=58\end{align}||
-
Placer le centre du cercle à l’origine du plan cartésien.
-
Déterminer le paramètre |\color{#3a9a38}r| à l’aide de l'équation.
-
Avec un compas, tracer à partir du centre un cercle dont le rayon est égal à |\color{#3a9a38}r.|
Trace le cercle d’équation |x^2+y^2=36.|
-
Placer le centre du cercle
Comme le cercle est centré à l’origine, le centre se trouve au point |(0,0).| -
Déterminer le paramètre |r|
||\color{#3a9a38}r=\sqrt{36}=\color{#3a9a38}6|| -
Tracer le cercle avec un compas
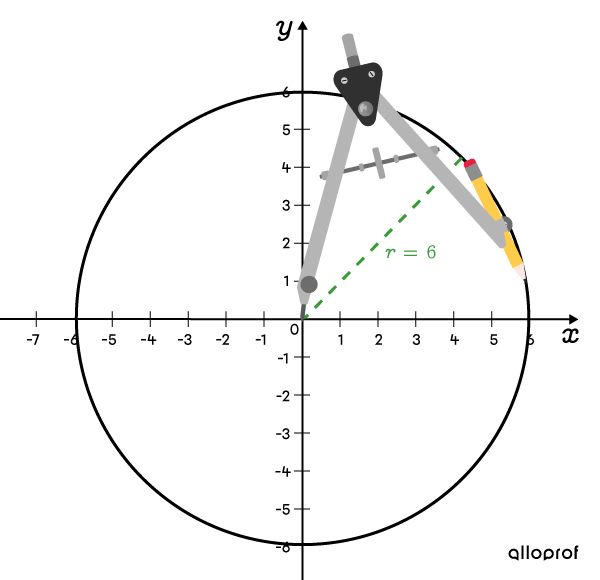
Même si le cercle n'est pas centré à l'origine, on peut tout de même utiliser le théorème de Pythagore pour tout point |(x,y)| qui appartient au cercle.
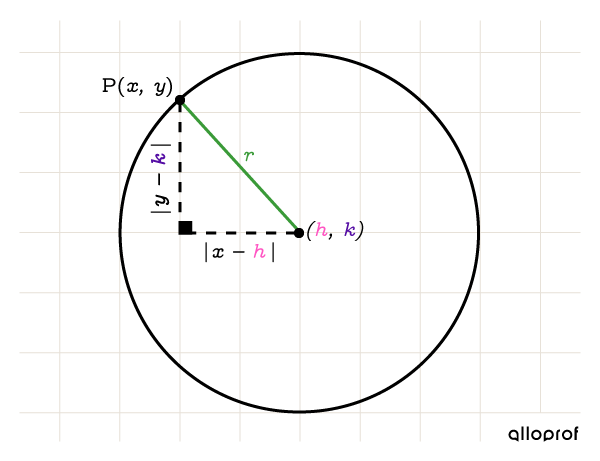
L'équation qui définit le cercle non centré à l’origine utilise les paramètres |r,| |h| et |k.|
||(x-h)^2+(y-k)^2= r^2||
où
||\begin{align} r&=\text{rayon du cercle}\\ (h,k)&=\text{coordonnées du centre du cercle}\end{align}||
Pour déterminer l’équation d’un cercle non centré à l’origine, il faut trouver la valeur du rayon |r| et des coordonnées |(h, k)| du centre.
-
Déterminer la valeur des paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| à partir des coordonnées du centre du cercle.
-
Déterminer la valeur du paramètre |\color{#3a9a38}r,| le rayon du cercle. Au besoin, substituer |x| et |y| par un point du cercle et résoudre l'équation.
-
Écrire l’équation du cercle.
Détermine l'équation d'un cercle qui passe par les points |(-1, 0)| et |(-1, 4).|
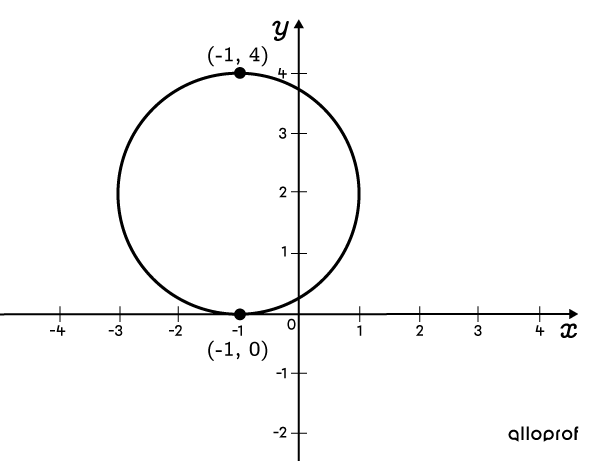
-
Déterminer la valeur des paramètres |h| et |k|
On remarque que les 2 points donnés sont à l’opposé l’un de l’autre puisqu’ils ont la même abscisse, mais pas la même ordonnée. Ainsi, le segment qui les relie est un diamètre et le point milieu de ce segment est le centre du cercle. Le centre a la même abscisse que les 2 points : |\color{#ff55c3}h=\color{#ff55c3}{-1}.| Il reste à déterminer son ordonnée. ||\color{#560fa5}k=\dfrac{4+0}{2} =\color{#560fa5}{2}|| -
Déterminer la valeur du paramètre |r|
Puisque le diamètre du cercle mesure |4,| le rayon du cercle est ||\color{#3a9a38}r=\dfrac{4}{2}=\color{#3a9a38}2|| -
Écrire l’équation du cercle
On obtient : ||\begin{align}(x-\color{#ff55c3}h)^2+(y-\color{#560fa5}k)^2&= \color{#3a9a38}r^2\\ \big(x-(\color{#ff55c3}{-1})\big)^2+(y-\color{#560fa5}2)^2&=\color{#3a9a38}{2}^2\\ (x+1)^2+(y-2)^2&=4\end{align}||
-
Identifier les paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| dans l'équation et placer le centre du cercle.
-
Déterminer le paramètre |\color{#3a9a38}r| dans l'équation.
-
Avec un compas, tracer à partir du centre un cercle dont le rayon est égal à |\color{#3a9a38}r.|
Trace le cercle d’équation |(x+4)^2+(y-3)^2=16.|
-
Identifier les paramètres |h| et |k| dans l’équation et placer le centre
Selon l’équation, on détermine que le centre se situe aux coordonnées suivantes : ||(\color{#FF55C3}h,\color{#560FA5}k)=(\color{#FF55C3}{-4},\color{#560FA5}{3})||
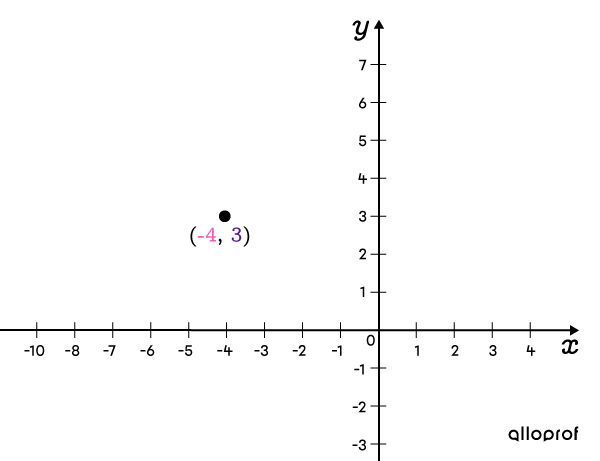
-
Déterminer le paramètre |r|
||\color{#3a9a38}r=\sqrt{16}=\color{#3a9a38}4|| -
Tracer le cercle avec un compas
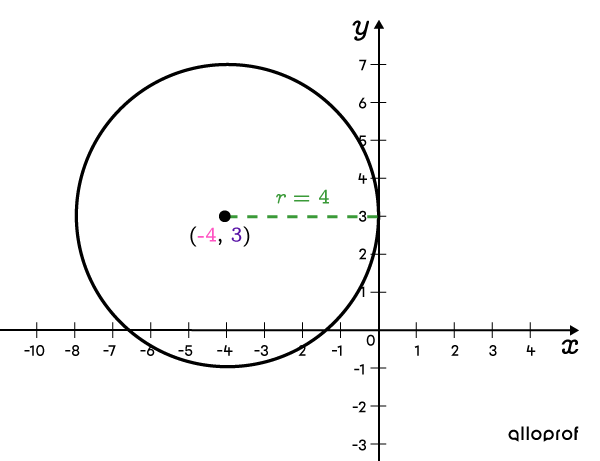
Lorsqu'on veut représenter une région délimitée par un cercle, on applique les relations suivantes.
| Secteur du plan | Représentation graphique | Inéquation correspondante |
|---|---|---|
|
L'extérieur, excluant la courbe |
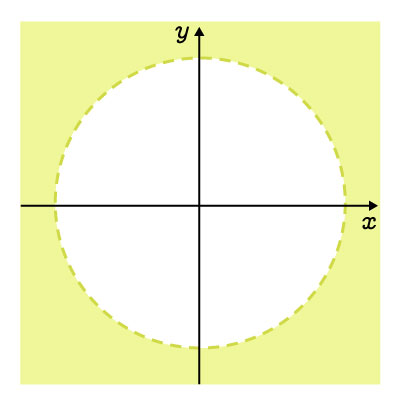 |
||\begin{align}x^2&+y^2>r^2\\\\(x-h)^2&+(y-k)^2>r^2\end{align}|| |
|
L'intérieur, excluant la courbe |
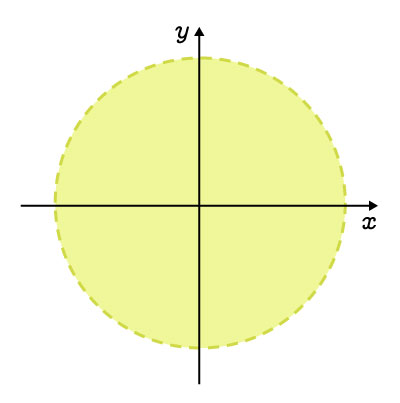 |
||\begin{align}x^2&+y^2<r^2\\\\(x-h)^2&+(y-k)^2<r^2\end{align}|| |
|
L'extérieur du cercle, incluant la courbe |
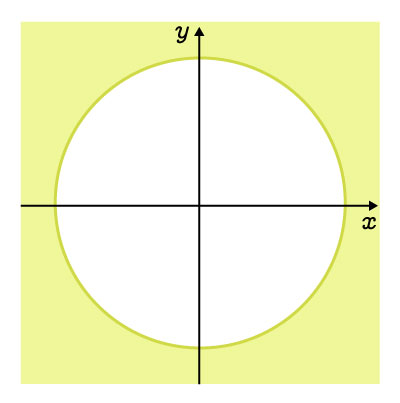 |
||\begin{align}x^2&+y^2\geq r^2\\\\(x-h)^2&+(y-k)^2\geq r^2\end{align}|| |
|
L'intérieur du cercle, incluant la courbe |
 |
||\begin{align}x^2&+y^2\leq r^2\\\\(x-h)^2&+(y-k)^2\leq r^2\end{align}|| |
Une tangente à un cercle est une droite perpendiculaire au rayon qui passe au point de tangence.
-
Déterminer la pente de la droite passant par le centre du cercle et le point de tangence.
-
Déterminer la pente de la tangente grâce à la relation entre 2 droites perpendiculaires.
-
Déterminer l’ordonnée à l’origine de la tangente à l’aide de sa pente et des coordonnées du point de tangence.
-
Écrire l’équation de la droite tangente.
Détermine l'équation de la tangente au cercle d'équation |(x+1)^2+(y-2)^2=25| au point |(2,6).|
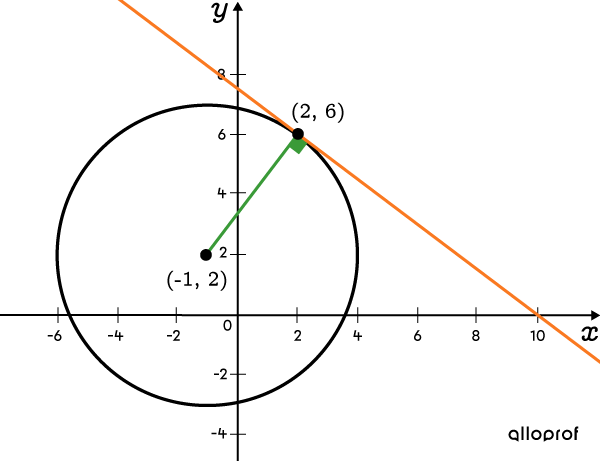
-
Déterminer la pente de la droite passant par le centre du cercle et le point donné
Le centre du cercle est situé aux coordonnées |(-1,2).| On calcule la pente de la droite passant par le centre du cercle et le point de tangence |(2,6).| ||\begin{align}a&=\frac{y_2-y_1}{x_2-x_1}\\ \\&= \frac{6-2}{2--1}\\ \\&=\frac{4}{3}\end{align}|| -
Déterminer la pente de la tangente
La pente de la tangente est toujours l'opposée de l'inverse de la pente de la droite qui supporte le rayon. Ainsi, la pente de la tangente est |a = - \dfrac{3}{4}.| -
Déterminer l'ordonnée à l'origine de la tangente
Pour déterminer l'ordonnée à l'origine, on remplace |a| par la pente de la tangente et |x| et |y| par les coordonnées du point de tangence. On obtient : ||\begin{align}y&=ax+b \\ 6&={-\dfrac{3}{4}}(2)+b\\6&=-\dfrac{3}{2}+b\\ \dfrac{15}{2}&=b\end{align}|| -
Écrire l'équation de la droite tangente
Ainsi, l'équation de la tangente est la suivante. ||y =-\dfrac{3}{4}x +\dfrac{15}{2}||
L'équation générale de toutes les coniques, dont le cercle, pour lesquelles l'axe horizontal est parallèle à l'axe des abscisses et l'axe vertical est parallèle à l'axe des ordonnées est || Ax^2+ By^2+Cx+Dy+E=0.||
Pour retrouver cette forme, il faut développer l'équation canonique d'un cercle : ||\begin{align}(x-h)^2 + (y-k)^2 &= r^2\\ (x-h)(x-h) + (y-k)(y-k) &= r^2 \\ x^2 - 2hx + h^2 + y^2 - 2ky + k^2 &= r^2 \\x^2 + y^2 - 2hx - 2ky + h^2 + k^2 &= r^2 \\ x^2 + y^2 \color{#ec0000}{- 2h}x \color{#3b87cd}{- 2k}y +\color{#3a9a38}{(h^2 + k^2 - r^2)} &=0 \\ x^2 + y^2 + \color{#ec0000}{C}x + \color{#3b87cd}{D}y + \color{#3a9a38}{E} &= 0\end{align}||
où ||\begin{align}A&=1\\B&=\ 1\\\color{#ec0000}{C}&=\color{#ec0000}{-2h}\\ \color{#3b87cd}D&=\color{#3b87cd}{-2k}\\ \color{#3a9a38}E&=\color{#3a9a38}{h^2 + k^2 - r^2}\end{align}||