L’hyperbole fait partie des coniques. Elle s’obtient par l’intersection d’une surface conique et d’un plan perpendiculaire à la base de la conique.
Une hyperbole est le lieu géométrique de tous les points dont la différence des distances à 2 points fixes, appelés foyers, est constante.
-
L'hyperbole possède 2 sommets, |S_1| et |S_2.|
-
L'hyperbole possède 2 foyers, |F_1| et |F_2.|
-
L'hyperbole possède 2 asymptotes.
-
La droite passant par les 2 foyers et les 2 sommets est l'axe transversal.
-
La droite qui passe par le point d'intersection entre les asymptotes et qui est perpendiculaire à l'axe transversal est l'axe conjugué.
-
On peut former un rectangle passant par les sommets de l'hyperbole et étant délimité par l’intersection avec les asymptotes.
-
L’hyperbole peut être verticale ou horizontale.
Hyperbole verticale
Lorsque l’axe transversal est vertical, l’hyperbole est verticale.
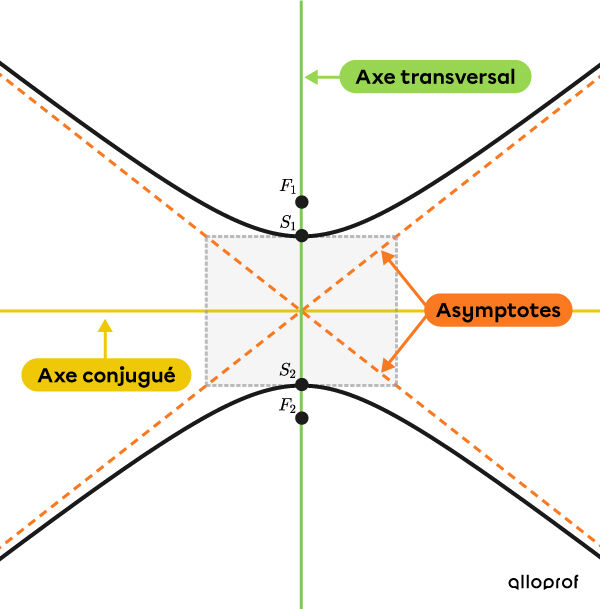
Hyperbole horizontale
Lorsque l’axe transversal est horizontal, l’hyperbole est horizontale.
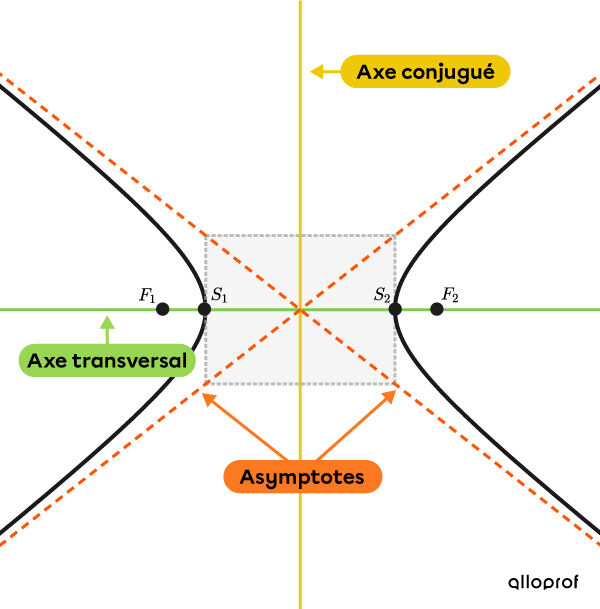
L'équation qui définit l’hyperbole centrée à l’origine utilise les paramètres |a| et |b.| On distingue 2 équations différentes selon son orientation. Il arrive aussi qu’on doive déterminer l’équation des droites constituant les asymptotes de la courbe.
Hyperbole verticale
||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1|| où ||\begin{align} a&:\text{la moitié de la largeur du rectangle}\\ b&:\text{la distance entre un sommet et son centre} \end{align}||
Hyperbole horizontale
||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1|| où ||\begin{align} a&:\text{la distance entre un sommet et son centre}\\ b&:\text{la moitié de la hauteur du rectangle}\end{align}||
Équation des asymptotes
||\begin{align}\text{Asymptote croissante :}\ \ y&=\dfrac{b}{a}x\\\\ \text{Asymptote décroissante :}\ \ y&=-\dfrac{b}{a}x\end{align}||
On place le terme |x| en premier et le terme |y| en deuxième, séparés par une soustraction. L’équation de l’hyperbole verticale est égale à |-1,| tandis que l’hyperbole horizontale est égale à |1.|
Voici les représentations graphiques des 2 types d’hyperboles centrées à l’origine sur lesquelles sont placés les sommets, les foyers et les asymptotes.
Hyperbole verticale
Les points dont la différence des distances à 2 points fixes (foyers) est de |2\color{#3b87cd}b.|
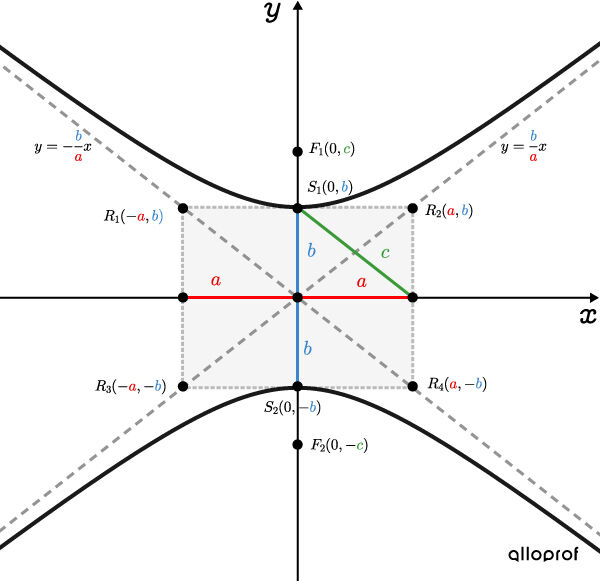
Hyperbole horizontale
Les points dont la différence des distances à 2 points fixes (foyers) est de |2\color{#ec0000}a.|
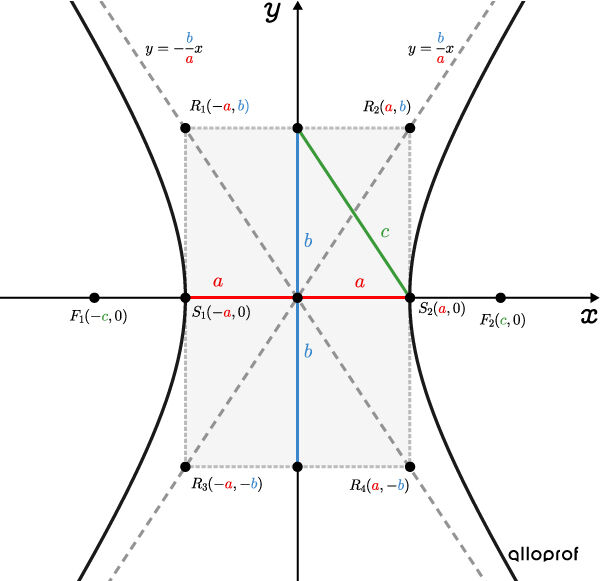
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
Afin de déterminer l'équation d'une hyperbole centrée à l’origine, il faut trouver la valeur des paramètres |a| et |b.|
Généralement, on utilise la démarche suivante.
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole.
-
À l’aide des informations fournies par rapport aux sommets, déterminer la valeur du paramètre |\color{#ec0000}a| et/ou du paramètre |\color{#3B87CD}b.|
-
Déterminer le paramètre manquant, s’il y a lieu. Pour ce faire, utiliser une des stratégies suivantes :
a) Si le paramètre |\color{#3A9A38}c| (la distance entre le centre et un foyer) est fourni, utiliser le théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
b) Si un couple |(x,y)| appartenant à l’hyperbole est fourni, substituer toutes les informations dans l'équation de l’hyperbole.
c) Si un couple |(x,y)| appartenant à l’une des asymptotes est fourni, substituer toutes les informations dans l'équation de l’asymptote.
d) Si l’équation de l’une des asymptotes est fournie, utiliser le taux de variation |\dfrac{\color{#3b87cd}b}{\color{#ec0000}a}.|
-
Écrire l’équation de l’hyperbole.
Voici un exemple où le sommet et le foyer sont fournis.
Détermine l’équation de cette hyperbole.
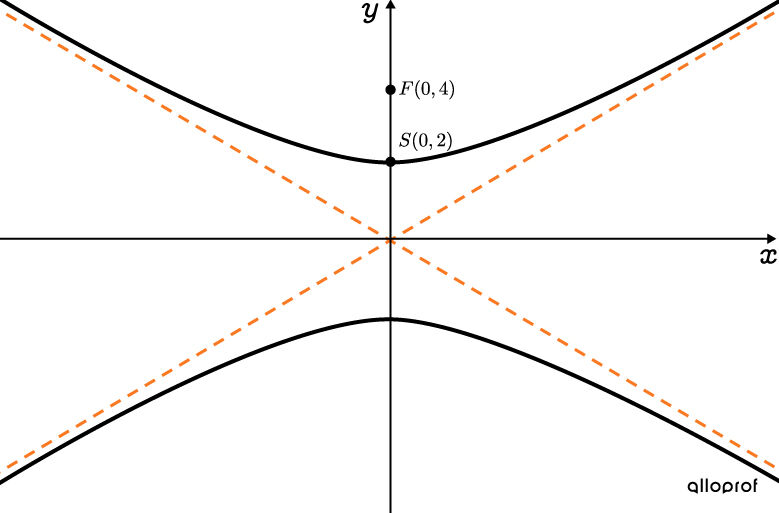
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole
Comme les sommets et les foyers sont placés à la verticale, l’hyperbole est verticale. On utilise l’équation suivante. ||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1|| -
Déterminer la valeur du paramètre |a| et/ou du paramètre |b|
Les coordonnées d’un sommet sont fournies. Comme l’hyperbole est verticale, on peut déterminer la valeur de |b.| ||\color{#3b87cd}{b}=\color{#3b87cd}{2}|| -
Déterminer le paramètre manquant
Comme les coordonnées du foyer sont fournies, on sait que |c=4.| Il faut utiliser le théorème de Pythagore pour déterminer la valeur de |a.| ||\begin{align}\color{#3a9a38}c^2&=\color{#ec0000}a^2+\color{#3b87cd}b^2\\ \color{#3a9a38}{4}^2&=\color{#ec0000}a^2+\color{#3b87cd}{2}^2\\16&=\color{#ec0000}a^2+4\\12&=\color{#ec0000}a^2\\\sqrt{12}&=\color{#ec0000}a\end{align}|| -
Écrire l’équation de l’hyperbole
En remplaçant la valeur des paramètres |a| et |b| dans l’équation de base, on obtient l'équation recherchée. ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}-\dfrac{y^2}{\color{#3b87cd}b^2}&=-1\\\dfrac{x^2}{\color{#ec0000}{\sqrt{12}}^2}-\dfrac{y^2}{\color{#3b87cd}2^2}&=-1\\ \dfrac{x^2}{12}-\dfrac{y^2}{4}&=-1 \end{align}||
Voici un exemple où le sommet et un couple |(x,y)| appartenant aux asymptotes sont fournis.
Détermine l’équation d’une hyperbole dont l’un des points sur l’axe transversal est |(-3,0)| et dont l’une de ses asymptotes passe par le point |\left(-2,\dfrac{10}{3}\right).|
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole
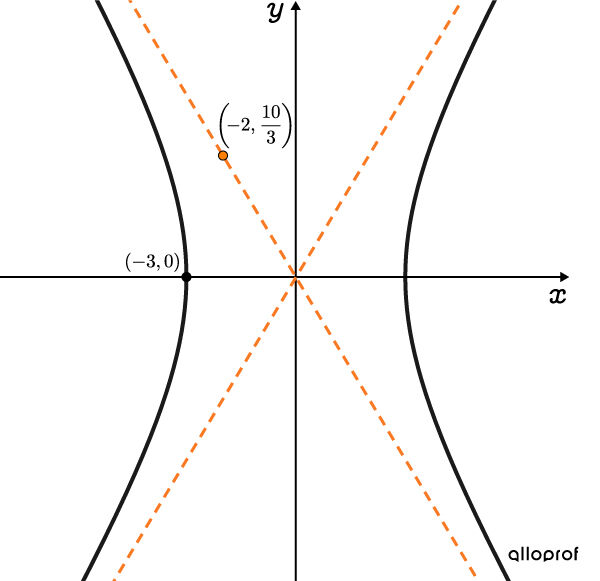
L’hyperbole est horizontale, car son axe transversal est horizontal. On utilise l’équation suivante. ||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1||
-
Déterminer la valeur du paramètre |a| et/ou du paramètre |b|
Puisque le point |(-3,0)| est placé sur l’axe transversal, il correspond à un sommet. Comme l’hyperbole est horizontale, on peut déterminer la valeur de |a.| ||\color{#ec0000}{a}=\color{#ec0000}{3}|| -
Déterminer le paramètre manquant
Comme les coordonnées d’un point appartenant à l’une des asymptotes sont fournies, on peut substituer toutes les informations dans l'équation de l’asymptote afin de déterminer la valeur de |b.| ||\begin{align}
y&=-\dfrac{\color{#3b87cd}b}{\color{#ec0000}a}x\\\\
\dfrac{10}{3}&=-\dfrac{\color{#3b87cd}b}{\color{#ec0000}3}(-2)\\\\
\dfrac{10}{3}&=\dfrac{2\color{#3b87cd}b}{3}\\\\
\color{#3b87cd}{5}&=\color{#3b87cd}b
\end{align}|| -
Écrire l’équation de l’hyperbole
En remplaçant la valeur des paramètres |a| et |b| dans l’équation de base, on obtient l'équation recherchée. ||\begin{align}
\dfrac{x^2}{\color{#ec0000}a^2}-\dfrac{y^2}{\color{#3b87cd}b^2}&=1\\\\
\dfrac{x^2}{\color{#ec0000}{3}^2}-\dfrac{y^2}{(\color{#3b87cd}{5})^2}&=1\\\\
\dfrac{x^2}{9}-\dfrac{y^2}{25}&=1
\end{align}||
Afin de tracer une hyperbole centrée à l’origine à l'aide de son équation, on peut suivre les étapes suivantes.
-
Placer le centre de l’hyperbole et déterminer son orientation.
-
Tracer le rectangle de l’hyperbole dont les sommets correspondent à : ||\begin{align}&R_1(-\color{#ec0000}a,\color{#3b87cd}b)&&R_2(\color{#ec0000}a,\color{#3b87cd}b)\\&R_3(-\color{#ec0000}a,-\color{#3b87cd}b)&&R_4(\color{#ec0000}a,-\color{#3b87cd}b)\end{align}||
-
Tracer les asymptotes en prolongeant les diagonales du rectangle.
-
Placer les sommets de l’hyperbole. ||\begin{align}\\ &\text{Hyperbole verticale}&&\text{Hyperbole horizontale}\\&S_1(0,\color{#3b87cd}b)&&S_1(-\color{#ec0000}a,0)\\&S_2(0,-\color{#3b87cd}b)&&S_2(\color{#ec0000}a,0)\end{align}||
-
Tracer l’hyperbole en passant par les sommets et en s’approchant des asymptotes, sans jamais y toucher.
Trace l’hyperbole représentée par l’équation suivante. ||\dfrac{x^2}{81}-\dfrac{y^2}{16}=-1||
-
Placer le centre de l’hyperbole et déterminer son orientation
Le centre de l’hyperbole centrée à l’origine est le point |(0,0).| Comme |1| est négatif dans la règle, on sait que l’hyperbole est verticale. -
Tracer le rectangle de l’hyperbole
À l’aide de la règle, on détermine les valeurs de |a| et de |b.| ||\begin{align}\color{#ec0000}{a}=\sqrt{81}&=\color{#ec0000}9\\\color{#3b87cd}{b}=\sqrt{16}&=\color{#3b87cd}4\end{align}|| Maintenant, on détermine les sommets du rectangle. ||\begin{align}&R_1(-\color{#ec0000}a,\color{#3b87cd}b)\Rightarrow (-\color{#ec0000}9,\color{#3b87cd}4)&&R_2(\color{#ec0000}a,\color{#3b87cd}b)\Rightarrow (\color{#ec0000}9,\color{#3b87cd}4)\\&R_3(-\color{#ec0000}a,-\color{#3b87cd}b)\Rightarrow (-\color{#ec0000}9,-\color{#3b87cd}4)&&R_4(\color{#ec0000}a,-\color{#3b87cd}b)\Rightarrow (\color{#ec0000}9,-\color{#3b87cd}4)\end{align}|| -
Tracer les asymptotes en prolongeant les diagonales du rectangle
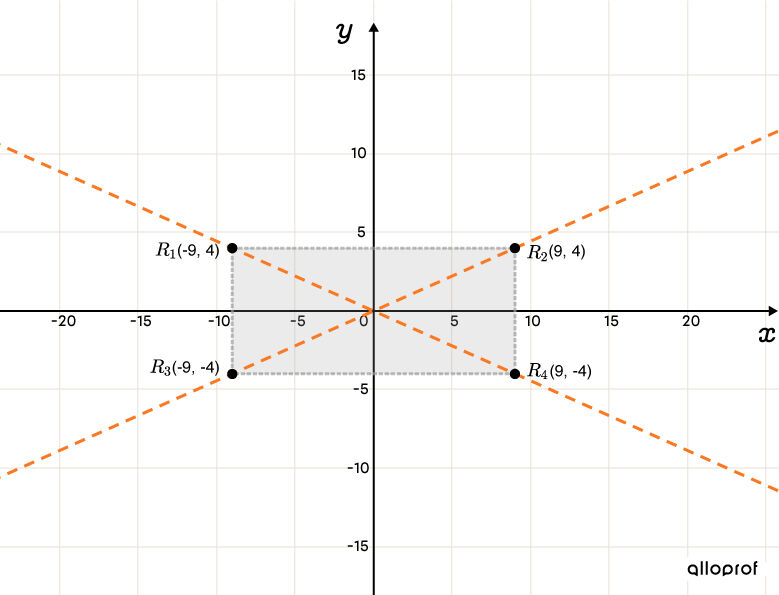
-
Placer les sommets de l’hyperbole
Puisque l’hyperbole est verticale, on détermine les sommets grâce à |b.| ||\begin{align}S_1(0,\color{#3b87cd}b)&\ \ \Rightarrow \ \ (0,\color{#3b87cd}4)\\S_2(0,-\color{#3b87cd}b)&\ \ \Rightarrow \ \ (0,-\color{#3b87cd}4)\end{align}|| -
Tracer l’hyperbole
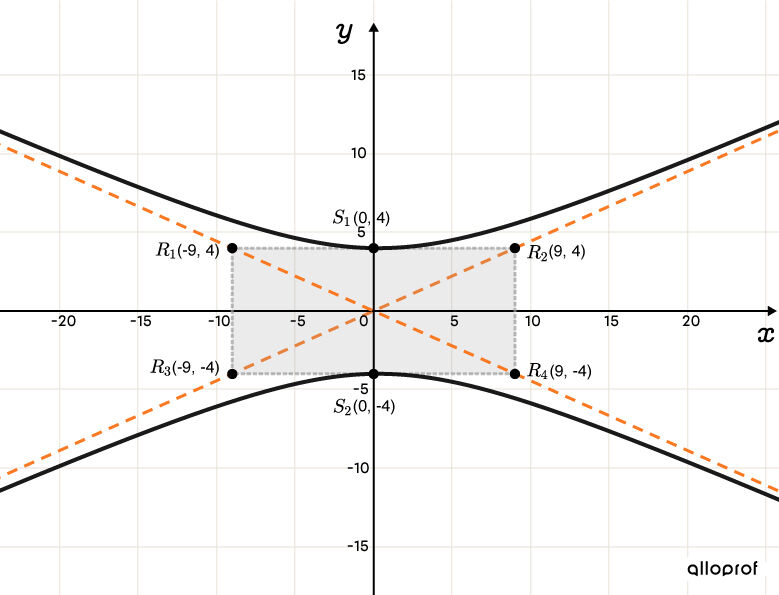
Voici une animation permettant de bien saisir les différentes relations et le rôle des paramètres dans l'hyperbole.
L'équation qui définit l’hyperbole transformée utilise les paramètres |a,| |b,| |h| et |k.| Comme pour l’hyperbole centrée à l’origine, on distingue 2 équations différentes selon son orientation. Il arrive aussi qu’on doive déterminer l’équation des droites constituant les asymptotes de la courbe.
Hyperbole verticale
||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=-1|| où ||\begin{align} a &:\text{la moitié de la largeur du rectangle}\\ b &: \text{la distance entre un sommet et le centre} \\ (h,k)&:\text{les coordonnées du centre}\\&\phantom {:}\ \ \text{(intersection des asymptotes)}\end{align}||
Hyperbole horizontale
||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=1|| où ||\begin{align} a &:\text{la mesure entre le sommet et le centre}\\ b &: \text{la moitié de la hauteur du rectangle} \\ (h,k)&:\text{les coordonnées du centre}\\&\phantom {:}\ \ \text{(intersection des asymptotes)}\end{align}||
Équation des asymptotes
||\begin{align}\text{Asymptote croissante :}\ \ y&=\dfrac{b}{a}(x-h)+k\\\\ \text{Asymptote décroissante :}\ \ y&=-\dfrac{b}{a}(x-h)+k\end{align}||
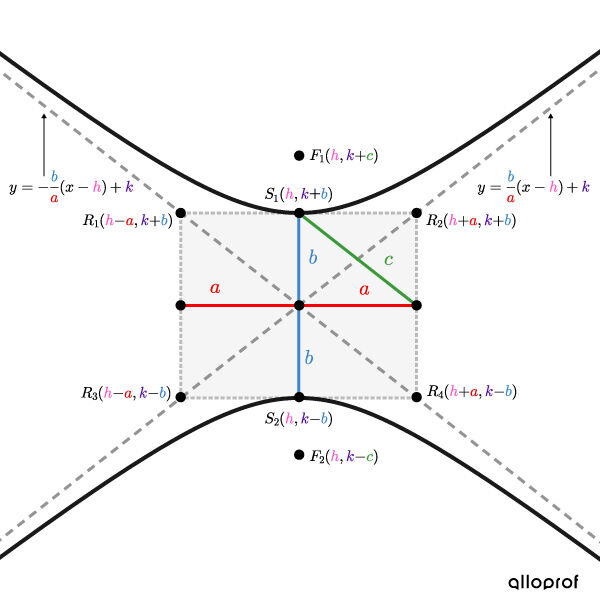
Voici les représentations graphiques des 2 types d’hyperboles non centrées à l’origine sur lesquelles sont placés les sommets, les foyers et les asymptotes.
Hyperbole verticale
Les points dont la différence des distances à 2 points fixes (foyers) est de |2\color{#3b87cd}b.|
Hyperbole horizontale
Les points dont la différence des distances à 2 points fixes (foyers) est de |2\color{#ec0000}a.|
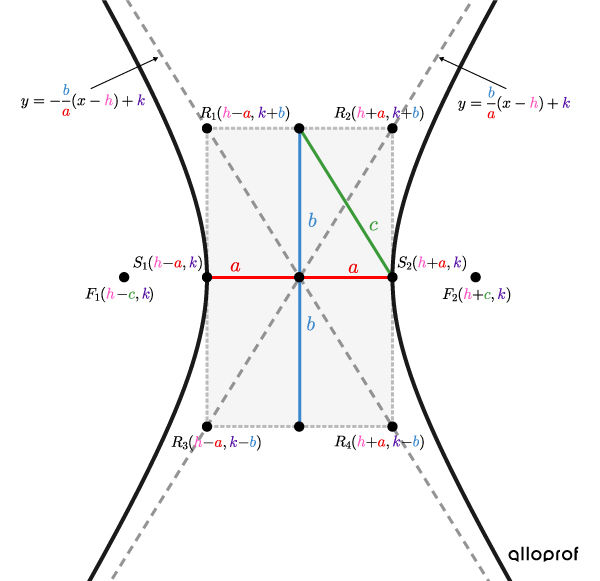
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
Afin de déterminer l'équation d'une hyperbole non centrée à l’origine à partir d'un graphique, il faut trouver la valeur des différents paramètres |a,| |b,| |h| et |k.|
Généralement, on utilise la démarche suivante.
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole.
-
Déterminer la valeur des paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| à partir des coordonnées du centre de l’hyperbole.
-
À l’aide des informations fournies par rapport aux sommets, déterminer la valeur du paramètre |\color{#ec0000}a| et/ou du paramètre |\color{#3B87CD}b| selon l’orientation de l’hyperbole.
-
Déterminer le paramètre manquant s’il y a lieu. Pour ce faire, utiliser l’une des stratégies suivantes :
a) Si le paramètre |\color{#3A9A38}c| (la distance entre le centre et un foyer) est fourni, utiliser le théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
b) Si un couple |(x,y)| appartenant à l’hyperbole est fourni, substituer toutes les informations dans l'équation de l’hyperbole.
c) Si un couple |(x,y)| appartenant à l’une des asymptotes est fourni, substituer toutes les informations dans l'équation de l’asymptote.
d) Si l’équation de l’une des asymptotes est fournie, utiliser le taux de variation |\dfrac{\color{#3b87cd}b}{\color{#ec0000}a}.|
-
Écrire l’équation de l’hyperbole.
Voici un exemple où le sommet et un couple |(x,y)| appartenant à l’hyperbole sont fournis.
Détermine l’équation de cette hyperbole.
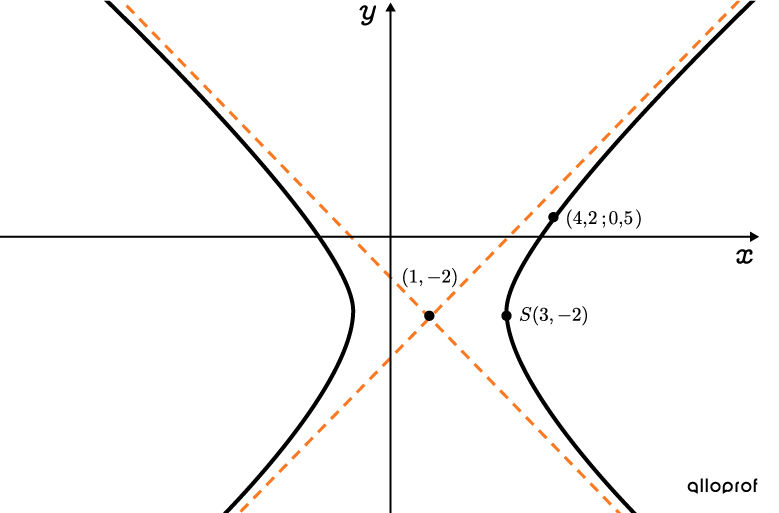
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole
L’hyperbole est horizontale. On utilise l’équation suivante. ||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=1|| -
Déterminer la valeur des paramètres |h| et |k| à partir des coordonnées du centre de l’hyperbole
L’hyperbole est centrée au point |(1,-2).| On obtient : ||\begin{align}\color{#ff55c3}h&=\color{#ff55c3}{1}\\ \color{#560fa5}k&=\color{#560fa5}{-2} \end{align}|| -
Déterminer la valeur du paramètre |a| et/ou du paramètre |b| selon l’orientation de l’hyperbole
Les coordonnées d’un sommet et du centre sont fournies. Comme l’hyperbole est horizontale, on peut déterminer la valeur de |a,| qui correspond à la distance entre le centre et le sommet. ||\color{#ec0000}a=3-1=\color{#ec0000}{2}|| -
Déterminer le paramètre manquant
Comme les coordonnées d’un point appartenant à l’hyperbole sont fournies, on substitue toutes les informations dans son équation afin de déterminer la valeur de |b.| ||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^{2}}-\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3B87CD}b^{2}}&=1\\ \dfrac{(4{,}2-\color{#ff55c3}1)^{2}}{\color{#ec0000}2^{2}}-\dfrac{\big(0{,}5-(\color{#560fa5}{-2})\big)^{2}}{\color{#3B87CD}b^{2}}&=1\\ \dfrac{10{,}24}{4}-\dfrac{6{,}25}{\color{#3B87CD}b^{2}}&=1\\ 2{,}56 - \dfrac{6{,}25}{\color{#3B87CD}b^{2}} &=1 \\ 1{,}56 &=\dfrac{6{,}25}{\color{#3B87CD}b^{2}}\\ \color{#3B87CD}b^{2}&=\dfrac{6{,}25}{1{,}56}\\ \color{#3B87CD}b^{2}&\approx4\\ \color{#3B87CD}b&\approx2 \end{align}|| -
Écrire l’équation de l’hyperbole
En remplaçant la valeur des paramètres dans l’équation de base, on obtient l'équation recherchée.||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}-\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}=1\\ \dfrac{(x-\color{#ff55c3}{1})^{2}}{\color{#ec0000}{2}^2}-\dfrac{\big(y-(\color{#560fa5}{-2})\big)^{2}}{\color{#3B87CD}{2}^2}=1\\ \dfrac{(x-1)^{2}}{4}-\dfrac{(y+2)^{2}}{4}=1 \end{align}||
Voici un exemple où un sommet et l’équation de l’une des asymptotes sont fournis.
Détermine l’équation d’une hyperbole verticale dont un des sommets est situé au point |(0,16)| et dont l’équation d’une asymptote est |y=\dfrac{6}{5}x-8.|
-
Choisir la bonne forme d’équation selon l’orientation de l’hyperbole
L’hyperbole est verticale. On utilise l’équation suivante.
||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=-1|| -
Déterminer la valeur des paramètres |h| et |k|
Puisque le sommet et le centre ont la même abscisse dans une hyperbole verticale, on connait la valeur de |h| et on peut déduire la valeur de |k.| ||\begin{align}
y&=\dfrac{6}{5}x-8\\
y&=\dfrac{6}{5}(x-\color{#ff55c3}h)+\color{#560fa5}{k}\\
y&=\dfrac{6}{5}(x-\color{#ff55c3}0)\color{#560fa5}{-8}\\\\
\color{#560fa5}{k}&=\color{#560fa5}{-8}
\end{align}|| Dans un plan cartésien, on peut placer approximativement le centre, le point fourni et les asymptotes croissantes et décroissantes.
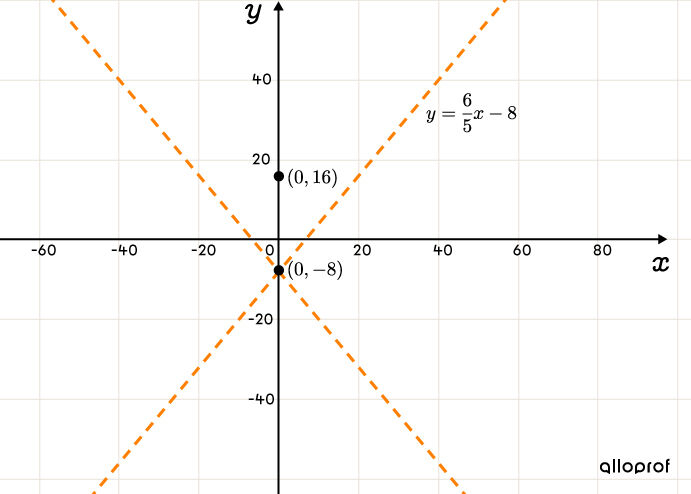
-
Déterminer la valeur du paramètre |a| et/ou du paramètre |b| selon l’orientation de l’hyperbole
On a les coordonnées d’un sommet et du centre. Comme l’hyperbole est verticale, on peut déterminer la valeur de |b,| qui correspond à la distance entre le centre et le sommet. ||\color{#3b87cd}{b}=16--8=\color{#3b87cd}{24}|| -
Déterminer le paramètre manquant
Il est possible de déterminer la valeur du paramètre |a| à l’aide de la pente de l’équation de l’asymptote qui correspond à |\dfrac{\color{#3b87cd}{b}}{\color{#ec0000}a}.| Ici, la pente est |\dfrac{6}{5}.| ||\begin{align}\dfrac{6}{5}&=\dfrac{\color{#3b87cd}{24}}{\color{#ec0000}a}\\\\\color{#ec0000}a&=\color{#ec0000}{20}\end{align}|| -
Écrire l’équation de l’hyperbole
En remplaçant la valeur des paramètres dans l’équation de base, on obtient l'équation recherchée. ||\begin{align}
\dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}-\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}=-1\\
\dfrac{(x-\color{#ff55c3}0)^{2}}{\color{#ec0000}{20}^2}-\dfrac{(y-(\color{#560fa5}{-8}))^{2}}{\color{#3B87CD}{24}^2}=-1\\
\dfrac{x^{2}}{400}-\dfrac{(y+8)^{2}}{576}=-1
\end{align}||
Afin de tracer une hyperbole non centrée à l’origine à l'aide de son équation, on peut suivre les étapes suivantes.
-
Identifier les paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| dans l'équation et placer le centre de l’hyperbole.
-
Tracer le rectangle de l’hyperbole dont les sommets correspondent à : ||\begin{align}&R_1(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b)&&R_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b)\\&R_3(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b)&&R_4(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b)\end{align}||
-
Tracer les asymptotes en prolongeant les diagonales du rectangle.
-
Placer les sommets de l’hyperbole. ||\begin{align}\\ &\text{Hyperbole verticale}&&\text{Hyperbole horizontale}\\&S_1(\color{#ff55c3}h,\color{#560fa5}k+\color{#3b87cd}b)&&S_1(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k)\\&S_2(\color{#ff55c3}h,\color{#560fa5}k-\color{#3b87cd}b)&&S_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k)\end{align}||
-
Tracer l’hyperbole en passant par les sommets et en s’approchant des asymptotes, sans jamais y toucher.
Trace l'hyperbole représentée par l'équation suivante. ||\dfrac{(x-5)^{2}}{64}-\dfrac{(y+4)^{2}}{100}=1||
-
Identifier les paramètres |h| et |k| dans l'équation et placer le centre de l’hyperbole
Selon l’équation, on détermine que le centre se situe aux coordonnées |(\color{#FF55C3}h, \color{#560fa5}k)=(\color{#FF55C3}5,\color{#560fa5}{-4}).|
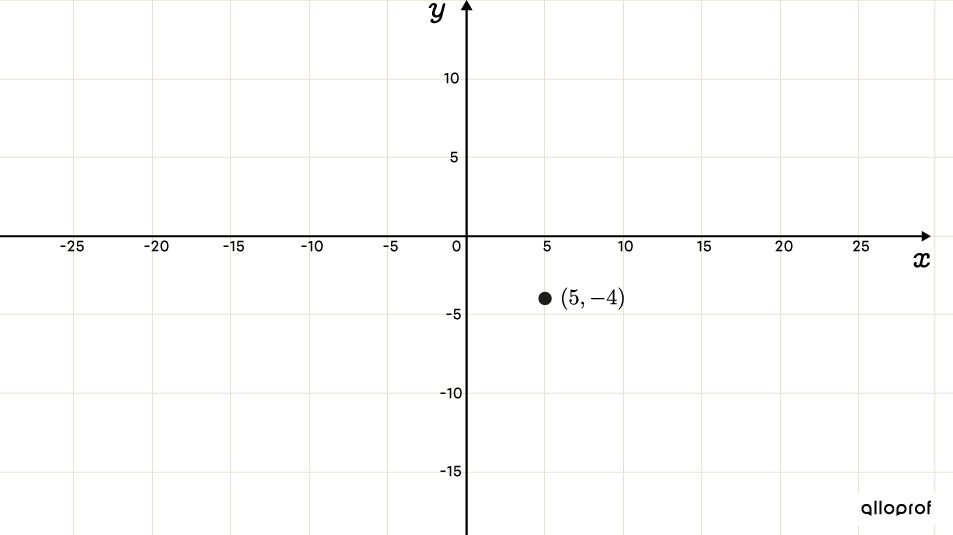
-
Tracer le rectangle de l’hyperbole
À l’aide de la règle, on détermine les valeurs de |a| et de |b.| ||\begin{align}\color{#ec0000}{a}&=\sqrt{64}=\color{#ec0000}8\\\color{#3b87cd}{b}&=\sqrt{100}=\color{#3b87cd}{10}\end{align}||Ensuite, on détermine les sommets du rectangle. ||\begin{align}&R_1(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b) &&R_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b) \\&R_1(\color{#ff55c3}5-\color{#ec0000}8,\color{#560fa5}{-4}+\color{#3b87cd}{10})\ \ && R_2(\color{#ff55c3}5+\color{#ec0000}8,\color{#560fa5}-4+\color{#3b87cd}{10})\\&R_1(-3,6)&&R_2(13,6)\end{align}|| ||\begin{align}&R_3(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b) &&R_4(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b) \\&R_3(\color{#ff55c3}5-\color{#ec0000}8,\color{#560fa5}{-4}-\color{#3b87cd}{10})\ \ && R_4(\color{#ff55c3}5+\color{#ec0000}8,\color{#560fa5}{-4}-\color{#3b87cd}{10})\\&R_3(-3,-14)&&R_4(13,-14)\end{align}|| -
Tracer les asymptotes en prolongeant les diagonales du rectangle
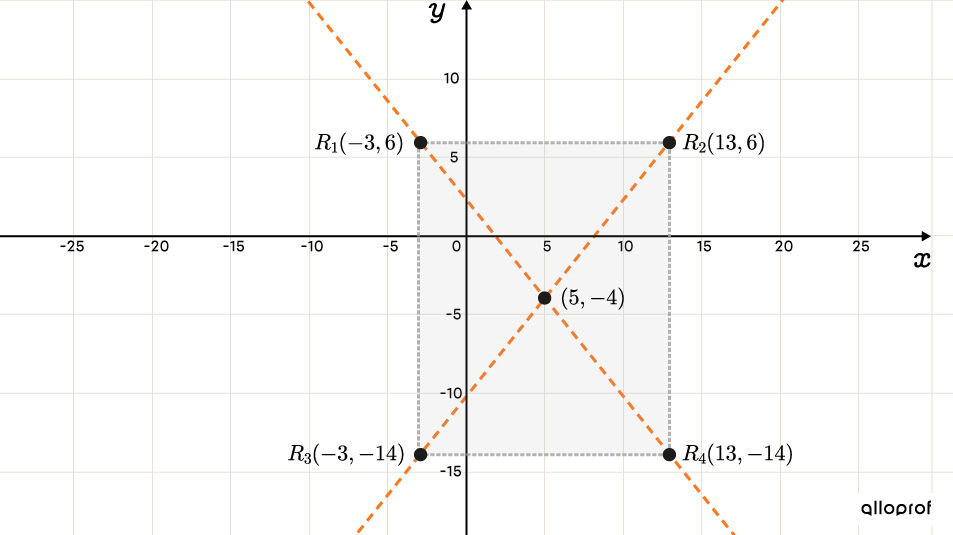
-
Placer les sommets de l’hyperbole
Puisque l’hyperbole est horizontale, on détermine les sommets grâce à |a.| ||\begin{align}S_1&(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k) &&S_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k)
\\S_1&(\color{#ff55c3}5-\color{#ec0000}8,\color{#560fa5}{-4}) &&S_2(\color{#ff55c3}5+\color{#ec0000}8,\color{#560fa5}-4) \\S_1&(-3,-4)&&S_2(13,-4)\end{align}|| -
Tracer l’hyperbole
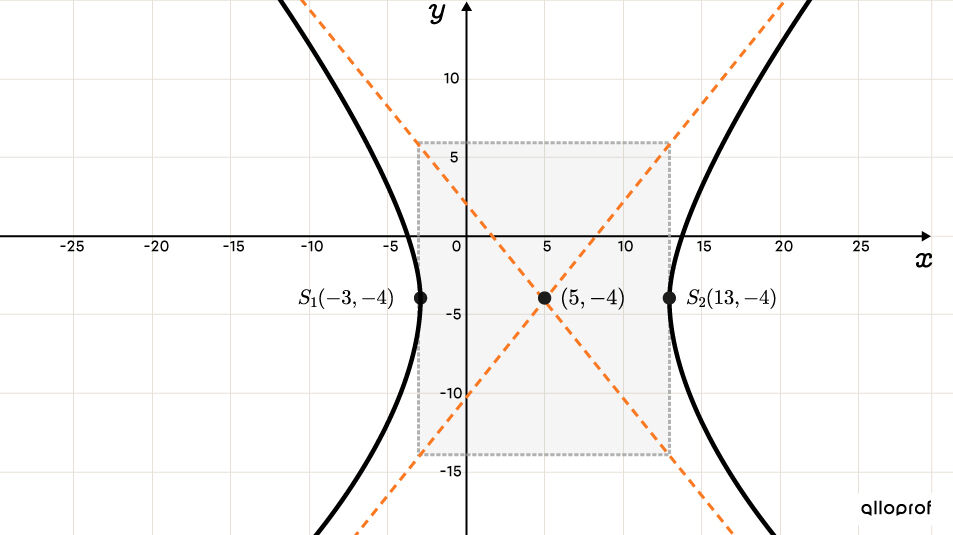
Lorsqu’on veut représenter une région délimitée par une hyperbole, on applique les relations suivantes.
| Hyperbole verticale | |
|---|---|
| Représentation graphique | Inéquation correspondante |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}>-1\\\\\dfrac{(x-h)^2}{a^2}&-\frac{(y-k)^2}{b^2}>-1\end{align}|| |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}<-1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}<-1\end{align}|| |
| Hyperbole horizontale | |
| Représentation graphique | Inéquation correspondante |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}<1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}<1\end{align}|| |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}>1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}>1\end{align}|| |
Si on veut inclure les points qui sont sur l'hyperbole, on change respectivement les symboles d'inéquations |<, >| pour les symboles |\geq , \leq.|