L’ellipse fait partie des coniques. Elle s’obtient par l’intersection d’une surface conique et d’un plan.
Une ellipse est le lieu géométrique de tous les points dont la somme des distances à 2 points fixes, appelés foyers, est constante.
-
L'ellipse possède 2 axes de symétrie. Le plus long se nomme le grand axe et le plus court, le petit axe.
-
L'ellipse possède 2 foyers, |F_1| et |F_2.|
-
L'ellipse possède 4 sommets, |S_1,| |S_2,| |S_3| et |S_4.|
-
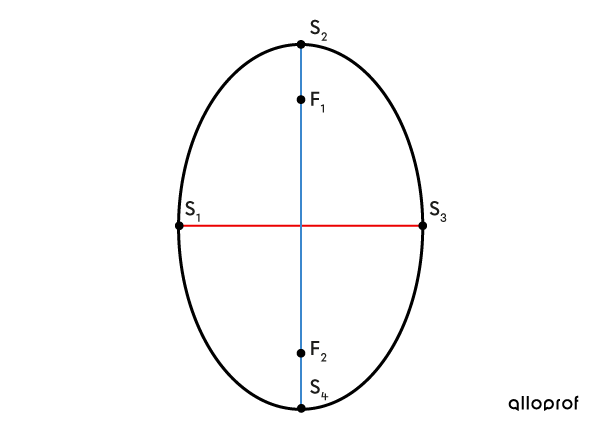
L'ellipse peut être verticale ou horizontale.
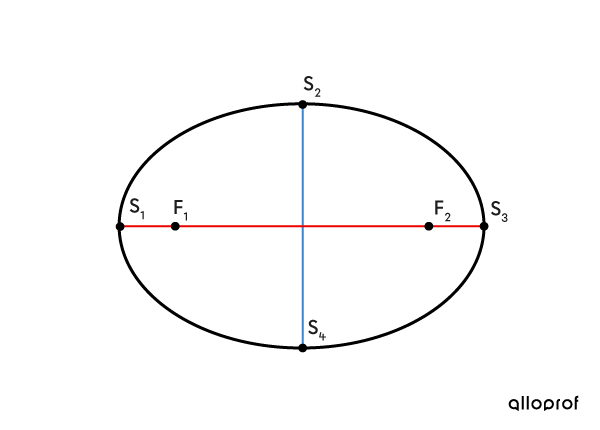
L'équation qui définit l'ellipse centrée à l’origine utilise les paramètres |a| et |b.|
||\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1||où||\begin{align} a &:\text{Demi-mesure de l'axe horizontal}\\ b &: \text{Demi-mesure de l'axe vertical} \end{align}||
-
Si |\color{#ec0000}a < \color{#3b87cd}b,| l'ellipse est verticale.
-
Si |\color{#ec0000}a > \color{#3b87cd}b,| l'ellipse est horizontale.
Voici les représentations graphiques des 2 types d’ellipses sur lesquelles sont placés les points importants et leurs coordonnées en fonction des relations qui établissent leurs paramètres.
Ellipse verticale
La somme des distances d'un point de l'ellipse verticale par rapport à chacun des foyers est de |2\color{#3b87cd}b.|
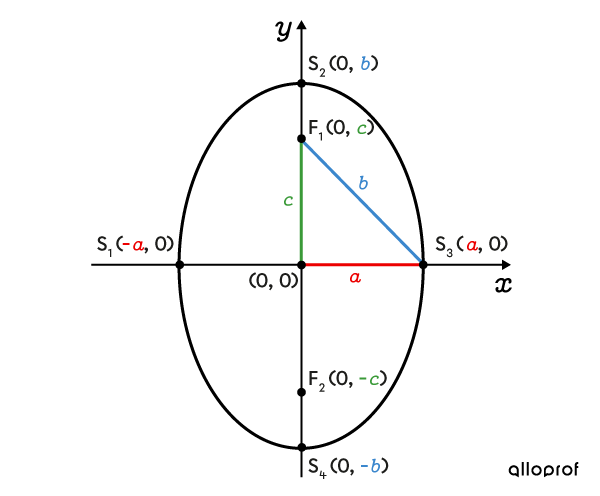
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||
Ellipse horizontale
La somme des distances d'un point de l'ellipse horizontale par rapport à chacun des foyers est de |2\color{#ec0000}a.|
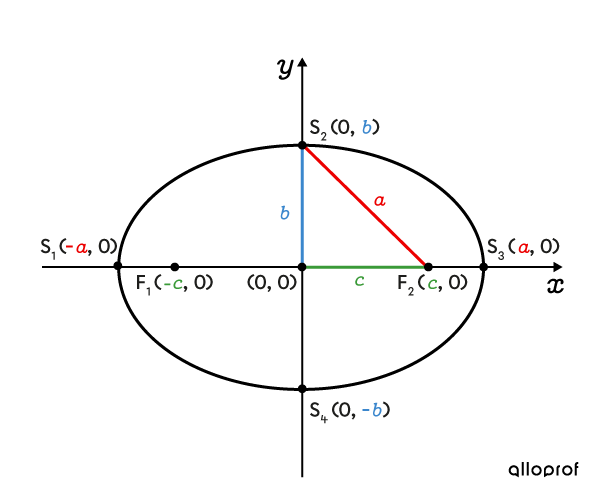
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||
Pour déterminer l'équation d'une ellipse centrée, il faut trouver la valeur des paramètres |a| et |b.|
Généralement, on utilise la démarche suivante.
-
Déterminer la valeur du paramètre |\color{#ec0000}a,| qui correspond à la moitié de l'axe horizontal de l'ellipse, et/ou du paramètre |\color{#3B87CD}b,| qui correspond à la moitié de l'axe vertical.
-
S’il manque un des deux paramètres, le déduire à l’aide d’une des stratégies suivantes :
a) Si le paramètre |\color{#3A9A38}c| (la distance entre le centre et un foyer) est fourni, utiliser le théorème de Pythagore afin de déterminer la valeur du paramètre manquant. ||\begin{align}\text{Ellipse verticale :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Ellipse horizontale :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||
b) Si un couple |(x,y)| est fourni, substituer toutes les informations dans l'équation et déterminer la valeur du paramètre manquant.
-
Écrire l'équation de l'ellipse.
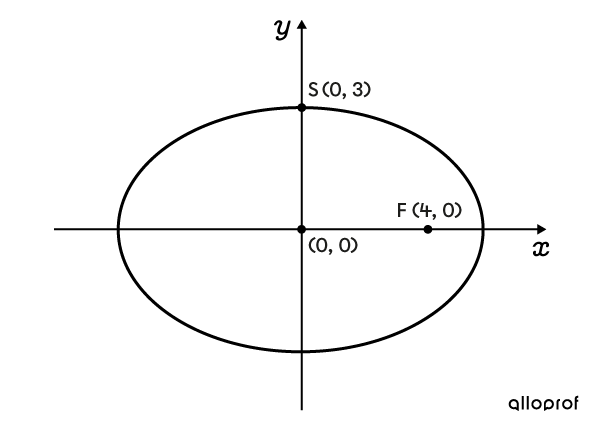
Détermine l’équation de cette ellipse.
-
Déterminer la valeur des paramètres |a| et/ou |b|
On connait les coordonnées de l'un des sommets |S(0,3),| ce qui nous permet de déterminer |b.| On obtient : ||\color{#3b87cd}b=\color{#3b87cd}3|| -
Déduire le paramètre manquant
On connait aussi les coordonnées de l'un des foyers, |F(4,0).| On l'utilise pour déterminer |c,| qui correspond à la distance entre le centre et un foyer. On obtient : ||\color{#3a9a38}c=\color{#3a9a38}4|| Puisque l’ellipse est horizontale et que les paramètres |b| et |c| sont connus, on utilise le théorème de Pythagore pour trouver la valeur de |a.| On obtient : ||\begin{align}\color{#3a9a38}c^2&=\color{#ec0000}a^2-\color{#3b87cd}b^2\\\color{#3a9a38}4^2&=\color{#ec0000}a^2-\color{#3b87cd}3^2\\16&=\color{#ec0000}a^2-9\\25&=\color{#ec0000}a^2\\\color{#ec0000}5&=\color{#ec0000}a\end{align}|| -
Écrire l'équation de l'ellipse
En remplaçant la valeur des paramètres |a| et |b| dans l’équation de base, on trouve l'équation recherchée. ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=1\\ \dfrac{x^2}{\color{#ec0000}{5}^2}+\dfrac{y^2}{\color{#3B87CD}{3}^2}=1\\ \dfrac{x^2}{25}+\dfrac{y^2}{9}=1\end{align}||
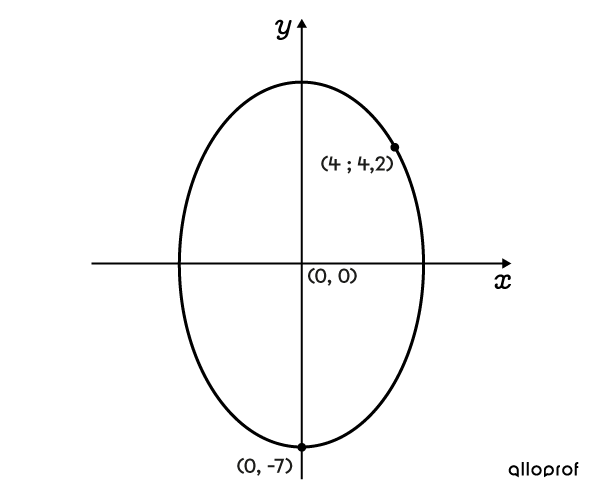
Détermine l’équation de cette ellipse.
-
Déterminer la valeur des paramètres |a| et/ou |b|
On connait les coordonnées de l'un des sommets, |S(0,-7)|, sur l’axe vertical. On l'utilise pour déterminer |b.| On obtient : ||\color{#3b87cd}b=\color{#3b87cd}7|| -
Déduire le paramètre manquant
On connait aussi les coordonnées d'un point, |P(4;4{,}2).| Dans l’équation, on remplace |b| par |7,| |x| par |4| et |y| par |4{,}2,| puis on isole le paramètre |a.| ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=&\ 1\\ \dfrac{4^2}{\color{#ec0000}{a}^2}+\dfrac{4{,}2^2}{\color{#3B87CD}{7}^2}=&\ 1\\ \dfrac{16}{\color{#ec0000}{a}^2}+\dfrac{17{,}64}{49}=&\ 1 \\\dfrac{16}{\color{#ec0000}{a}^2}+0{,}36=&\ 1 \\ \dfrac{16}{\color{#ec0000}{a}^2}=&\ 0{,}64 \\ 25=&\ \color{#ec0000}{a}^2\\ \color{#ec0000}{5}=&\ \color{#ec0000}a \end{align}|| -
Écrire l'équation de l'ellipse
En remplaçant la valeur des paramètres |a| et |b| dans l’équation de base, on trouve l'équation recherchée. ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=1\\ \dfrac{x^2}{\color{#ec0000}{5}^2}+\dfrac{y^2}{\color{#3B87CD}{7}^2}=1\\ \dfrac{x^2}{25}+\dfrac{y^2}{49}=1\end{align}||
Pour tracer une ellipse centrée à l'aide de son équation, on peut suivre les étapes suivantes.
-
Placer le centre de l’ellipse.
-
Placer les 2 sommets situés sur l’axe horizontal à l’aide de la valeur du paramètre |\color{#EC0000}a.| Voici les coordonnées des sommets. ||\begin{align}S_1&=(\color{#EC0000}{-a},0)\\ S_3&=(\color{#EC0000}a,0)\end{align}||
-
Placer les 2 sommets situés sur l’axe vertical à l’aide de la valeur du paramètre |\color{#3B87CD}b.| Voici les coordonnées des sommets. ||\begin{align}S_2&=(0,\color{#3B87CD}b)\\ S_4&=(0,\color{#3B87CD}{-b})\end{align}||
-
Tracer l'ellipse en reliant les 4 sommets.
Trace l'ellipse représentée par l'équation suivante. ||\dfrac{x^{2}}{289}+\dfrac{y^{2}}{196}=1||
-
Placer le centre de l’ellipse
Dans l’ellipse centrée à l’origine, le centre est le point |(0,0).| -
Placer les 2 sommets sur l’axe horizontal
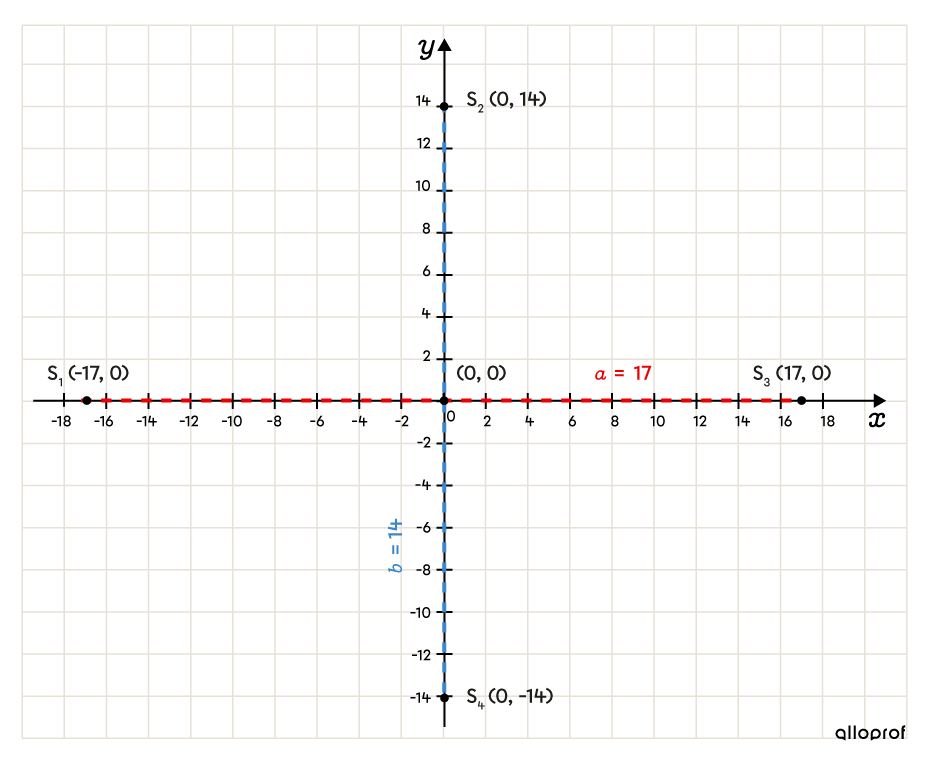
On a |\color{#ec0000}{a}=\sqrt{289}=\color{#ec0000}{17}.| On place les 2 sommets. ||\begin{align}S_1=&\ (-17,0)\\S_3=&\ (17,0)\end{align}|| -
Placer les 2 sommets sur l’axe vertical
On a |\color{#3b87cd}b=\sqrt{196}=\color{#3b87cd}{14}.| On place les 2 sommets. ||\begin{align}S_2=&\ (0,14)\\S_4=&\ (0,-14)\end{align}||
-
Tracer l'ellipse
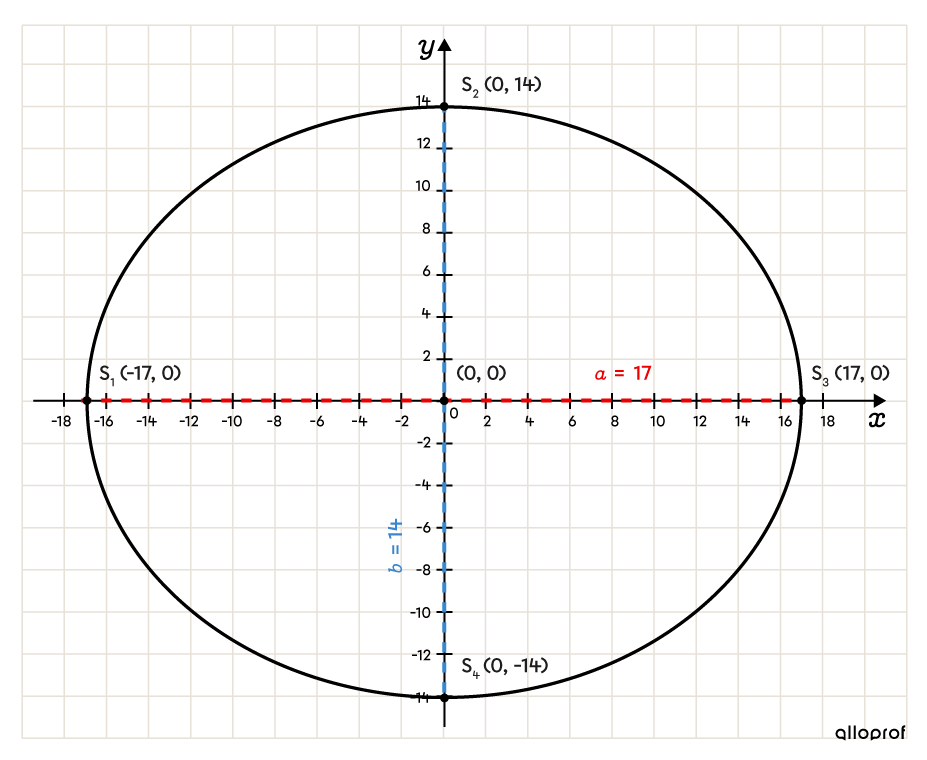
L'équation qui définit l'ellipse non centrée utilise les paramètres |a,| |b,| |h| et |k.|
||\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|| où ||\begin{align} a &:\text{Demi-mesure de l'axe horizontal}\\ b &: \text{Demi-mesure de l'axe vertical}\\ (h,k) & : \text{Coordonnées du centre de l'ellipse}\end{align}||
-
Si |\color{#ec0000}a < \color{#3b87cd}b,| l'ellipse est verticale.
-
Si |\color{#ec0000}a > \color{#3b87cd}b,| l'ellipse est horizontale.
Ellipse verticale
La somme des distances d'un point de l'ellipse verticale par rapport à chacun des foyers est de |2\color{#3b87cd}b.|
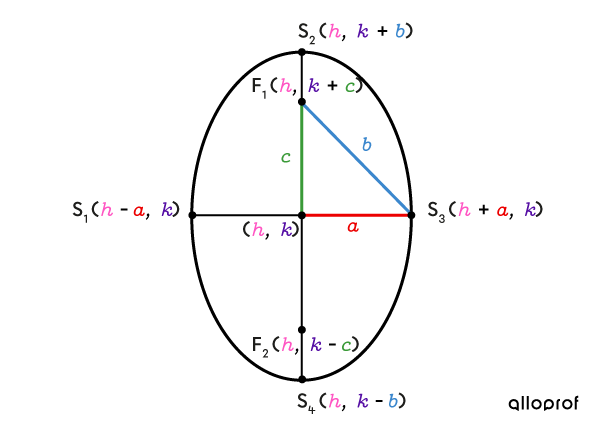
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||
Ellipse horizontale
La somme des distances d'un point de l'ellipse horizontale par rapport à chacun des foyers est de |2\color{#ec0000}a.|
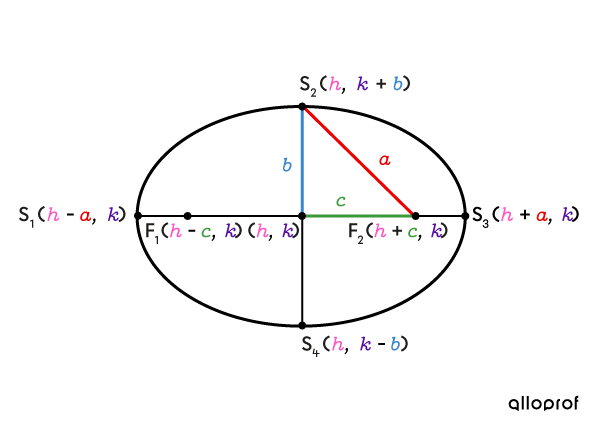
La relation entre les mesures |\color{#ec0000}a,| |\color{#3b87cd}b| et |\color{#3a9a38}c| peut être exprimée à l’aide du théorème de Pythagore. ||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||
Pour déterminer l'équation d'une ellipse non centrée à partir d'un graphique, il faut trouver la valeur des paramètres |a,| |b,| |h| et |k.|
Généralement, la démarche ressemble à celle-ci.
-
Déterminer la valeur des paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| à partir des coordonnées du centre de l'ellipse.
-
Déterminer la valeur du paramètre |\color{#ec0000}a,| qui correspond à la moitié de l'axe horizontal de l'ellipse, et/ou du paramètre |\color{#3B87CD}b,| qui correspond à la moitié de l'axe vertical.
-
S’il manque un des 2 paramètres |a| ou |b,| le déduire à l’aide d’une des stratégies suivantes :
a) Si le paramètre |\color{#3A9A38}c| (la distance entre le centre et un foyer) est fourni, utiliser le théorème de Pythagore et déterminer la valeur du paramètre manquant. ||\begin{align}\text{Ellipse verticale :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Ellipse horizontale :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||
b) Si un couple |(x,y)| est fourni, substituer toutes les informations dans l'équation et déterminer la valeur du paramètre manquant.
-
Écrire l’équation de l’ellipse.
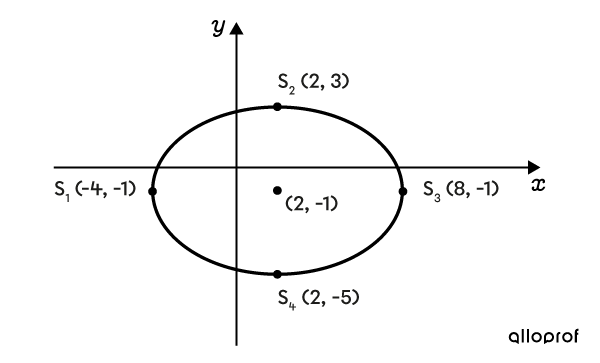
Détermine l’équation de cette ellipse.
-
Déterminer la valeur des paramètres |h| et |k|
L’ellipse est centrée au point |(2,-1),| on a donc les paramètres |h| et |k| suivants. ||\begin{align} \color{#ff55c3}{h}&=\color{#ff55c3}{2}\\ \color{#560fa5}{k}&=\color{#560fa5}{-1} \end{align}|| -
Déterminer la valeur des paramètres |a| et |b|
On connait la valeur de chacun des sommets de l'ellipse. On peut déterminer directement la valeur de |a| et de |b,| qui correspond respectivement à la demi-mesure de l'axe horizontal et de l'axe vertical.
Comme l'axe horizontal mesure |12| unités et que l'axe vertical mesure |8| unités, on obtient les paramètres |a| et |b| suivants. ||\begin{align} \color{#ec0000}{a}&=\color{#ec0000}{6}\\ \color{#3b87cd}{b}&=\color{#3b87cd}{4} \end{align}|| -
Déterminer la valeur des paramètres manquants
Pour cet exemple, on a toutes les informations nécessaires pour écrire l'équation. -
Écrire l'équation de l'ellipse
En remplaçant la valeur des paramètres dans l’équation de base, on trouve l'équation recherchée. ||\begin{align}\dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}=1\\
\dfrac{(x-\color{#ff55c3}{2})^{2}}{\color{#ec0000}{6}^2}+\dfrac{(y-(\color{#560fa5}{-1}))^{2}}{\color{#3B87CD}{4}^2}=1\\
\dfrac{(x-2)^{2}}{36}+\dfrac{(y+1)^{2}}{16}=1\end{align}||
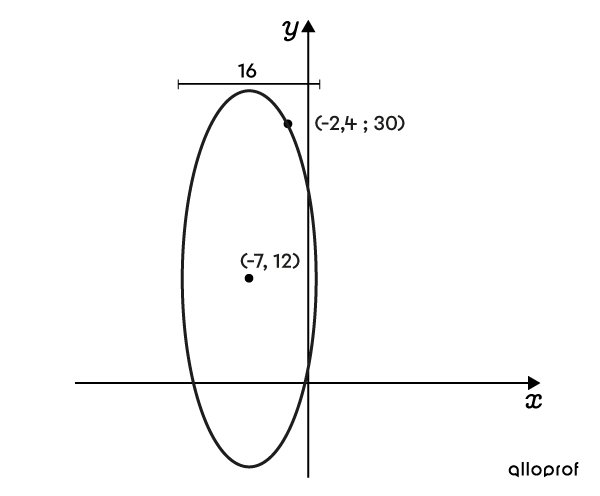
Détermine l’équation de cette ellipse, sachant que son axe horizontal mesure |16| unités.
-
Déterminer la valeur des paramètres |h| et |k|
L’ellipse est centrée au point |(-7,12),| on a donc les paramètres |h| et |k| suivants. ||\begin{align} \color{#ff55c3}{h}&=\color{#ff55c3}{-7}\\ \color{#560fa5}{k}&=\color{#560fa5}{12} \end{align}|| -
Déterminer la valeur des paramètres |a| et |b|
On connait la longueur de l’axe horizontal. On peut donc déterminer directement la valeur de |a.|
Comme l'axe horizontal mesure |16| unités, on obtient le résultat suivant. ||\color{#ec0000}{a}=\color{#ec0000}{8}|| -
Déterminer la valeur des paramètres manquants
Il nous manque seulement la valeur de |b.| On utilise le point |(-2{,}4;30)| pour la trouver en substituant ce point dans l’équation. ||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}&=1\\ \dfrac{(-2{,}4-(\color{#ff55c3}{-7}))^{2}}{\color{#ec0000}{8}^2}+\dfrac{(30-\color{#560fa5}{12})^{2}}{\color{#3B87CD}{b}^2}&=1\\ \dfrac{21{,}16}{64}+\dfrac{324}{\color{#3B87CD}b^2}&=1\\ \dfrac{529}{1\ 600}+\dfrac{324}{\color{#3B87CD}b^2}&=1\\ \dfrac{324}{\color{#3B87CD}b^2}&=\dfrac{1\ 071}{1\ 600}\\ 1\ 071\color{#3B87CD}b^2&=518\ 400\\ \color{#3B87CD}{b}^2&\approx484{,}03\\ \color{#3b87cd}{b}&\approx\color{#3b87cd}{22} \end{align}|| -
Écrire l'équation de l'ellipse
En remplaçant la valeur des paramètres dans l’équation de base, on trouve l'équation recherchée. ||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}&=1\\ \dfrac{(x-(\color{#ff55c3}{-7}))^{2}}{\color{#EC0000}{8}^2}+\dfrac{(y-\color{#560fa5}{12})^{2}}{\color{#3b87cd}{22}^2}&=1\\ \dfrac{(x+7)^{2}}{64}+\dfrac{(y-12)^{2}}{484}&=1\\ \end{align}||
Pour tracer une ellipse à l'aide de son équation, on peut suivre les étapes suivantes.
-
Identifier les paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| dans l'équation et placer le centre de l’ellipse.
-
Placer les 2 sommets situés sur l’axe horizontal à l’aide de la valeur du paramètre |\color{#EC0000}a.| Voici les coordonnées des sommets. ||\begin{align}S_1:(\color{#FF55C3}h\color{#EC0000}{-a},\color{#560FA5}k)\\ S_3:(\color{#FF55C3}h\color{#EC0000}{+a},\color{#560FA5}k)\end{align}||
-
Placer les 2 sommets sur l’axe vertical à l’aide de la valeur du paramètre |\color{#3B87CD}b.| Voici les coordonnées des sommets. ||\begin{align}S_2:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{+b})\\ S_4:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{-b})\end{align}||
-
Tracer l'ellipse en reliant les 4 sommets.
Trace l'ellipse représentée par l'équation suivante. ||\dfrac{(x-5)^{2}}{64}+\frac{(y+4)^{2}}{100}=1||
-
Identifier les paramètres |h| et |k| dans l'équation et placer le centre
Selon l’équation, on détermine que le centre se situe aux coordonnées suivantes. ||(\color{#FF55C3}h,\color{#560fa5}k)=(\color{#FF55C3}5,\color{#560fa5}{-4})||
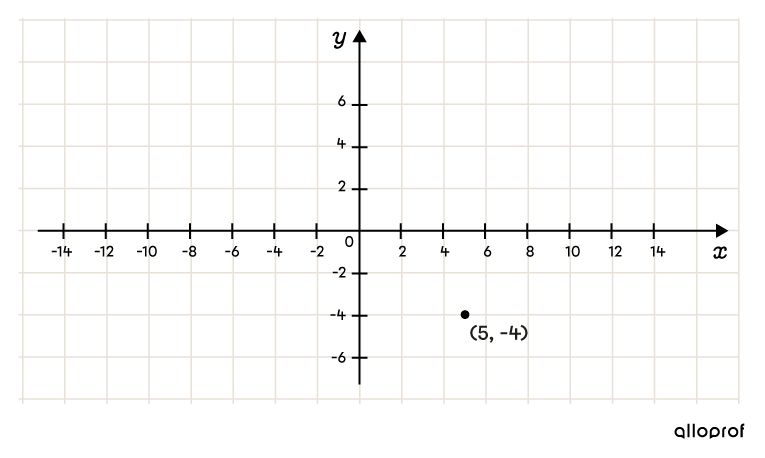
-
Placer les 2 sommets sur l’axe horizontal
On a |\color{#ec0000}{a}=\sqrt{64}=\color{#ec0000}{8}.| On place les 2 sommets. ||\begin{align}S_1=&\ (\color{#FF55C3}5\color{#EC0000}{-8},\color{#560FA5}{-4})= (-3,-4)\\ S_3=&\ (\color{#FF55C3}5\color{#EC0000}{+8},\color{#560FA5}{-4})=(13,-4)\end{align}|| -
Placer les 2 sommets sur l’axe vertical
On a |\color{#3B87CD}{b}=\sqrt{100}=\color{#3B87CD}{10}.| On place les 2 sommets. ||\begin{align}S_2=&\ (\color{#FF55C3}5,\color{#560FA5}{-4}\color{#3B87CD}{+10})= (5,6)\\ S_4=&\ (\color{#FF55C3}5,\color{#560FA5}{-4}\color{#3B87CD}{-10})=(5,-14)\end{align}||
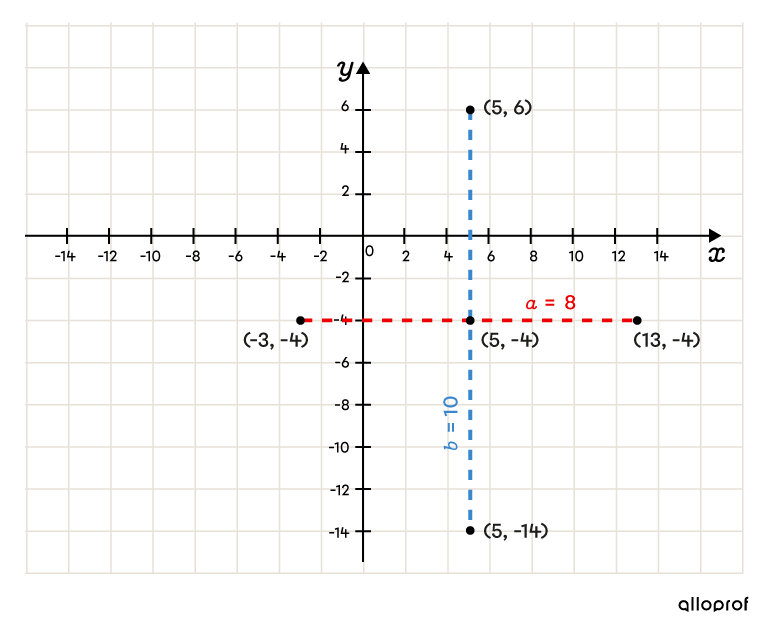
-
Tracer l'ellipse
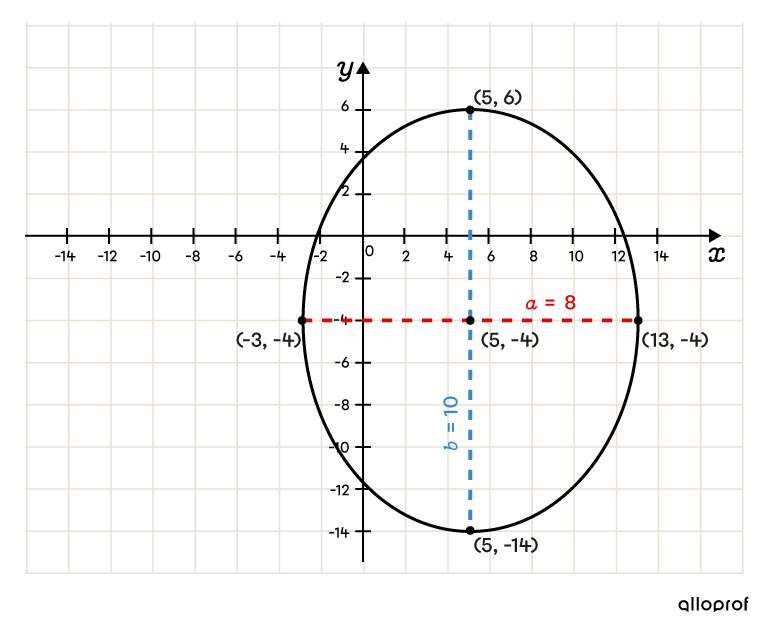
Lorsqu’on veut représenter une région délimitée par une ellipse, on applique les relations suivantes.
| Secteur du plan | Représentation graphique |
Inéquation correspondante |
|---|---|---|
|
L'extérieur, excluant la courbe |
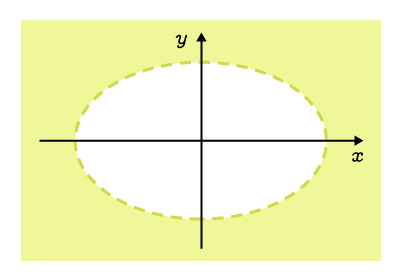 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}>1\\\\ |
|
L'intérieur, excluant la courbe |
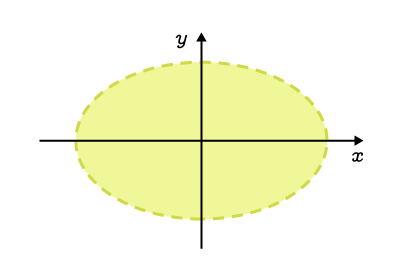 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}<1\\\\ |
|
L'extérieur, incluant la courbe |
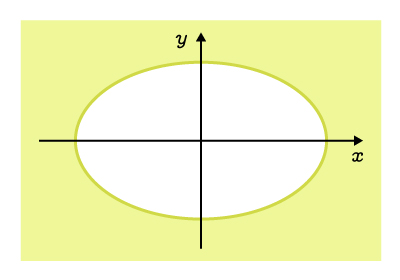 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\geq1\\\\ |
|
L'intérieur, incluant la courbe |
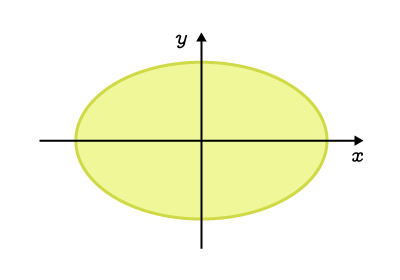 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\leq1\\\\ |
L'équation générale de toutes les coniques, dont l'ellipse, pour lesquelles l'axe horizontal est parallèle à l'axe des abscisses et l'axe vertical est parallèle à l'axe des ordonnées est : || Ax^2+ By^2+Cx+Dy+E=0||
Passer de la forme générale à la forme canonique peut être utile pour résoudre certains problèmes concernant l'ellipse.
Détermine la distance focale (distance entre les 2 foyers) de l’ellipse représentée par l’équation suivante. ||x^2+9y^2 + 8x - 18y - 56 = 0||
-
Factoriser l’équation à l'aide de la complétion de carré
On regroupe les termes partageant la même variable. ||\color{#3a9a38}{x^2+8x}+\color{#3B87CD}{9y^2-18y}-56=0|| On effectue les complétions de carré.
Pour les termes en |x,| on a l’équation suivante. ||\begin{align} \color{#3a9a38}{x^2+8x}&=(x)^2+2(x)(4)\color{#fa7921}{+(4)^2-(4)^2}\\ \color{#3a9a38}{x^2+8x}&=\color{#3a9a38}{(x+4)^2-16} \end{align}||
Quant aux termes en |y,| on a l’équation suivante. ||\begin{align}\color{#3B87CD}{9y^2-18y}&=9\Big(y^2-2y\Big)\\ \color{#3B87CD}{9y^2-18y}&=9\Big((y)^2-2(y)(1)\color{#fa7921}{+(1)^2-(1)^2}\Big)\\ \color{#3B87CD}{9y^2-18y}&=9\Big((y-1)^2-1\Big)\\ \color{#3B87CD}{9y^2-18y}&=\color{#3B87CD}{9(y-1)^2-9}\\ \end{align}|| On remplace les termes en |x| et en |y| dans l'équation de départ et on réduit les termes constants. ||\begin{align} \color{#3a9a38}{x^2+8x}+\color{#3B87CD}{9y^2-18y}-56&=0\\ \color{#3a9a38}{(x+4)^2-16}+\color{#3B87CD}{9(y-1)^2-9}-56&=0\\ (x+4)^2+9(y-1)^2-81&=0\\ \end{align}|| -
Effectuer les manipulations pour trouver l’équation canonique
Comme la forme canonique de l’ellipse est égale à |1|, on doit faire quelques manipulations. ||\begin{align} (x+4)^2+9(y-1)^2-81&=0\\ (x+4)^2+9(y-1)^2&=81\\ \dfrac{(x+4)^2}{81}+\dfrac{9(y-1)^2}{81}&=\dfrac{81}{81} \\ \dfrac{(x+4)^2}{81}+\frac{(y-1)^2}{9}&=1\\ \end{align}|| -
Trouver les valeurs de |a| et de |b|
Puisqu’on cherche la distance focale, il faut trouver la valeur de |a| et de |b.| Pour y arriver, on extrait les racines carrées aux 2 dénominateurs. ||\begin{align} \dfrac{(x+4)^2}{81} + \dfrac{(y-1)^2}{9} &=1\\ \dfrac{(x+4)^2}{\color{#ec0000}9^2} + \dfrac{(y-1)^2}{\color{#3b87cd}3^2} &=1\end{align}|| -
Calculer la valeur de |c|
Comme |a > b,| on utilise l'équation suivante. ||\begin{align}\color{#3a9a38}c^2&=\color{#ec0000}a^2-\color{#3b87cd}b^2\\ \color{#3a9a38}c^2&= \color{#ec0000}9^2-\color{#3b87cd}3^2\\ \color{#3a9a38}c^2&=81-9\\ \color{#3a9a38}c^2&=72\\ \color{#3a9a38}c\ &\approx \color{#3a9a38}{8{,}5}\end{align}||
La distance focale de cette ellipse est donc de |2 \times 8{,}5 = 17.|