Pour réussir à calculer une mesure manquante dans un solide décomposable ou dans un solide tronqué à partir du volume, il faut créer une équation et la résoudre. Pour ce faire, les formules permettant le calcul du volume des solides sont utiles. Voici une présentation globale de la démarche à utiliser.
-
Déterminer le volume avec lequel il faut travailler.
-
Identifier la mesure manquante avec une variable.
-
Associer au volume de chaque solide une valeur numérique ou une expression algébrique.
-
Créer une équation en fonction du contexte.
-
Résoudre l'équation.
-
Interpréter la réponse selon le contexte.
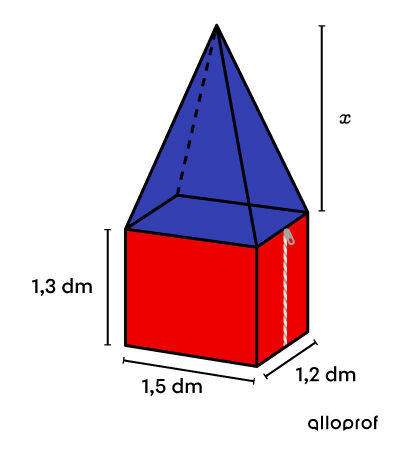
Une fois fermée, une boite à lunch a l'allure suivante :

En moyenne, l'espace disponible à l'intérieur d'une boite à lunch est de |3{,}65 \ \text{dm}^3.| Ainsi, quelle devrait être la hauteur totale de la boite à lunch pour respecter ce standard?
-
Déterminer le volume
Il est indiqué que le volume total est de |3{,}65 \ \text{dm}^3.| -
Identifier la mesure manquante avec une variable
La hauteur de la pyramide n’est pas donnée. Comme elle doit être prise en compte lors du calcul du volume, on lui associe la variable |x.|
-
Associer au volume de chaque solide une valeur numérique ou une expression algébrique
||\begin{align} \color{#333fb1}{V_\text{pyramide}} &=\dfrac{A_b\times h}{3}\\&= \frac{1{,}5 \times 1{,}2 \times x}{3} \\ &= \color{#333fb1}{0{,}6x\ \text{dm}^3} \\\\ \color{#ec0000}{V_\text{prisme}} &=A_b\times h\\&= 1{,}5 \times 1{,}2 \times 1{,}3 \\ &= \color{#ec0000}{2{,}34 \ \text{dm}^3} \end{align}|| -
Créer une équation en fonction du contexte
Le volume qui est donné s’applique à toute la boite à lunch. Il faut donc additionner le volume de la pyramide et celui du prisme. ||\begin{align} \text{Volume total} &= \text{Somme des volumes de tous les solides} \\ 3{,}65 &= \color{#333fb1}{0{,}6x} + \color{#ec0000}{2{,}34} \end{align}|| -
Résoudre l'équation
||\begin{align} 3{,}65 \color{#ec0000}{-2{,}34} &= {0{,}6x} +{2{,}34} \color{#ec0000}{-2{,}34} \\ \color{#ec0000}{\dfrac {\color{black}{1{,}31}}{0{,}6}}&= \color{#ec0000}{\dfrac {\color{black}{0{,}6x}}{0{,}6}} \\ 2{,}18 &\approx x \end{align}|| -
Interpréter la réponse selon le contexte
La hauteur totale de la boite à lunch est de ||\begin{align}\text{Hauteur totale} &= 1{,}3 + x\\ &= 1{,}3 + 2{,}18\\ &=3{,}48\ \text{dm.}\end{align}||
Pour trouver une mesure manquante à partir du volume dans des solides complexes avec des équations de degré 2, la démarche à suivre est relativement semblable à celle qui implique des équations de degré 1. Par contre, les méthodes de résolution peuvent inclure la factorisation par la méthode produit-somme ou l'utilisation de la formule quadratique.
Afin de donner une forme satisfaisante aux différentes peluches à l'allure de robots, on doit les rembourrer de façon adéquate. Pour ce faire, on utilise un matériau synthétique qui se vend |2 \ $ / \text{dm}^3.| Pour que le prix de vente final de ce produit soit accessible au maximum de gens possible, on veut limiter les couts de rembourrage à |5{,}60 \ $| par peluche.

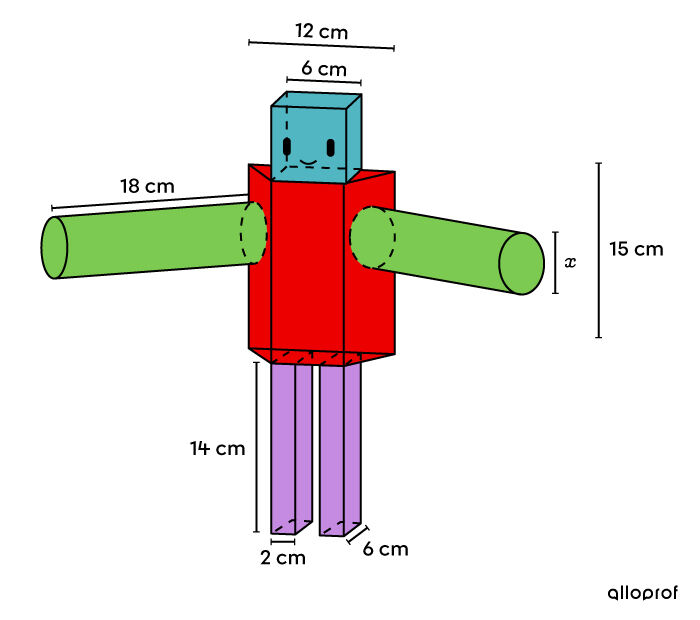
Pour ce modèle, la tête est de forme cubique, le corps est un prisme à base trapézoïdale, les jambes sont des prismes à base rectangulaire et les bras sont des cylindres.
Selon les informations fournies dans le plan de la peluche, quelle devrait être l'épaisseur des bras?
-
Déterminer le volume
||\begin{align} \text{Volume total} &= 5{,}60\ $\div 2\ $/ \text{dm}^3 \\ &= 2{,}80 \ \text{dm}^3\\ &= 2 \ 800 \ \text{cm}^3 \end{align}|| -
Identifier la mesure manquante avec une variable
On cherche l’épaisseur du bras qui correspond au diamètre (ou au double du rayon) du disque formant la base du cylindre. En associant |x| au rayon, cela facilite les calculs de volume.
-
Associer au volume de chaque solide une valeur numérique ou une expression algébrique
||\begin{align} \color{#51b6c2}{V_\text{cube}}&=c^3\\ &= 6^3 \\ &= \color{#51b6c2}{216 \ \text{cm}^3}\\\\ \color{#c58ae1}{V_\text{prisme}}&=A_b \times h\\ &= 6 \times 2 \times 14\\ &= \color{#c58ae1}{168 \ \text{cm}^3}\\\\ \color{#ec0000}{V_\text{prisme}} &= A_b \times h \\ &= \displaystyle \left(\frac{(6+12)\times 6}{2}\right) \times 15 \\ &= \color{#ec0000}{810 \ \text{cm}^3}\\\\ \color{#7cca51}{V_\text{cylindre}} &=A_b \times h \\ &= \pi x^2 \times 18\\ &= \color{#7cca51}{18\pi x^2\ \text{cm}^3} \end{align}|| -
Créer une équation en fonction du contexte
||\begin{align} \text{Volume total} &= \text{Somme des volumes de tous les solides} \\ 2\ 800 &= \color{#51b6c2}{216} + 2 \times \color{#c58ae1}{168}+ \color{#ec0000}{810} + 2 \times \color{#7cca51}{18\pi x^2} \\ 2\ 800 &= \color{#51b6c2}{216} + \color{#c58ae1}{336}+ \color{#ec0000}{810} + \color{#7cca51}{36\pi x^2} \end{align}|| -
Résoudre l'équation
||\begin{align} 2\ 800 &= 1 \ 362 + 36\pi x^2 \\ 2\ 800\color{#ec0000}{-1 \ 362} &= 1 \ 362 \color{#ec0000}{-1 \ 362}+ 36\pi x^2 \\ \color{#ec0000}{\dfrac{\color{black}{1\ 438}}{36\pi } }&= \color{#ec0000}{\dfrac{\color{black}{36\pi x^2}}{36\pi }}\\ \color{#ec0000}{\sqrt{\color{black}{12{,}71}}} &\approx \color{#ec0000}{\sqrt{\color{black}{x^2}}} \\ 3{,}57 &\approx x \end{align}|| -
Interpréter la réponse selon le contexte
L’épaisseur des bras doit être de ||\begin{align} \text{Épaisseur du bras} &=2 \times \text{rayon}\\ &= 2 \times 3{,}57\\ &= 7{,}14\ \text{cm.}\end{align}||
Un solide tronqué est un solide auquel on a enlevé une partie. Ainsi, pour trouver une mesure manquante dans un solide tronqué, il faut tenir compte du solide initial et faire la soustraction appropriée.
Afin d’améliorer son image, une compagnie qui produit du jus d'orange veut changer la forme de son contenant. Par contre, elle tient à ce que le nouveau modèle soit obtenu à partir de l'ancien. Ainsi, la section rouge a été obtenue en tronquant horizontalement la pyramide mauve de l'ancien modèle. Finalement, la hauteur totale de la bouteille demeure la même, soit |21 \ \text{cm}.|
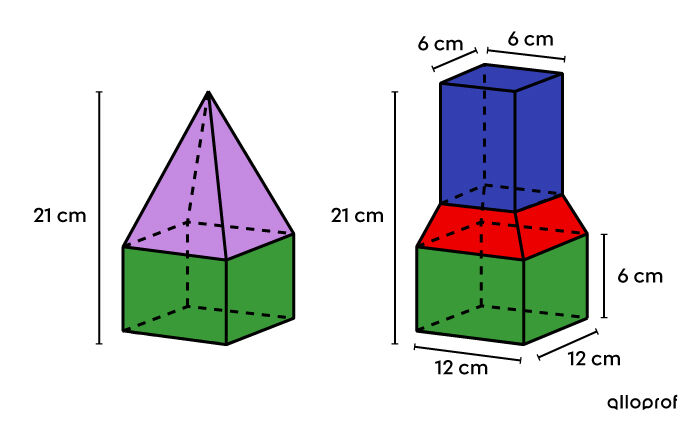
En se fiant aux informations fournies dans le dessin, quelle devrait être la mesure de la hauteur de la partie supérieure du nouveau contenant si on sait que ce modèle a un volume de |1 \ 872 \ \text{cm}^3?|
-
Déterminer le volume
Selon le problème, le volume total du nouveau contenant est de |1 \ 872 \ \text{cm}^3.| -
Identifier la mesure manquante avec une variable
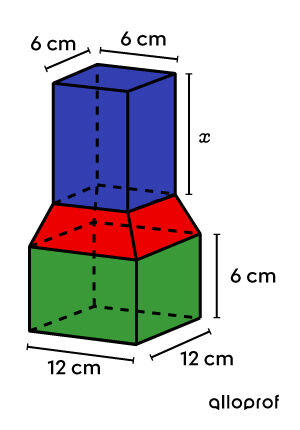
On cherche la hauteur du prisme bleu.
-
Associer au volume de chaque solide une valeur numérique ou une expression algébrique
||\begin{align} \color{#333fb1}{V_\text{prisme}} &= A_b \times h \\ &= 6^2\times x \\ &= \color{#333fb1}{36 x\ \text{cm}^3}\\\\ \color{#3a9a38}{V_\text{prisme}} &= A_b \times h \\ &= 12^2 \times 6 \\ &= \color{#3a9a38}{864\ \text{cm}^3}\\\\ \end{align}|| Il reste à déterminer le volume de la pyramide tronquée. On doit tenir compte de la pyramide initiale.
La hauteur de la pyramide mauve de l’ancien modèle est de ||\begin{align} \text{Hauteur de la pyramide mauve} &= 21 - 6 \\ &= 15\ \text{cm.}\end{align}||
Comme le nouveau modèle a la même hauteur que l’ancien, la hauteur du morceau de pyramide qu’on retire est identique à la hauteur du prisme bleu dans le nouveau modèle.
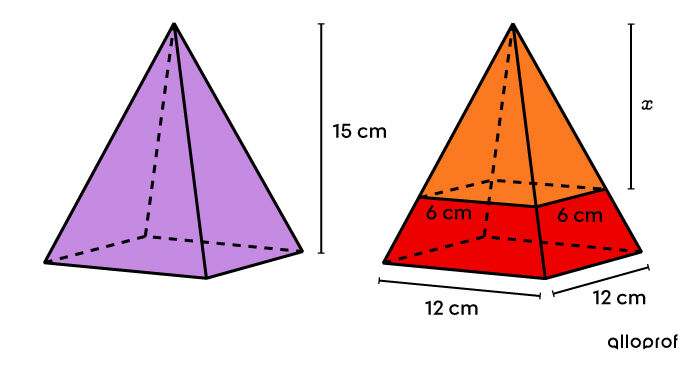
||\begin{align} \color{#ec0000}{V_\text{pyramide tronquée}} &= \color{#c58ae1}{V_\text{pyramide}} - \color{#fa7921}{V_\text{pyramide}} \\ &= \color{#c58ae1}{\dfrac{A_b \times h}{3}}- \color{#fa7921}{\dfrac{A_b \times h}{3}}\\ &= \color{#c58ae1}{\dfrac{12^2 \times 15}{3}} -\color{#fa7921}{\frac{6^2\times x}{3}} \\ &= \color{#ec0000}{720 - 12x} \end{align}||
-
Créer une équation en fonction du contexte
||\begin{align} \text{Volume total} &= \text{Somme des volumes de tous les solides} \\ 1\ 872 &= \color{#333fb1}{36x} + \color{#3a9a38}{864} + \color{#ec0000}{720 - 12x} \\ \end{align}|| -
Résoudre l'équation
||\begin{align} 1\ 872 &= 24x + 1 \ 584 \\ 1\ 872 \color{#ec0000}{-1\ 584}&= 24x + 1 \ 584 \color{#ec0000}{-1\ 584} \\ \color{#ec0000}{\dfrac {\color{black}{288}}{24}}&= \color{#ec0000}{\dfrac {\color{black}{24x}}{24}}\\ 12 &= x \end{align}|| -
Interpréter la réponse selon le contexte
La mesure de la hauteur de la partie supérieure du nouveau contenant est de |12\ \text{cm}.|
Un solide décomposable est un solide qui peut être séparé en plusieurs solides plus simples. Pour trouver une mesure manquante dans un solide décomposable, on procède généralement en le décomposant. Pour ce faire, on identifie les différents solides qui le composent et on soustrait ceux qui sont retirés.
Avec Noël qui approche, un nouveau produit sort sur le marché. En résumé, il s'agit d'une boule neigeuse en verre de forme cubique à l'intérieur de laquelle on a enlevé une partie de forme cylindrique afin d'y insérer la photo d'un être cher.
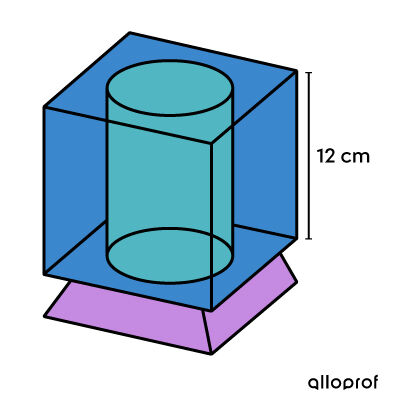
Pour assurer le mouvement des flocons de neige artificiels qui sont dans la section fermée du cube, cette dernière est remplie à |90\ \%| d'un liquide, ce qui représente |1{,}010\ 7\ \text{L}| de liquide. À la lumière de ces informations, détermine le diamètre de la portion cylindrique de ce produit.
-
Déterminer le volume
On peut poser une proportion à l’aide des informations du problème : ||\begin{align} \frac{90}{100} &= \frac{1{,}010 \, 7 \ \text{L}} {? \ \text{L}}\\\\ ?&=\dfrac{100\times 1{,}010 \, 7}{90}\\?&=1{,}123 \ \text{L}\\ ?&=1{,}123\ \text{dm}^3\\?&=1 \ 123 \ \text{cm}^3 \end{align}|| -
Identifier la mesure manquante avec une variable
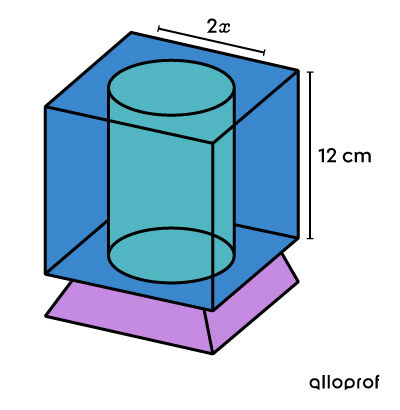
On cherche le diamètre du cylindre. Comme on a besoin du rayon dans les calculs, on choisit |2x| pour représenter le diamètre. Ainsi, |x| est le rayon.
-
Associer au volume de chaque solide une valeur numérique ou une expression algébrique
||\begin{align}\color{#3b87cd}{V_\text{cube}} &= c^3 \\ &= 12^3 \\ &=\color{#3b87cd}{1 \ 728 \ \text{cm}^3} \\\\ \color{#51b6c2}{V_\text{cylindre}} &= A_b \times h \\&= \pi x^2 \times 12\\ &=\color{#51b6c2}{12\pi x^2\ \text{cm}^3} \end{align}|| -
Créer une équation en fonction du contexte
||\begin{align} V_\text{total} &= \color{#3b87cd}{V_\text{cube}} - \color{#51b6c2}{V_\text{cylindre}} \\ 1 \ 123 &= \color{#3b87cd}{1 \ 728} - \color{#51b6c2}{12\pi x^2} \end{align}|| -
Résoudre l'équation
||\begin{align} 1 \ 123 \color{#ec0000}{-1\ 728} &= 1 \ 728\color{#ec0000}{-1\ 728} - 12\pi x^2 \\ \color{#ec0000}{\dfrac{\color{black}{-605}}{-12\pi }} &= \color{#ec0000}{\dfrac{\color{black}{-12\pi x^2}}{-12\pi }} \\ \color{#ec0000}{\sqrt{\color{black}{16{,}05}}} &\approx \color{#ec0000}{\sqrt{\color{black}{x^2}}} \\ 4{,}01 &\approx x \end{align}|| Ainsi, le rayon du cylindre est d’environ |4{,}01\ \text{cm}.| -
Interpréter la réponse selon le contexte
Le diamètre de la section cylindrique de ce produit est de ||\begin{align} \text{Diamètre} &= 2x\\ &= 2 \times 4{,}01 \\ &=8{,}02 \ \text{cm.} \end{align}||
Pour valider ta compréhension de la marche à suivre pour trouver des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante :
