La force gravitationnelle est le phénomène de réaction physique qui cause l'attraction mutuelle entre deux corps.
En général, cette attraction se fait entre un objet et un astre comme la Terre ou la Lune. Cette force produit une accélération gravitationnelle
La Lune tourne autour de la Terre, car elle est attirée par elle.
Lorsqu'une personne saute à la corde à danser, elle retombe au sol, car la Terre exerce une attraction sur cette personne.
Il est important de spécifier que la gravité s’exerce toujours entre deux objets. Si l’objet A attire l’objet B, alors l’objet B attire aussi l’objet A avec la même force. C’est le principe derrière la troisième loi de Newton.
On utilise la formule suivante pour trouver la force gravitationnelle d'une masse.
|F_{g} = m \times g|
où
|F_{g}| représente la force gravitationnelle en Newtons |\small (\text {N})|
|m| représente la masse du corps en kilogrammes |\small (\text {kg})|
|g| représente l'intensité du champ gravitationnel en Newtons par kilogramme |\small (\text {N/kg})|
Quelle est la force gravitationnelle exercée sur une pomme de |\small \text {50 g}| sur la Terre et sur la Lune?
Il est important de convertir la masse en kilogrammes.
|m = 50 \: \text {g} = 0,05 \: \text {kg}|
Pour calculer la force gravitationnelle sur la Terre:
||\begin{align} F_{g} = m \times g \quad \Rightarrow \quad
F_{g} &= 0,05 \: \text {kg} \times 9,8 \: \text {N/kg}\\
&= 0,49 \: \text {N} \end{align}||
Pour calculer la force gravitationnelle sur la Lune:
||\begin{align} F_{g} = m \times g \quad \Rightarrow \quad
F_{g} &= 0,05 \: \text {kg} \times 1,6 \: \text {N/kg}\\
&= 0,08 \: \text {N} \end{align}||
Lorsqu'un corps est en chute libre, il se dirige vers le sol ou, plus précisément, vers le centre de la Terre. Il doit suivre cette trajectoire, car il existe une force d'attraction, la force gravitationnelle, qui amène le corps à se rapprocher du centre de l'autre objet qui l'attire. En absence de résistance de l'air, la chute libre se fera avec une accélération équivalente à l'accélération gravitationnelle terrestre, soit |\small 9,8 \: \text {m/s}^2|.
Le poids d'un objet est la mesure de la force gravitationnelle exercée par la Terre sur un objet.
La force gravitationnelle exercée par un objet est donc égale au poids de cet objet. Ainsi, deux objets ayant une masse identique auront nécessairement le même poids s'ils sont tous deux situés dans un même endroit. Toutefois, si un de ces objets était laissé sur Terre alors que l'autre était amené sur la Lune, le poids varierait, car la force gravitationnelle ne serait plus la même. Toutefois, la masse ne changerait pas, car, par définition, la masse représente la quantité de matière qui constitue un objet.
Quelle est la force gravitationnelle avec laquelle la Terre attire un objet de |\small \text {70 kg}| ? Quelle est la masse et quel est le poids de cet objet sur la Lune?
Pour déterminer la force gravitationnelle sur la Terre:
||\begin{align} F_{g} = m \times g \quad \Rightarrow \quad
F_{g} &= 70 \: \text {kg} \times 9,8 \: \text {N/kg}\\
&= 686 \: \text {N} \end{align}||
La masse de l'objet sur la Lune ne changera pas. Peu importe où cet objet est situé, la quantité de matière sera la même. La masse sur la Lune est donc |\small \text {70 kg}|.
Pour déterminer la force gravitationnelle sur la Lune:
||\begin{align} F_{g} = m \times g \quad \Rightarrow \quad
F_{g} &= 70 \: \text {kg} \times 1,6 \: \text {N/kg}\\
&= 112 \: \text {N} \end{align}||
La loi de la gravitation universelle est une équation qui permet de calculer la force gravitationnelle (|F_{g}|) avec laquelle deux corps s’attirent l’un vers l’autre.
|\displaystyle F_{g} = \frac{G \cdot m_{1} \cdot m_{2}}{r^{2}}|
où
|F_{g}| représente la force d'attraction entre les corps |\small (\text {N})|
|G| représente la constante de la gravitation universelle |\small \left( 6,67 \times 10^{-11} \displaystyle \frac {\text {N} \cdot \text {m}^{2}}{\text {kg}^{2}} \right)|
|m_{1}| représente la masse du premier objet |\small (\text {kg})|
|m_{2}| représente la masse du deuxième objet |\small (\text {kg})|
|r| représente la distance séparant les deux objets |\small (\text {m})|
La planète Terre a une masse d’environ |\small 5,98 \times 10^{24} \: \text {kg}| et tourne à une distance moyenne de |\small 1,50 \times 10^{8} \: \text {km}| du Soleil dont la masse est d’environ |\small 1,99 \times 10^{30} \: \text {kg}|. Quelle est la force qui permet à la Terre de continuer sa révolution autour du Soleil?
Les informations connues dans ce problème sont les suivantes.
||\begin{align}G &= 6,67 \times 10^{-11} \: \frac {\text {N} \cdot \text {m}^{2}}{\text {kg}^{2}} &m_{\text {Terre}} &= 5,98 \times 10^{24} \: \text {kg} \\
m_{\text {Soleil}} &= 1,99\times 10^{30} \: \text {kg} &r_{\text {Terre-Soleil}} &= 1,50 \times 10^{11} \: \text {m}\end{align}||
En utilisant la loi de la gravitation universelle, la force peut être mesurée.
||\begin{align} \displaystyle F_{g} &= \frac{G \cdot m_{\text {Terre}} \cdot m_{\text {Soleil}}}{r^{2}}\\
&= \frac{{6,67 \times 10^{-11} \displaystyle \frac {\text {N} \cdot \text {m}^{2}}{\text {kg}^{2}} \cdot 5,98 \times 10^{24} \space \text {kg} \cdot 1,99 \times 10^{30} \space \text {kg}}}{(1,50 \times 10^{11} \space \text {m})^{2}} \\
&= 3,53 \times 10^{22} \space \text {N} \end{align}||
Un rocher de |\small \text {300 kg}| se trouve à la surface de la Lune dont la masse est de |\small 7,35 \times 10^{22} \: \text {kg}|. Si la Lune a un rayon d’environ |\small 1,74 \times 10^{6} \: \text {m}|, quelle force permet à la roche de demeurer sur la surface de la Lune ?
La difficulté dans ce problème est d’évaluer la distance qui sépare le rocher de la Lune. Il est faux de croire que la distance est nulle, puisqu’il faut utiliser le centre d’une masse (ou le centre de la Lune dans notre cas) comme point de référence pour évaluer les distances. La distance qui sépare cet objet du centre de la Lune sera donc le rayon lunaire.
Les informations connues dans ce problème sont les suivantes.
||\begin{align}G &= 6,67 \times 10^{-11} \: \frac {\text {N} \cdot \text {m}^{2}}{\text {kg}^{2}} &m_{\text {rocher}} &= 300 \: \text {kg}\\
m_{\text {Lune}} &= 7,35 \times 10^{22} \: \text {kg} &r_{\text {rocher-Lune}} &= 1,74\times 10^{6} \: \text {m}\end{align}||
La loi de la gravitation universelle permet de calculer la force exercée entre la Lune et le rocher.
||\begin{align} \displaystyle F_{g} &= \frac{G \cdot m_{\text {Terre}} \cdot m_{\text {Soleil}}}{r^{2}} \\
&= \frac{{6,67 \times 10^{-11} \displaystyle \frac {\text {N} \cdot \text {m}^{2}}{\text {kg}^{2}} \cdot 300 \: \text {kg} \cdot 7,35 \times 10^{22} \: \text {kg}}}{(1,74 \times 10^{6} \: \text {m})^{2}} \\
&= 486 \: \text {N} \end{align}||
Lorsqu'un objet se trouve sur un plan incliné, une partie de la force gravitationnelle se retrouve parallèlement au déplacement d'un objet. Cette force est parfois appelée force de plan ou force en x. Pour trouver cette force, on doit utiliser les formules trigonométriques dans un triangle rectangle.
Quelle est la force gravitationnelle parallèle au déplacement d'une masse de |\small \text {100 kg}| ?
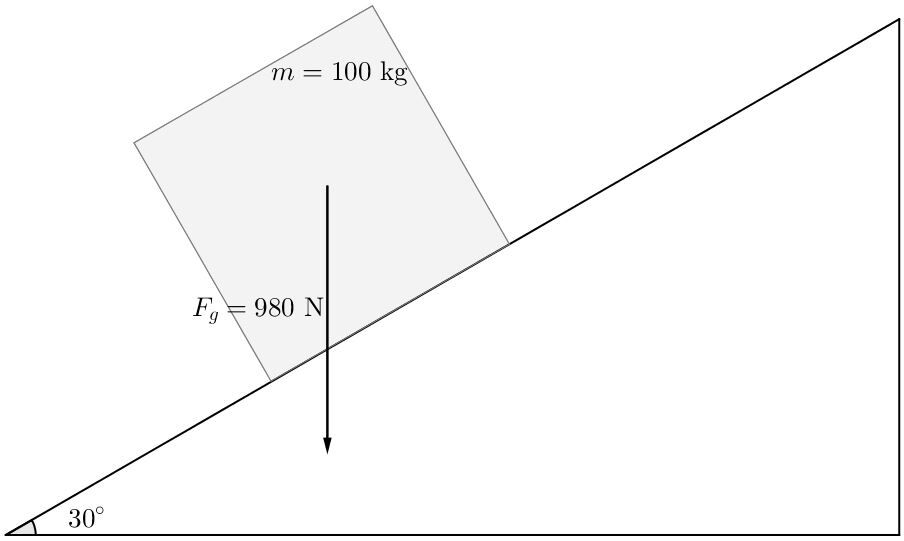
La force gravitationnelle est toujours orientée vers le centre de la Terre (vers le sol). Elle est perpendiculaire à la surface du sol.
La force normale est une force perpendiculaire à la pente dans le plan. Si l'on prolonge la normale vers le bas, l'angle formé entre celle-ci et la force gravitationnelle est le même que l'angle de la pente.
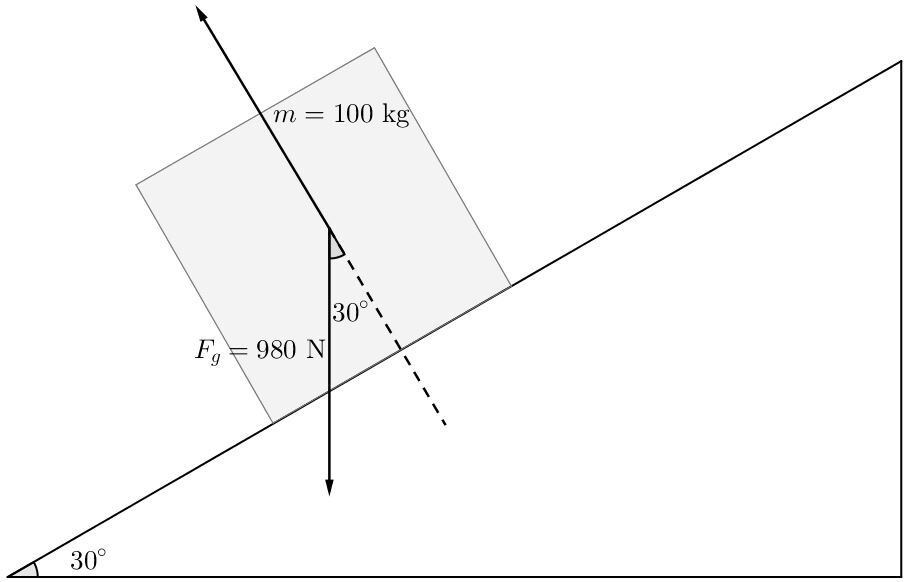
La force gravitationnelle parallèle au déplacement sera la force opposée à l'angle.
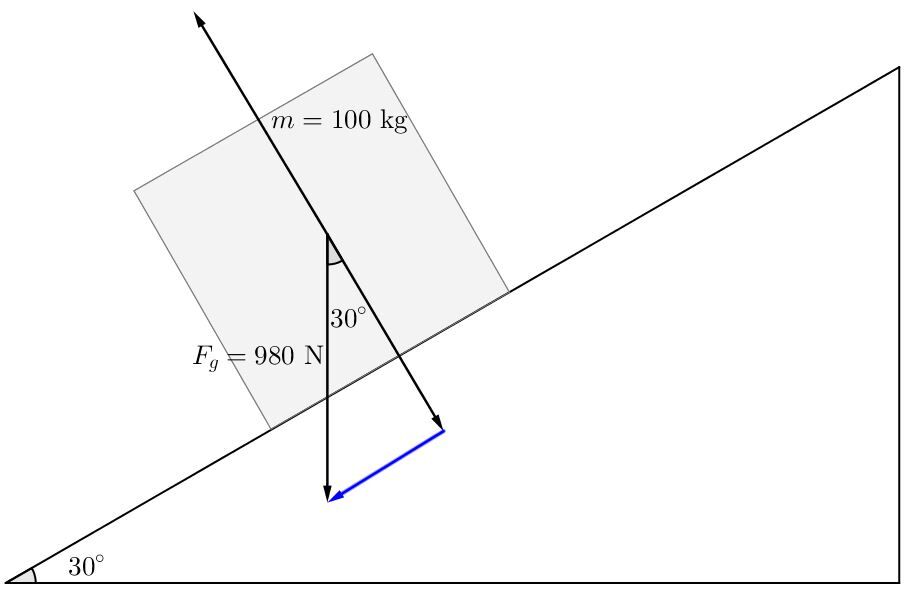
En utilisant les rapports trigonométriques, il est possible de déterminer la valeur de la force parallèle au déplacement.
||\begin{align} \sin \Theta = \frac {\text {F}_\text{x}}{\text {F}_\text{g}}
\quad \Rightarrow \quad
\text {F}_\text{x} &= \sin \Theta \times \text {F}_\text{g} \\
&= \sin \: 30^{\circ} \times 980 \space \text {N}\\
&= 490 \: \text {N} \end{align}||
Isaac Newton (1643-1727) est un physicien britannique reconnu pour avoir établi les trois lois universelles du mouvement en 1688. Ces trois lois, dites lois de Newton, ont permis d'élaborer la base de la mécanique classique.
- La première loi de Newton décrit le principe d'inertie, soit le principe selon lequel un corps conserve son état de mouvement à la condition qu'aucune force extérieure n'agisse sur lui. L'application d'une force modifiera son état de mouvement et lui fera subir une accélération vectorielle (changement de vitesse et/ou d'orientation).
- La deuxième loi de Newton décrit ce qui se passe lorsqu'une force est exercée sur un objet. De plus, elle présente une formule mathématique permettant de calculer l'intensité de cette force.
Pour valider ta compréhension à propos de la deuxième loi de Newton de façon interactive, consulte la MiniRécup suivante :

- La troisième loi de Newton mentionne que si une force est appliquée sur un objet, il existe une force de même grandeur et de même direction mais de sens opposé à la première force.
Dans les fiches suivantes, chacune des lois sera expliquée en détail:


