La loi d’Ohm met en relation la différence de potentiel, la résistance et l’intensité du courant dans un circuit électrique.
|U=RI|
où
|U\ :| différence de potentiel en volts |\text{(V)}|
|R\ :| résistance en ohms |(\Omega)|
|I\ :| intensité du courant en ampères |\text{(A)}|
À partir de la formule précédente, on peut établir les 3 relations suivantes.
-
Si |R| est constante et que |I| augmente, alors |U| augmente.
-
Si |I| est constante et que |R| augmente, alors |U| augmente.
-
Si |U| est constante et que |R| augmente, alors |I| diminue.
Voici un graphique de la différence de potentiel en fonction de l’intensité du courant.
Déplace les curseurs pour faire varier l’intensité du courant ou la résistance.
Dans le graphique précédent, on remarque que :
-
Lorsque l’intensité du courant augmente, la différence de potentiel augmente proportionnellement.
-
Le taux de variation (pente) correspond à la résistance.
-
Plus la résistance est élevée, plus la pente est abrupte.
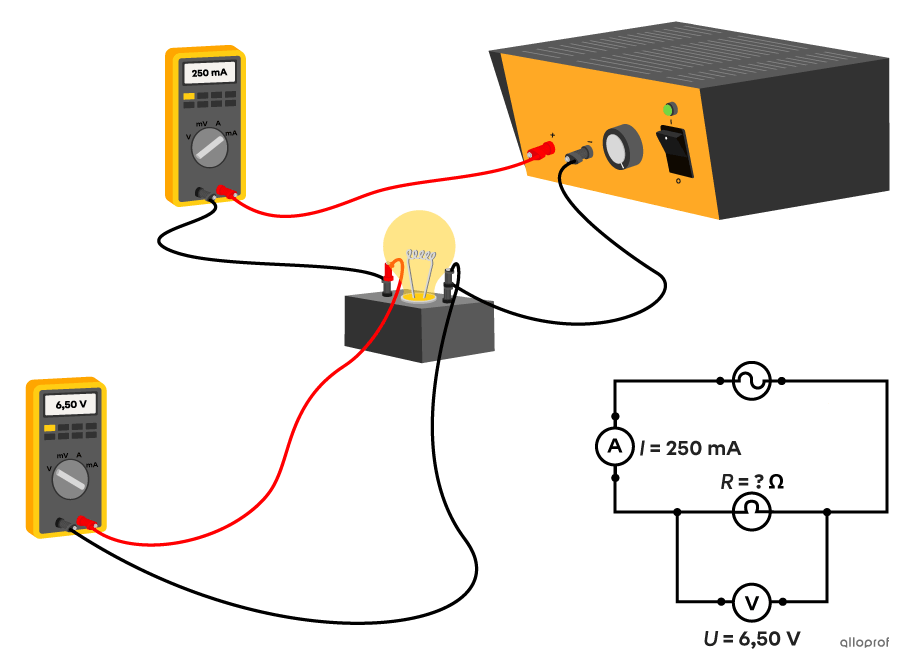
En laboratoire, on a un circuit électrique comprenant une source de courant et une ampoule.
On ajoute un ampèremètre branché en série et un voltmètre branché en parallèle aux bornes de l’ampoule.
L'ampèremètre mesure un courant électrique de |250\ \text{mA}.| Le voltmètre mesure une différence de potentiel de |6{,}50\ \text{V}.|
Quelle est la résistance de l’ampoule?
- On identifie les données.
||\begin{align} I&=250\ \cancel{\text{mA}}\times\ \dfrac{1\ \text{A}}{1\ 000\ \cancel{\text{mA}}}&=0{,}250\ \text{A}\\U&=6{,}50\ \text{V}\\R&=\text{?}\ \Omega\end{align}|| - On choisit la formule et on isole |R.|
||\begin{align}U&=R\ \times \ I\\\\\dfrac{U}{I}&=\dfrac{R\ \times \ \cancel{I}}{\cancel{I}}\\\\\dfrac{U}{I}&=R\end {align}|| - On remplace les données dans la formule et on fait le calcul.
||\begin{align}R&=\dfrac{6{,}50\ \text{V}}{0{,}250\ \text{A}}\\\\R&=26{,}0\ \Omega \end{align}|| - On répond à la question.
La résistance de l’ampoule est de |26{,}0\ \Omega.|
Le circuit d'un jouet télécommandé a une résistance de |120\ \Omega.| S’il est conçu pour un courant de |0{,}05\ \text{A},| quelle différence de potentiel la pile du jouet doit-elle fournir?
-
On identifie les données.
||\begin{align} R&=120\ \Omega\\I&=0{,}05\ \text{A}\\U&=\text{?}\ \text{V} \end{align}|| -
On choisit la formule.
||U=R\times I|| -
On remplace les données dans la formule et on fait le calcul.
||\begin{align}U&=120\ \Omega\times0{,}05\ \text{A}\\U&=6{,}00\ \text{V}\end{align}|| -
On répond à la question.
La pile doit fournir une différence de potentiel de |6{,}00\ \text{V}| au circuit pour permettre au jouet télécommandé de fonctionner.
Un téléphone portable utilise une batterie de |3{,}7\ \text{V}.| Si la résistance du circuit interne est de |18{,}5\ \Omega,| quelle est l’intensité du courant en milliampères |(\text{mA})| qui traverse le circuit?
-
On identifie les données.
||\begin{align} U&=3{,}7\ \text{V}\\R&=18{,}5\ \Omega\\I&=\text{?}\ \text{mA} \end{align}|| -
On choisit la formule et on isole |I.|
||\begin{align}U&=R\times I\\\dfrac{U}{R}&=\dfrac{\cancel{R}\times I}{\cancel{R}}\\\\\dfrac{U}{R}&=I\end{align}|| -
On remplace les données dans la formule et on fait le calcul.
||\begin{align}I&=\dfrac{3{,}7\ \text{V}}{18{,}5\ \Omega}\\\\I&=0{,}20\ \text{A}\end{align}|| -
On convertit les |\text{A}| en |\text{mA}.|
||I=0{,}20\ \cancel{\text{A}}\times\dfrac{1\ 000\ \text{mA}}{1\ \cancel{\text{A}}}=200\ \text{mA}|| -
On répond à la question.
L’intensité du courant qui parcours le circuit du téléphone portable est de |200\ \text{mA}| ou |2{,}0 \times \ 10^{2}\ \text{mA}.|
Pour valider ta compréhension à propos de l'électricité de façon interactive, consulte la MiniRécup suivante :

Pour valider ta compréhension à propos des calculs dans les circuits électriques de façon interactive, consulte la MiniRécup suivante :
