-
Le travail est un transfert d’énergie lié au déplacement d’un objet.
-
La force efficace est la composante d'une force responsable du déplacement d'un objet.
-
Le déplacement est la distance qui sépare le point de départ du point d’arrivée d'un objet.
Le travail effectué sur un objet varie en fonction du déplacement de cet objet et de la force efficace appliquée sur celui-ci :
-
plus le déplacement est grand, plus le travail effectué sur cet objet est grand;
-
plus la force efficace est grande, plus le travail effectué sur l’objet est grand.
Par convention, l’unité de mesure du travail est le joule (|\text{J}|) : 1 joule est la quantité d’énergie nécessaire pour déplacer un objet sur une distance de 1 mètre (|\text{m}|) à l’aide d’une force efficace de 1 newton (|\text{N}|).
La relation mathématique suivante permet de calculer le travail exercé sur un objet.
|W = F_{eff} \cdot \Delta s|
où
|W| représente le travail (|\text{J}|)
|F_{eff}| représente la force efficace (|\text{N}|)
|\Delta s| représente le déplacement de l'objet (|\text{m}|)
La force efficace est la composante de la force appliquée qui est parallèle au déplacement d’un objet. La force efficace a la même orientation que le déplacement.
Elle peut aussi être identifiée comme « la force parallèle au déplacement ».
Une grue soulève une poutre sur une distance de |20\ \text {m}| en hauteur. Pour ce faire, la grue applique une tension constante de |1\ 000\ \text {N}| vers le haut.
Quel est le travail effectué par la grue pour déplacer la poutre?

La force appliquée et le déplacement de la poutre sont parallèles (vers le haut). Le travail peut se calculer de la manière suivante.
D’abord, on identifie les données.
|\begin{align} &W=?\ \text{J} &F_{eff}= 1\ 000\ \text{N} &\\ &\Delta s= 20\ \text{m} \end{align}|
Ensuite, on identifie la formule à utiliser et on remplace les données.
|\begin{align} W&=F_{eff}\cdot \Delta s\\ W&= 1\ 000\ \text{N} \times 20 \ \text{m}\\ W&=20\ 000\ \text{J}\end{align}|
La grue effectue un travail de |20\ 000\ \text{J}| (|20\ \text{kJ}|) sur la poutre.
Une personne applique horizontalement une force de |100\ \text{N}| sur un charriot chargé de disques de fonte. Malgré tout, le charriot reste immobile.
Quelle est la quantité de travail effectuée par la personne sur le charriot?
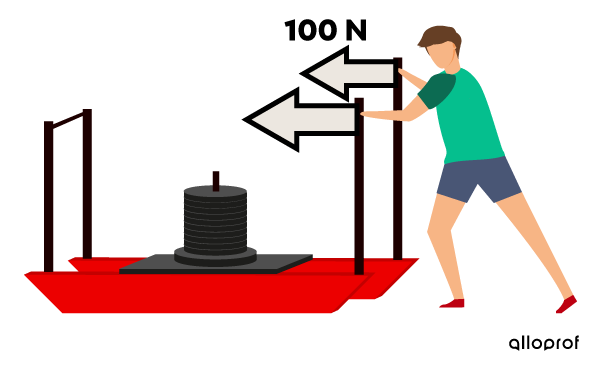
Puisque le travail correspond à l'énergie fournie pour déplacer un objet et que le charriot ne subit aucun déplacement, le travail sera nul.
Voici la démarche.
D’abord, on identifie les données.
|\begin{align} &W=?\ \text{J} &F_{eff}= 100\ \text{N} &\\ &\Delta s= 0\ \text{m} \end{align}|
Ensuite, on identifie la formule et on remplace les données.
|\begin{align} W&=F_{eff}\cdot \Delta s\\ W&= 100\ \text{N} \times 0 \ \text{m}\\ W&=0\ \text{J}\end{align}|
La personne effectue un travail de |0\ \text {J}| sur le charriot.
Le calcul du travail est obtenu par produit scalaire, soit la multiplication de deux vecteurs. Il s’agit alors d'un vecteur de force et d'un vecteur de déplacement.
De plus, lorsque la force appliquée sur un objet n’est pas parallèle au déplacement, il faut déterminer la force efficace par un rapport trigonométrique dans un triangle rectangle avant de calculer le travail.
Une personne tire une boite sur une distance de |5\ \text{m}| en appliquant une force de |40\ \text {N}| selon un angle de |30^\circ| par rapport à l’horizontale.
Quel est le travail effectué par la personne sur la boite?

Puisque la force appliquée n’est pas parallèle au déplacement de la boite, il faut d’abord déterminer la force efficace à l’aide d’un rapport trigonométrique.
-
Trace un triangle rectangle dont l'hypoténuse correspond à la force appliquée sur la boite (|40\ \text{N}|). Le côté adjacent à l’angle de |30^\circ| représente la force efficace (en rouge sur le schéma).

-
Détermine la grandeur de la force efficace.
D’abord, on identifie les données. Ensuite, on identifie la formule à utiliser et on remplace les données.
|\begin{align} &\theta=30^\circ\\ &\text{hypothénuse (force appliquée)}=40\ \text{N}\\ &\text{côté adjacent (force efficace)}=?\ \text{N} \end{align}| |\begin{align}cos\ \theta&=\frac{\text{coté adjacent}}{\text{hypoténuse}}\\ cos\ 30^{\circ}&=\frac{\color{red}{F_{eff}}}{40\ \text{N}}\\ \color{red}{F_{eff}}&=cos\ 30^{\circ}\times 40\ \text{N}\\\color{red}{F_{eff}}&\approx 34{,}6\ \text{N}\end{align}|
La force efficace est d'environ |34{,}6\ \text{N}|.
-
On peut maintenant calculer le travail.
D’abord, on identifie les données. Ensuite, on identifie la formule à utiliser et on remplace les données.
|\begin{align}&W=?\ \text{J} &F_{eff}=34{,}6\ \text{N}\\&\Delta s=5\ \text{m}\end{align}|
|\begin{align}W&=F_{eff}\cdot\Delta s\\W&=34{,}6\ \text{N} \times 5\ \text{m}\\W&=173\ \text{J}\end{align}|
Un travail de |\text {173 J}| est effectué sur la boite.
Lorsqu'on effectue un travail, on utilise de l'énergie. Selon la loi de la conservation de l'énergie, l'énergie n'est ni perdue ni créée : elle est transférée ou transformée. Ainsi, le travail reçu par un corps est équivalent à sa variation d’énergie.
La relation mathématique entre le travail et la variation d'énergie est la suivante :
|W=\Delta E|
où
|W| représente le travail |\text {(J)}|
|\Delta E| représente la variation d'énergie (cinétique ou potentielle) |\text {(J)}|
Une personne applique une force suffisante pour mettre en mouvement un panier d’épicerie à une vitesse de |1{,}5\ \text {m/s}|.
Le panier et son contenu ont une masse totale de |15\ \text{kg}|.
Quel est le travail effectué par la personne pour amener le panier à une vitesse de |1{,}5\ \text{m/s}|?

Lorsque le panier se met en mouvement, il acquiert une énergie cinétique, qui dépend de sa masse et de sa vitesse. La variation d’énergie du panier |\Delta E| est donc équivalente à l’énergie cinétique acquise lorsqu’il atteint sa vitesse finale (|E_{k_{\text{finale}}}|).
||\Delta E=E_{k_{\text{finale}}}||
Il suffit de trouver l’énergie cinétique du panier d’épicerie. Elle est équivalente au travail exercé sur le panier.
D’abord, on identifie les données. Ensuite, on identifie la formule à utiliser et on remplace les données.
|\begin{align}
&E_{k_{\text{finale}}}=?\ \text{J}\\
&m=15\ \text{kg}\\
&v=1{,}5\ \text{m/s}
\end{align}|
|\begin{align} E_{k_{\text{finale}}} &= \dfrac {1}{2} m v^{2} \\ E_{k_{\text{finale}}}&= \dfrac {1}{2} \times 15\ \text {kg} \times \text {(1,5 m/s)}^{2} \\ E_{k_{\text{finale}}}&\approx 16{,}9\ \text {J} \\ \end{align}|
Finalement, le travail est équivalent à la variation d’énergie cinétique.
||\begin{align}
W &=\Delta E \\
W &\approx 16{,}9\ \text {J}
\end{align}||
Le travail fourni par la personne est environ de |16{,}9\ \text {J}.|