Avogadro’s law is a simple gas law.
Avogadro’s law describes the relationship between the volume |(V)| and the quantity of gas expressed in moles |(n)|.
At constant pressure and temperature, when the quantity of gas increases, the volume it occupies increases.
Conversely, when the quantity of gas decreases, the volume decreases.
Move the slider up and down to change the number of moles in the syringe.
At constant pressure and temperature, particles maintain the same degree of agitation and the same average distance between them. Under these conditions, a larger number of particles necessarily takes up more space than a smaller number of particles.
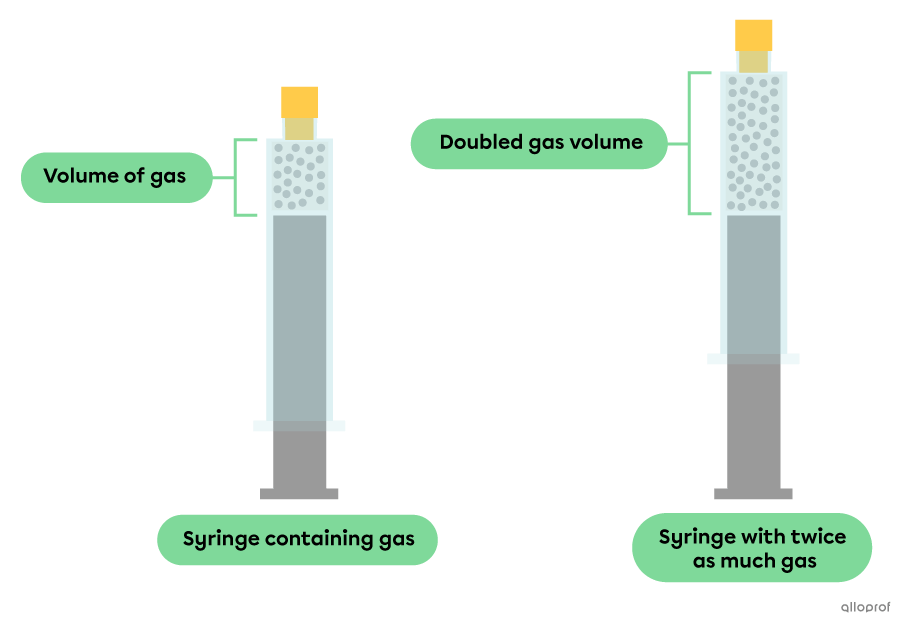
The volume of a gas is directly proportional to its number of moles. This relationship can be expressed using the following formula.
When |P| and |T| are constant:
|V\propto n| or |\dfrac{V}{n}=\text{constante}|
where
|V :| volume often in litres |(\text{L})|
|n :| quantity of gas in moles |(\text{mol})|
We can also compare an initial situation with a final situation in which the volume and number of moles of a gas have changed by using the following formula.
When |P| and |T| are constant:
|\dfrac{V_1}{n_1} = \dfrac{V_2}{n_2}|
where
|V_1:| initial volume often in litres |(\text{L})|
|n_1:| initial quantity of gas in moles |(\text{mol})|
|V_2:| final volume often in litres |(\text{L})|
|n_2:| final quantity of gas in moles |(\text{mol})|
This mathematical relationship is linked to Avogadro's hypothesis, which makes it possible to determine the molar volume of a gas |(V_m),| i.e. the volume occupied by one mole of any gas under specific temperature and pressure conditions.
Simple gas laws only apply to ideal gases.
In other words, the values calculated using simple gas laws correspond approximately to the real values, as long as the gas temperature is not too low and its pressure not too high.
The version of Avogadro's law presented here is modernized. At the time of chemist and physicist Amedeo Avogadro, the concept of moles was not yet well defined in the scientific community. In the 18th century, the term equivalent mass (or equivalent weight) was used and it was at the end of the 19th century that the term mole came into use.
So how did Avogadro formulate the law that bears his name?
When his work was published in 1811, Avogadro's law was formulated as a hypothesis which stated that, at the same temperature and pressure, two equal volumes of different gases have the same number of molecules[1].

Source: Sergio Delle Vedove, Shutterstock
Thanks to this hypothesis and by evaluating the mass of gas, Avogadro was able to determine what we now call the molar mass of different compounds. This was revolutionary! Keep in mind that determining the molar mass of a compound was no easy matter at the time, since the periodic table and the measurement instruments we have today did not yet exist.
A rubber balloon with a volume of |6{.}00\ \text{L}| contains |3{.}50\ \text{mol}| of helium. The maximum volume of the balloon is |14{.}9 \ \text{L}.| How many moles of helium can be added to the balloon? Assume that the pressure and temperature remain constant.
-
Identify the given values.
|\begin{align}
V_1 &= 6{.}00\ \text{L}\\
n_1 &= 3{.}50\ \text{mol}\\
V_2 &= 14{.}9 \ \text{L}\\
n_2 &= ?
\end{align}|
|P| and |T| are constant.
-
Choose the formula. Because |P| and |T| are constant, Avogadro’s law can be applied.
|\dfrac{V_1}{n_1} = \dfrac{V_2}{n_2}|
-
Isolate |V_2| and plug the given values in the formula.
|\begin{align}
n_2 &=\dfrac{V_2\times n_1}{V_1}\\
n_2 &=\dfrac{14{.}9\ \text{L}\times 3{.}50\ \text{mol}}{6{.}00\ \text{L}}\\
n_2 &\approx 8{.}70\ \text{mol}
\end{align}|
-
The final number of moles is subtracted from the initial number of moles to determine the amount of gas that can be added to the balloon.
|\begin{align}
\Delta n &= n_2 - n_1\\
\Delta n &= 8{.}70\ \text{mol} - 3{.}50\ \text{mol}\\
\Delta n &= 5{.}20\ \text{mol}
\end{align}|
The maximum amount of helium that can be added to the balloon is |5{.}20{mole}.|
Video coming soon
Exercise coming soon.
- Avogadro, A. (1810). Essai d’une manière de déterminer les masses relatives des molécules élémentaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons. Journal de Physique, de chimie et d’histoire naturelle. 73: 58–76.