The area of a cylinder’s base is calculated using the formula for the area of the circle that defines it. The formula to calculate the area of this plane figure is as follows.
||A_b = \pi r^2|| where ||\begin{align}A_b&: \text{Area of a base}\\r&: \text{radius}\end{align}||
Depending on the context, either one or both of the cylinder’s bases may be considered.
To warn other drivers to keep their distance, a trucker who transports cylindrical tree trunks paints the end of the trunks red when they stick out past the rest of the load.
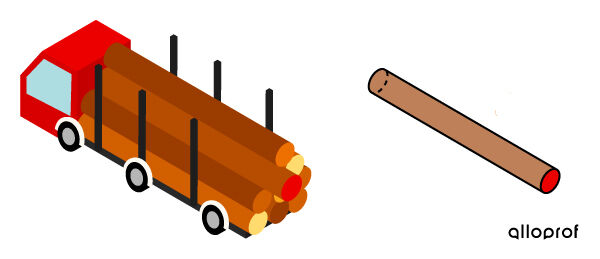
What is the measure of the painted surface if the trunks have an average radius of |15\ \text{cm}?|
-
Identify the relevant faces
Only the measure of one of the bases is sought. Thus, the calculation required is the area of a single circle. -
Apply the formula ||\begin{align} A_b &= \pi r^2\\ &= \pi (15)^2\\ &\approx 706.86\ \text{cm}^2\end{align}||
-
Interpret the answer
The painted surface has an area of approximately |706.86\ \text{cm}^2.|
In a different situation, we may need to find the area of both bases. We would use the same approach, making sure to multiply the area of the base by |2| when interpreting the answer.
Based on the net of a cylinder, it is possible to deduce that the lateral face is actually a rectangle that wraps around the circumference of each circular base.
This wrapping can be represented as follows.

This image shows that: ||\begin{align} \color{#3A9A38}{\text{Lateral side base}} &= \color{#3A9A38}{\text{Circumference of the circle}}\\
\color{#51B6C2}{\text{Lateral side height}} &= \color{#51B6C2}{\text{Cylinder height}}\\\\
\Rightarrow\ \text{Lateral side area} &= \color{#3A9A38}{\text{Circumference}}\times \color{#51B6C2}{\text{Height}}\end{align}||
Taking this information into account, the following area formula can be determined.
||A_L = 2 \pi r h|| where ||\begin{align} A_L:\text{lateral Area}\\r:\text{radius of the base} \\ h: \text{cylinder height} \end{align}||
Use the process below to put it all into practice.
To properly display the manufacturer's trademark on its highlighters, a sales manager decides to place a sticker on the entire lateral surface of the markers.
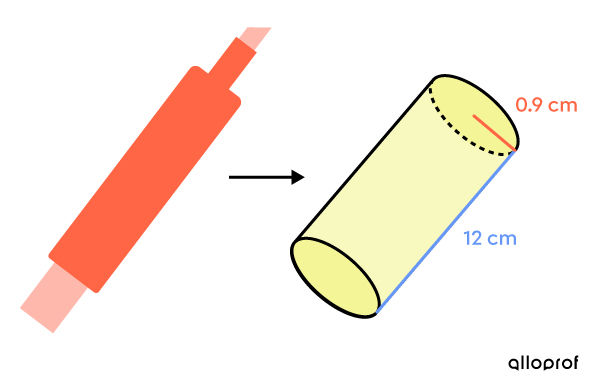
Determine the area of the sticker using this information.
-
Identify the solid
The highlighter is cylindrical. In this problem, the lateral area of the cylinder must be calculated. -
Apply the formula ||\begin{align} A_L &= 2 \pi r h\\ &= 2 \pi (0{.}9) \times 12\\ &\approx 67.86 \ \text{cm}^2\end{align}||
-
Interpret the answer
The sticker’s area is approximately |67.86 \ \text{cm}^2.|
To find the total area of a solid, add the area of its bases and its lateral area (as is done for prisms).
||A_T = 2A_b + A_L|| where ||A_T:\text{total Area}||
Again, this formula may change depending on the situation. For example, only one of the two bases may be required.
An innovative company that manufactures water bottles lets its customers print the designs they want on every surface of the bottles.

According to this model, what is the measurement of the surface upon which the customers can print designs?
-
Identify the relevant faces
In this situation, all of the cylinder’s faces must be considered. -
Calculate the area of a base ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{0.85}{2}\right)^2\\ &\approx 0.57\ \text{dm}^2\end{align}||
-
Calculate the lateral area ||\begin{align} A_L &= 2 \pi r h\\ &= 2 \pi \left(\dfrac{0.85}{2}\right) \times 2.3\\ &= 0.85\pi \times 2.3\\&\approx 6.14\ \text{dm}^2\end{align}||
-
Calculate the total area ||\begin{align}A_T &= 2 A_b + A_L\\ &= 2 (0.57) + 6.14\\ &= 7.28\ \text{dm}^2\end{align}||
-
Interpret the answer
The surface upon which it is possible to print patterns is |7.28 \ \text{dm}^2.|
Sometimes, the total area is given and only one of the measures of the base or the height of the cylinder is sought. This is called finding a missing measurement of a cylinder from the area. In this case, the approach is a little different, but it is still important to remember the formula for the total area of a cylinder.
| Area of a Base | ||A_b = \pi r^2|| | ||\begin{align}A_b&: \text{Area of a base}\\r&: \text{radius}\end{align}|| |
|---|---|---|
| Lateral Area | ||A_L = 2 \pi r h|| | ||\begin{align} A_L:\text{lateral Area}\\r:\text{radius of the base} \\ h: \text{cylinder height} \end{align}|| |
| Total Area | ||A_T = 2A_b + A_L|| | ||A_T:\text{total Area}|| |