Since cones are solids with curved surfaces, the formulas used to calculate their area and volume are different from those used for pyramids. When looking at a cone’s net, notice how the base is formed by a circle and the lateral face is formed by a sector of a circle.
A cone’s base is formed by a circle. The formula for calculating the area of this circle is as follows.
||A_b = \pi r^2|| where ||\begin{align}A_b&:\text{Area of the base}\\r &: \text{radius}\end{align}||
Apply this formula to determine the area of the base when the measure of the radius is known.
To ensure that a parking space is well lit, determine the area of the ground that is covered by the light from the lamppost.
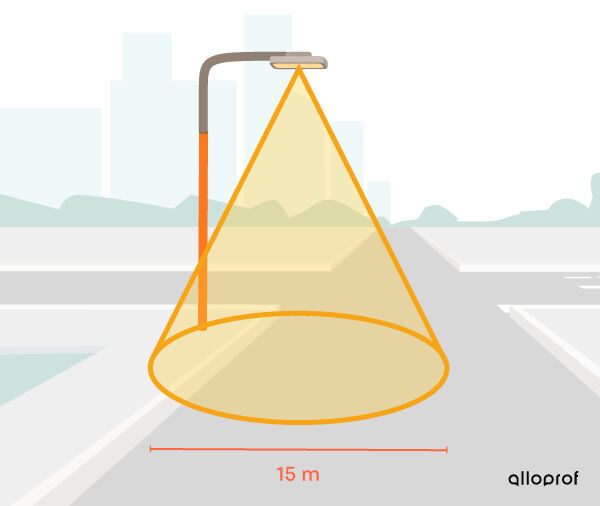
-
Identify the relevant faces
In this case, as with all right circular cones, the base is a circle. -
Apply the formula ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{15}{2}\right)^2\\ &= 56.25\pi \\ &\approx 176.71 \ \text{m}^2\end{align}||
-
Interpret the answer
The surface illuminated by the lamppost has an area of approximately |176.71 \ \text{m}^2.|
Even if the formula may seem simple to apply, it is important to use the right measurements. Here, the |15\ \text{m}| refers to diameter, not radius. Divide this measure by |2| to get the desired measurement.
Because of its unique net, the lateral area of a cone may seem difficult to summarise in a single formula. However, the various properties of the latter allow us to deduce the formula below.
||A_L = \pi r a|| where ||\begin{align} A_L&:\text{lateral Area}\\r &: \text{radius of the base}\\ a &: \text{apothem of the cone}\end{align}||
A representation of a cone is used to estimate the amount of fabric needed to make a dress.
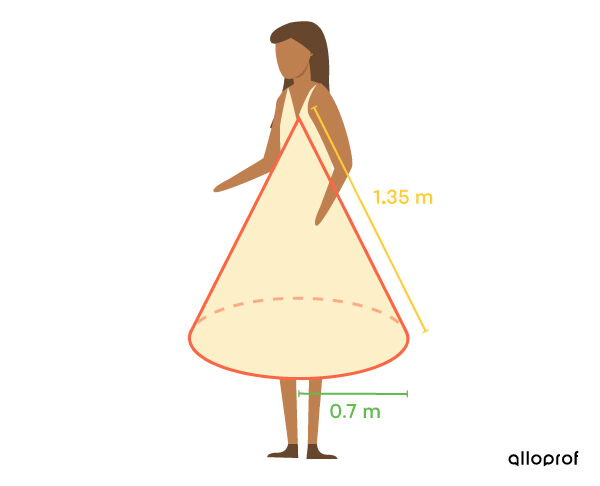
Given that this dress is made with silk, which costs |$12\ /\text{m}^2,| how much will it cost to purchase enough fabric?
-
Identify the solid
This conical dress is not closed at the bottom, so it is only necessary to calculate the lateral area. -
Apply the formula ||\begin{align} A_L &= \pi r a\\ &= \pi (0.7) (1.35)\\ &= 0.945\pi \\ &\approx 2.97 \ \text{m}^2\end{align}||
-
Interpret the answer
Since it costs |$12 / \text{m}^2,| multiply: ||2.97\ \text{m}^2 \times $12\ /\text{m}^2 = $35.64\ || Thus, the fabric can be purchased for |\$35.64.|
Keep in mind that when curved surfaces are put into context, the examples often represent an estimate, and not an exact quantity.
Construct the net of a cone to identify its different defining sides.
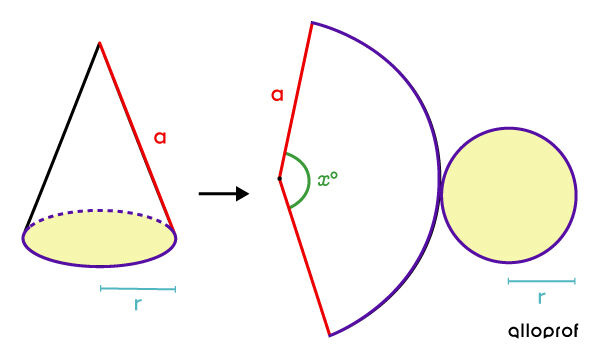
This way, the different links can be observed with the properties of the circle, the central angles, and the sectors of a circle.
Here, the cone’s lateral area is actually the area of the sector of a circle created with the radius |\color{#EC0000}{a}.| It can be represented using the following proportion. ||\begin{align} \dfrac{\text{Area of sector}}{\text{Area of circle}} &= \dfrac{\color{#3A9A38}{\text{Central angle}}}{360^\circ} \\\\\dfrac{\text{Area of sector}}{\pi \color{#EC0000}{a}^2} &= \dfrac{\color{#3A9A38}{x^\circ}}{360^\circ}\\\\ \Rightarrow\ \text{Area of sector} &= \dfrac{\pi \color{#EC0000}{a}^2 \color{#3A9A38}{x}}{360}\end{align}||
The measure of the central angle can also be expressed according to the circle’s arc that it defines. Based on its construction, this circle’s arc corresponds to the circumference of the base, which makes it possible to deduce that:
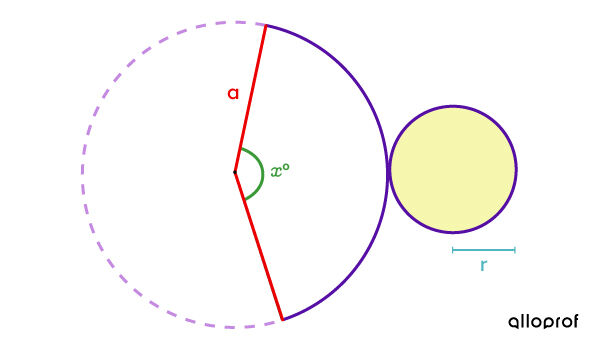
||\begin{align} \dfrac{\color{#3A9A38}{\text{Central angle}}}{360^\circ} &= \dfrac{\color{#560FA5}{\text{Circle arc}}}{\color{#C58AE1}{\text{Circumference}}} \\\\ \dfrac{\color{#3A9A38}{x}^\circ}{360^\circ} &= \dfrac{\color{#560FA5}{\text{Circle arc}}}{\color{#C58AE1}{\text{Circumference}}} \\\\ \dfrac{\color{#3A9A38}{x}^\circ}{360^\circ} &= \dfrac{2 \pi \color{#51B6C2}{r}}{2 \pi \color{#EC0000}{a}}\\\\ \Rightarrow\ \color{#3A9A38}{x} &= \dfrac{360 \times 2 \pi \color{#51B6C2}{r}}{2 \pi \color{#EC0000}{a}} \\\\ \color{#3A9A38}{x} &= \dfrac{360 \color{#51B6C2}{r}}{\color{#EC0000}{a}}\end{align}||
When substituting the algebraic expression associated with |\color{#3A9A38}{x},| we obtain: ||\begin{align} \text{Area of sector}&= \dfrac{\pi \color{#EC0000}{a}^2 \color{#3A9A38}{x}}{360^\circ}\\\\ &= \dfrac{\pi \color{#EC0000}{a}^2 \left(\dfrac{360 \color{#51B6C2}{r}}{\color{#EC0000}{a}}\right)}{360}\\\\ &= \dfrac{360\pi \color{#51B6C2}{r} \color{#EC0000}{a}}{360}\\\\ &= \pi \color{#51B6C2}{r} \color{#EC0000}{a}\end{align}|| Since the area of the sector is the lateral area: ||A_L = \pi \color{#51B6C2}{r} \color{#EC0000}{a}||
Whenever it is a question of total area, consider all the faces of the solid and add their respective surface areas.
||A_T = A_L + A_b|| where ||A_T:\text{total Area}||
Since there is only one figure that serves as the base in a cone, the area of the base is only considered once.
In early 1973, the now-legendary rock band Kiss entered the music industry. To stand out from other bands, the group members decided to dress in a unique way. Among other things, one member decided to integrate conical spikes into his costume.
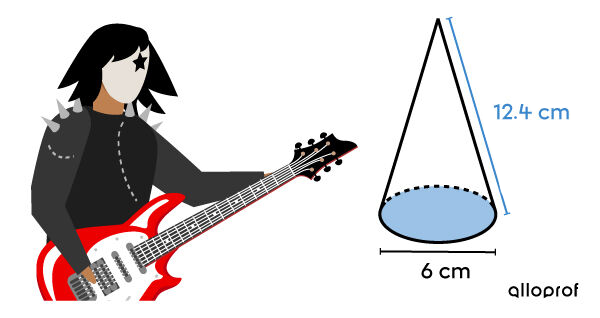
The band member must determine the total area of each spike in order to have them made. Determine the total area using the measurements provided.
-
Identify the relevant faces
All faces of the cone are needed. -
Calculate the area of the base ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{6}{2}\right)^2\\ &= 9\pi \\ &\approx 28.27 \ \text{cm}^2\end{align}||
-
Calculate the lateral area ||\begin{align} A_L &= \pi r a\\ &= \pi \left(\dfrac{6}{2}\right)(12.4)\\ &= 37.2\pi \\ &\approx 116.87 \ \text{cm}^2\end{align}||
-
Calculate the total area ||\begin{align} A_T &= A_L + A_b\\ &= 37.2\pi + 9\pi\\ &= 46.2\pi \\ &\approx 145.14 \ \text{cm}^2\end{align}||
-
Interpret the answer
The total area of each spike on his costume is approximately |145.14 \ \text{cm}^2.|
In other situations, the measure of a dimension of the base or even the cone’s apothem must be found from a given total area. This is called finding a missing measurement of a cone from the area. In this case, the approach is a little different, but it is essential to remember the formula for the total area of the cones.
Despite the numerous formulas, it is possible that some data is missing. If so, use other mathematical concepts to obtain the desired result. For example, the measurement of the apothem is not always given. In those cases, the Pythagorean Theorem is often used to find the result.
In the case of a right cone, it is possible to obtain a right triangle by tracing the cone’s apothem, its height, and the radius of its base.

Since it is a right cone, the height intersects the base’s centre perpendicularly. Thus, the measure of the leg corresponds to the radius of the base.
By associating the measure of a leg with that of the radius of the base, the measure of the other leg with the cone’s height, and the measure of the apothem with that of the hypotenuse, there is enough information to use the Pythagorean Theorem. ||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2&= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{4}^2 + \color{#EC0000}{12}^2 &= \color{#51B6C2}{a}^2\\ 160 &= \color{#51B6C2}{a}^2 \\12.65 \ \text{cm} &\approx \color{#51B6C2}{a} \end{align}|| The apothem of the cone measures approximately |12.65\ \text{cm}.|
When using several concepts simultaneously, be careful not to mix up the variables. On the cone, |\color{#51B6C2}{a}| refers to the apothem, whereas in the Pythagorean Theorem the variable |\color{#51B6C2}{c}| refers to this measurement. As illustrated in the previous example, it helps to use colours when associating numbers with the measurements they represent.
The Pythagorean Theorem must be used when looking for the measurement of the height from the apothem.