Unlike other solids, the area of a sphere cannot be found by dividing it into different parts, such as the lateral area or area of the base. In fact, the lateral area and the total area represent the same surface since there is no base.
Although a sphere is entirely composed of a single curved surface, it is possible to calculate its area.
||A_T = 4 \pi r^2|| where ||r = \text{radius}||
Due to its curved surface, the formula for calculating the area of a sphere and the formula to find the area of a circle bear some resemblance. In both cases, only the radius measurement is necessary to apply the formula.
To ensure that all the baseballs used in the Major League are the same, they are all covered with the same material.
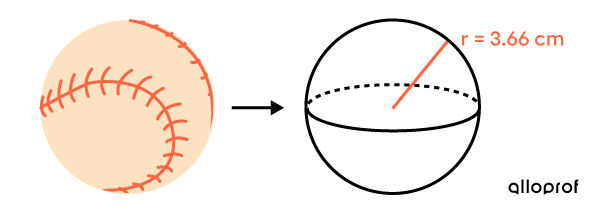
Based on the information given, how many |\text{cm}^2| of material will be used to cover each ball?
-
Identify the solid
Since the area is sought, use the concept of a sphere. -
Apply the formula
||\begin{align} A_T &= 4 \pi r^2 \\ &= 4 \pi (3{.}66)^2\\ &\approx 168{.}33 \ \text{cm}^2 \end{align}|| -
Interpret the answer
The total area of the sphere is approximately |168{.}33 \ \text{cm}^2.|
Even if only one measurement is necessary to complete the calculations, remember that the radius of a sphere is the measurement of the line segment connecting the sphere’s centre to any point on its exterior outline. Thus, the radius does not have to be perfectly horizontal or vertical. Also, other dimensions can be associated with the radius measurement.
Dimensions in a sphere
The radius of the sphere can be associated with its width or height.
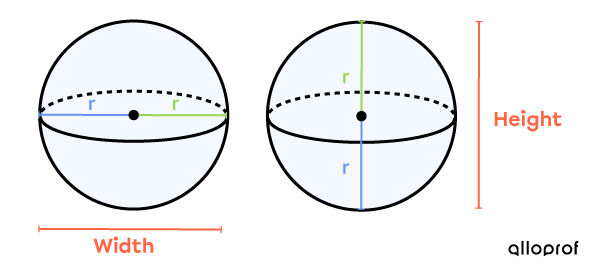
In both cases, |\text{Width} = 2 r = \text{Height}.| This also corresponds to the sphere’s diameter.
Another type of solid with slightly different properties is obtained by dividing the sphere into two equal parts.
Sometimes, when calculating the area of a half-sphere, no new surface appears when the sphere is cut in half. This is an open sphere. In such a case, calculate the area of the complete sphere and divide the result by 2. The context determines whether it is an open or closed half-sphere.
A coating is applied to the interior of a clay bowl during production to make sure the clay isn’t affected by food. How much coating is needed for the bowl below, assuming the bowl is a perfect half-sphere?
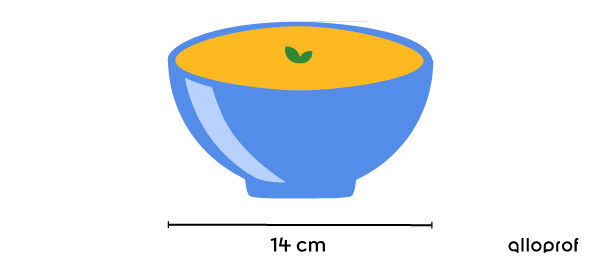
-
Identify the solid
Since the bowl’s interior area is sought, we must find the area of an open half-sphere with a diameter of |14\ \text{cm}.| Therefore, the radius of the bowl is |7\ \text{cm}.| -
Apply the formula
The total area of the sphere is calculated as follows. ||\begin{align} A_T &= 4 \pi r^2\\ &= 4 \pi (7)^2\\&=196\pi\\ &\approx 615{.}75 \ \text{cm}^2\end{align}||
Thus, the area of the half-sphere is |\dfrac{615{.}75}{2} \approx 307{.}88\ \text{cm}^2.| -
Interpret the answer
The interior surface is approximately |307{.}88 \ \text{cm}^2.|
A closed half-sphere is a sphere where half of it is preserved and the opening is covered by a circle.The area of this solid can be determined by adding the area of the half-sphere and the area of a circle.
To obtain the total area of a closed half-sphere, add the area of the circle to half of the sphere’s surface area.
||A_T = 2 \pi r^2 + \pi r^2||
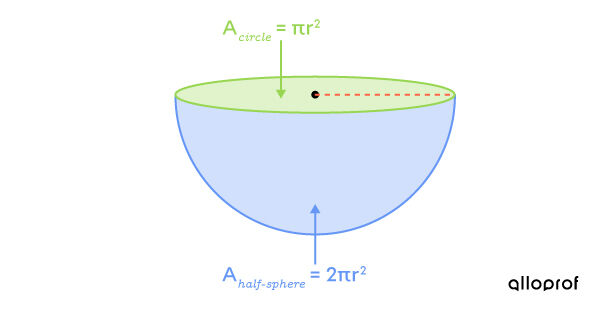
Pay careful attention to the order of the operations when applying the formula.
A coating of nichrome (nickel and chromium alloy) is used to ensure uniform heat distribution in a kettle shaped like a half-sphere.
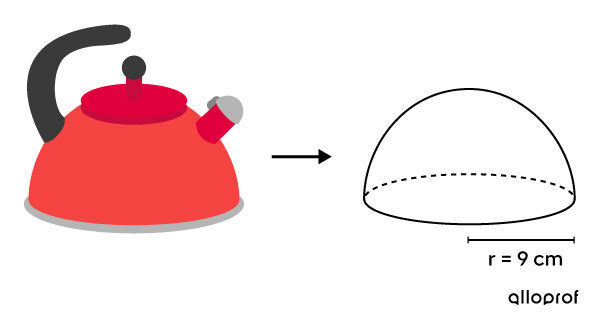
What will be the total cost of the treatment if it costs |$0{.}09\ | to cover a |1\ \text{cm}^2| area with nichrome?
-
Identify the solid
Since it is a kettle, the part that contains the water is a closed half-sphere. -
Apply the formula ||\begin{align} A_T &= 2 \pi r^2 + \pi r^2 \\ &= 2 \pi (9)^2 + \pi (9)^2 \\ &=162\pi + 81\pi \\ &=243\pi \\ &\approx 763{.}41 \ \text{cm}^2 \end{align}||
-
Interpret the answer
Since the area is in |\text{cm}^2,| simply multiply it by the cost in |\text{cm}^2.| ||763{.}41\ \text{cm}^2 \times 0{.}09\ $/\text{cm}^2 \approx $68{.}71||
It will cost |$68{.}71\ | to cover the kettle.
Sometimes, the measurement of the radius or the diameter of a sphere is sought when the surface area is given. This is called finding a missing measurement of a sphere from its area. In this case, the approach is a little different, but it is still necessary to remember the formula for finding the surface area of spheres.