To calculate the probability of an event in a random experiment, we must count all the outcomes in the sample space.
For a simple random experiment, we simply fully list the sample space and count the number of elements it contains.
We roll a die with |12| sides. The sample space is represented by the following set |\Omega|:
||\Omega=\{1,2,3,4,5,6,7,8,9,10,11,12\}||
There are |12| elements in |\Omega,| which means that there are |12| possible outcomes in this random experiment.
In the case of a random multi-step experiment, we must first check if the experiment takes the order into account or not.
If it is a random experiment that takes the order into account, we can use the multiplication rule. This method consists of multiplying the number of choices at each step of the experiment to find the total number of possible outcomes.
We flip a coin, and then draw a marble from a bag that contains |3| red marbles, |2| blue marbles, and |4| green marbles. Since this is a multi-step random experiment where the order is taken into account, we can use the multiplication rule to find the number of possible outcomes.
The 1st step has |2| possibilities (heads or tails) and the 2nd step has |3| (red marble, blue marble, or green marble).
||2\times3=6||
This random experiment has |6| possible outcomes.
The number of possible outcomes of a multi-step random experiment can be calculated using permutations, arrangements and combinations.
There are several modes of representation that allow you to enumerate the possible outcomes.
We can organize the possible outcomes of a 2-step random experiment using a table.
The number of possible outcomes is the total number of boxes in the chart. To find this number, simply multiply the number of rows by the number of columns.
We spin |2| roulette wheels. The numbers |1| to |4| represent different sections of the 1st roulette wheel, while the letters |X,| |Y,| and |Z| represent the sections of the 2nd roulette wheel.
How many possible outcomes are there in this random experiment?
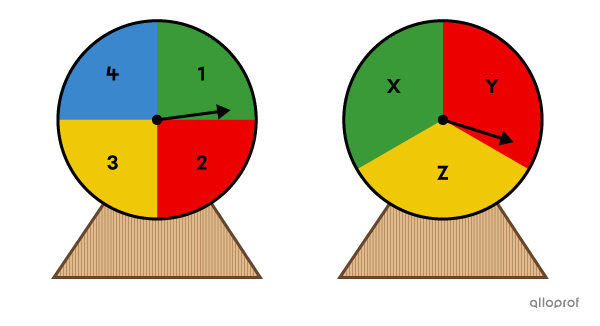
This situation is a multi-step random experiment, since there are |2| steps. The possible outcomes of the 1st roulette wheel are recorded in the 1st column of the table and those of the 2nd roulette wheel in the 1st row of the table. Next, we write the possible outcomes in each box.
| |X| | |Y| | |Z| | |
|---|---|---|---|
| |1| | |(1,X)| | |(1,Y)| | |(1,Z)| |
| |2| | |(2,X)| | |(2,Y)| | |(2,Z)| |
| |3| | |(3,X)| | |(3,Y)| | |(3,Z)| |
| |4| | |(4,X)| | |(4,Y)| | |(4,Z)| |
To enumerate the possible outcomes, simply multiply the number of rows by the number of columns.
||4\times3=12||
Answer: There are |12| possible outcomes in this random experiment.
We can organize the possible outcomes of a multi-step random experiment using a graph or network.
The number of possible outcomes is the total number of pathways one can follow in the network. To find this number, simply multiply the number of branches at each step.
Paul is getting ready to go outside in the spring. He randomly chooses clothing from this category list to wear.
- Toque or a cap
- Coat, raincoat or wool sweater
- Boots, shoes or sandals
How many possible outcomes are there in this random experiment?
This situation is a compound random experiment, since it has |3| steps. We write the possibilities for each step (category) in the network.

To count the possible outcomes, simply multiply the number of branches at each step.
||2\times3\times3=18||
Answer: There are |18| possible outcomes in this random experiment.
We can organize the possible outcomes of a multi-step random experiment using a diagram.
The number of possible outcomes is the total number of connections in the diagram. To find this number, simply add all the connections while being careful not to count the same one twice.
A group of |5| students participate in an arm-wrestling competition. Each student has to compete once against every other student and whoever wins the most games wins the prize.
How many matches are there in this arm wrestling competition?
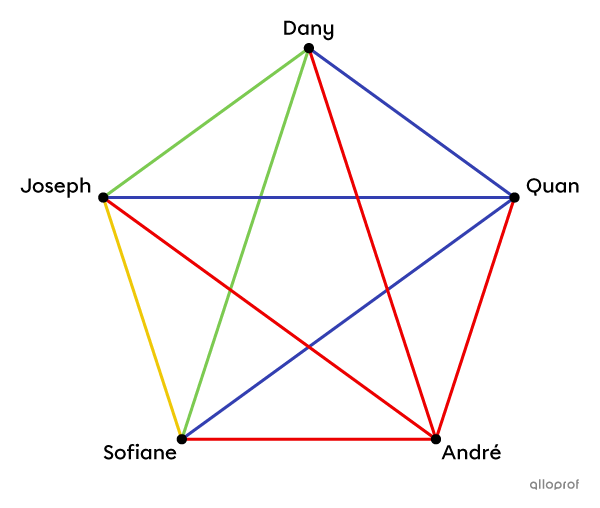
To count the possible outcomes, simply add the number of connections in the diagram. You can use a colour system to avoid counting the same connection twice. André competes against Quan, Dany, Joseph and Sofiane. Then, Quan faces the other 3 opponents, but we do not count his match with André a second time. By applying this same reasoning to the rest of the competitors, we get the total number of possible outcomes as follows.
||\boldsymbol{\color{#ec0000}{4}}+\boldsymbol{\color{#333fb1}{3}}+\boldsymbol{\color{#7cca51}{2}}+\boldsymbol{\color{#efc807}{1}}=10||
Answer: There are |10| possible outcomes in this random experiment.
We can organize the possible outcomes of a multi-step random experiment using a mapping diagram.
The number of possible outcomes is the total number of arrows in the diagram. To find this number, simply count the arrows or multiply the number of elements at each step.
We want to find the number of possible outcomes when we draw a marble from a bag that contains 3 different coloured marbles (green, orange, purple) and then flip a coin.
How many possible outcomes are there in this random experiment?
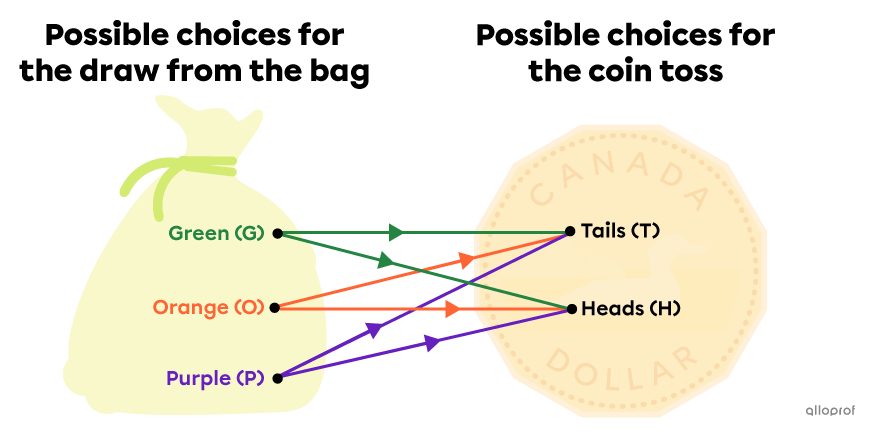
To count the total number of possible outcomes, we can multiply the number of elements of the 1st step |(3)| by the number of elements of the 2nd step |(2).|
||3\times2=6||
Answer: There are |6| possible outcomes in this random experiment.