When trying to calculate a probability in a multi-step random experiment, it is necessary to enumerate the possible outcomes.
To do so, it must first be determined whether order matters or not and if the experiment is with or without replacement. It must also be verified if all of the elements of the starting set are taken into account, or only some. Once this has been done, we can then choose the appropriate method from the following options:
Sequence of all elements of a set where order matters
Sequence of some elements of a set where order matters
Sequence of some elements of a set where order does not matter
Consider the starting set |\{A,B,C\}.|
The permutations of the starting set are as follows:
||\begin{aligned}&(A,B,C)&&(A,C,B)\\&(B,A,C)&&(B,C,A)\\&(C,A,B)&&(C,B,A)\end{aligned}||
Arrangements of 2 out of the 3 elements of the starting set are as follows:
With replacement||\begin{aligned}&(A,A)&&(A,B)&&(A,C)\\&(B,A)&&(B,B)&&(B,C)\\&(C,A)&&(C,B)&&(C,C)\end{aligned}||
Without replacement||\begin{aligned}&&&(A,B)&&(A,C)\\&(B,A)&&&&(B,C)\\&(C,A)&&(C,B)&&\end{aligned}||
Combinations of 2 out the 3 elements of the starting set are as follows:
With replacement||\begin{aligned}&(A,A)&&(A,B)&&(A,C)\\&&&(B,B)&&(B,C)\\&&&&&(C,C)\end{aligned}||
Without replacement||\begin{aligned}&&&(A,B)&&(A,C)\\&&&&&(B,C)\\&&&&&\end{aligned}||
The tree diagram is a good visual representation that helps us to understand the logic behind each of these concepts.
The permutations of a set of elements correspond to the ordered sequences of all the elements of this set.
The permutations of a set are characterized by the order of the elements that form them. For example, |(C,A,B)| and |(B,A,C)| are 2 permutations different than |\{A,B,C\}.|
In other words, the permutations of a random experiment's starting set correspond to the whole sample space of possible outcomes if the experiment has the following characteristics.
-
Order matters in the experiment.
-
The experiment is without replacement.
-
The experiment involves all of the elements of the starting set.
In this case, the permutations are calculated as follows.
||\text{Number of permutations}=n\times(n-1)\times\ldots\times2\times 1||
where
|n:| number of elements in the starting set
We randomly draw all the marbles in a bag without replacement, taking into account the order of the marbles. The bag contains one red marble |(R),| one blue marble |(B),| one yellow marble |(Y)| and one green marble |(G).| How many possible outcomes exist?
We can list the elements of the sample space |(\Omega),| and then count all the elements in this set. However, we notice that this random experiment has the following 3 characteristics:
-
Order matters in this experiment.
-
The experiment is without replacement.
-
The experiment involves all of the elements of the starting set.
It is most efficient to calculate the number of possible outcomes using the formula for the number of permutations of the starting set |\{R,B,Y,G\}.| Since this set contains |4| elements |(n=4),| we calculate the following:
||\begin{align}\text{Number of permutations}&=n\times(n-1)\times\ldots\times2\times 1\\&=4\times3\times2\times1\\&=24\end{align}||
Answer: There are |24| possible outcomes in this random experiment.
The sample space of the previous example can be represented using a tree diagram.
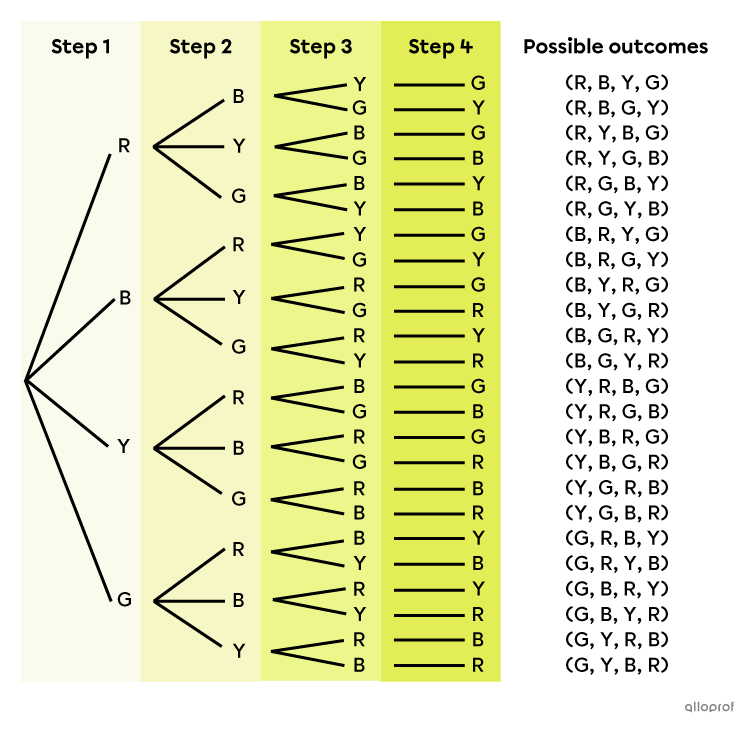
Analyzing this diagram, we notice that there are 4 branches in the 1st step, 3 branches in the 2nd step, 2 branches in the 3rd step and 1 branch in the 4th step. The number of branches decreases by 1 at each step, because we do not replace a marble in the bag after drawing it. Also, since we draw all the marbles in the bag, the number of branches decreases until there is only one choice left.
This is why, according to the multiplication rule, we obtain the formula presented above.
The formula for the number of permutations can be simplified using factorial notation.
||\text{Number of permutations}=n!||
where
|n:| number of elements in the starting set
Therefore, in the previous example, the calculation would have been as follows:
||\begin{align}\text{Number of permutations}&=n!\\&=4!\\&=4\times3\times2\times1\\&=24\end{align}||
Arrangements of a set of elements correspond to the ordered sequences of some of the elements of this set.
The arrangements of a set are characterized by the order of the elements that form them. For example, |(A,C)| and |(C,A)| are 2 different arrangements of the set |\{A,B,C\}.|
In other words, the arrangements of the starting set of a random experiment correspond to the whole sample space of possible outcomes if this experiment has the following characteristics:
-
Order matters in the experiment.
-
The experiment is with replacement or without replacement.
-
The experiment involves some of the elements of the starting set.
In this case, the arrangements are calculated as follows:
With replacement||\begin{gather}\text{Number of arrangements}\\\text{with replacement}\end{gather}=n^k||
Without replacement||\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}=n\times(n-1)\times\ldots\times(n-k+1)||
where
|n:| number of elements in the starting set
|k:| number of selected elements in the starting set
Here is an example of a random experiment with replacement:
We randomly draw 2 marbles from a bag with replacement, taking into account the order of the marbles. The bag contains one red marble |(R),| one blue marble |(B),| one yellow marble |(Y)| and one green marble |(G).| How many possible outcomes exist?
We can list the elements of the sample space |(\Omega),| and then count all the elements in this set. However, we notice that this random experiment has the following 3 characteristics:
-
Order matters in this experiment.
-
The experiment is with replacement.
-
The experiment involves some of the elements of the starting set.
It is more efficient to calculate the number of possible outcomes using the formula for the number of arrangements with replacement of the starting set |\{R,B,Y,G\}.| Since this set contains |4| elements |(n=4),| and we choose |2| of these |(k=2),| we calculate the following:
||\begin{aligned}\begin{gather}\text{Number of arrangements}\\\text{with replacement}\end{gather}&=n^k\\&=4^2\\&=16\end{aligned}||
Answer: There are |16| possible outcomes in this random experiment.
We can represent the sample space of the previous example using a tree diagram.
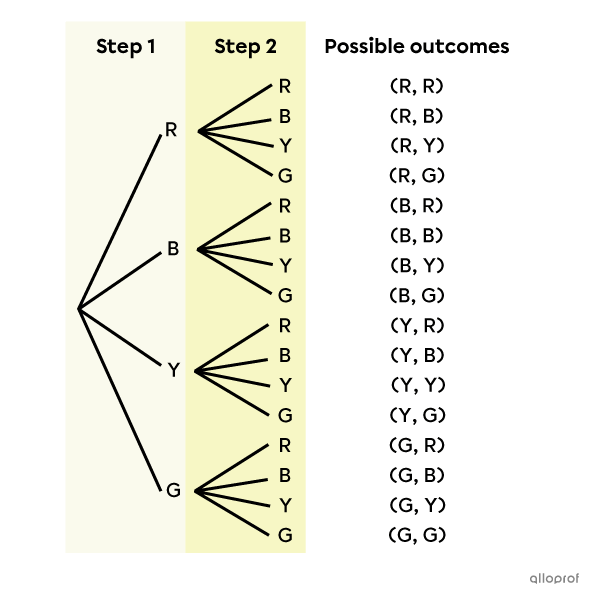
Analyzing this diagram, we notice that there are 4 branches in the first step and 4 branches in the second step. The number of branches does not decrease at each step, because we always replace the marble in the bag after drawing it.
This is why, according to the multiplication rule and exponential notation, we obtain the formula presented above.
||\begin{aligned}\begin{gather}\text{Number of arrangements}\\\text{with replacement}\end{gather}&=\underbrace{4\times 4}_{2\ \text{times}}\\&=\underbrace{n\times n}_{k\ \text{times}}\\&=n^k\end{aligned}||
Here is an example of a random experiment without replacement:
We randomly draw 2 marbles from a bag with replacement, taking into account the order of the marbles. The bag contains one red marble |(R),| one blue marble |(B),| one yellow marble |(Y)| and one green marble |(G).| How many possible outcomes exist?
We can list the sample space |(\Omega),| and then count all the elements in this set. However, we notice that this random experiment has the following 3 characteristics:
-
Order matters in this experiment.
-
The experiment is without replacement.
-
The experiment involves some of the elements of the starting set.
It is most efficient to calculate the number of possible outcomes using the formula for the number of arrangements without replacement of the starting set |\{R,B,Y,G\}.| Since this set contains |4| elements |(n=4),| and we choose |2| of these |(k=2),| we calculate the following, starting with |4| and ending with |n-k+1=4-2+1=3.|
||\begin{aligned}\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}&=n\times(n-1)\times\ldots\times(n-k+1)\\&=4\times3\\&=12\end{aligned}||
Answer: There are |12| possible outcomes in this random experiment.
We can represent the sample space of the previous example using a tree diagram.
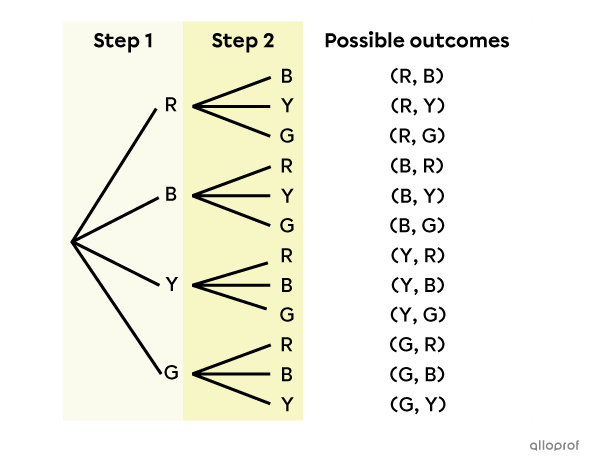
Analyzing this diagram, we notice that there are 4 branches in the 1st step and 3 branches in the 2nd step. The number of branches decreases by 1 at each step, because we never replace the marble in the bag after drawing it. Also, since we do not draw all the marbles in the bag, the number of branches decreases until we have completed all the steps of the experiment.
This is why, according to the multiplication rule, we obtain the formula presented above.
The formula for the number of arrangements without replacement can be simplified using factorial notation.
||\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}=\dfrac{n!}{(n-k)!}||
where
|n:| number of elements in the starting set
|k:| number of selected elements in the starting set
Therefore, in the previous example, we could have performed the following calculation.
||\begin{aligned}\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}&=\dfrac{n!}{(n-k)!}\\&=\dfrac{4!}{(4-2)!}\\&=\dfrac{4!}{2!}\\&=\dfrac{4\times3\times2\times1}{2\times1}\\&=12\end{aligned}||
The combinations of a set of elements correspond to the ordered sequences of some of the elements of this set.
The combinations of a set are not characterized by the order of the elements that form them. For example, |(A,C)| and |(C,A)| are 2 equivalent combinations of the set |\{A,B,C\}.|
In other words, the combinations of the starting set of a random experiment correspond to the whole sample space of possible outcomes if this experiment has the following characteristics:
-
Order doesn’t matter in the experiment.
-
The experiment is with replacement or without replacement.
-
The experiment involves some of the elements of the starting set.
When the experiment is without replacement, we calculate the combinations as follows:
||\begin{gather}\text{Number of combinations}\\\text{without replacement}\end{gather}=\dfrac{\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}}{\begin{gather}\text{Number of permutations}\\\text{of the arrangements}\end{gather}}||
The concept of combinations involves permutations and arrangements. However, the permutations of the arrangements must be calculated, not the permutations of the starting set.
In other words, to calculate the permutations of the arrangements, we must use the formula for permutations which uses the value of |k| rather than the value of |n.|
||\begin{gather}\text{Number of permutations}\\\text{ of the arrangements}\end{gather}=k\times(k-1)\times\ldots\times2\times1||
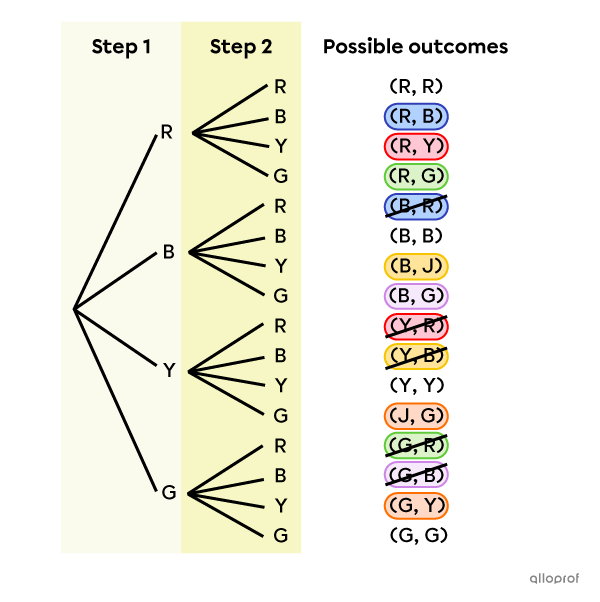
We randomly draw 2 marbles from a bag without replacement and without taking into account the order of the marbles. The bag contains one red marble |(R),| one blue marble |(B),| one yellow marble |(Y)| and one green marble |(G).| How many possible outcomes exist?
We could enumerate the universe of possibilities |(\Omega),| eliminate the results that are equivalent, then count the remaining elements in this set. However, notice that this random experiment has the 3 characteristics below.
-
Order does not matter in this experiment.
-
The experiment is without replacement.
-
The experiment involves some of the elements of the starting set.
It is therefore more efficient to calculate the number of possible outcomes using the formula for the number of combinations without replacement.
||\begin{gather}\text{Number of combinations}\\\text{without replacement}\end{gather}=\dfrac{\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}}{\begin{gather}\text{Number of permutations}\\\text{of the arrangements}\end{gather}}||
Since the starting set |\{R,B,Y,G\}| contains |4| elements |(n=4)| and we choose |2| of them |(k=2),| we calculate the following.
We start by calculating the number of arrangements without replacement by stopping the multiplication at |n-k+1=4-2+1=3.|
||\begin{aligned}\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}&=n\times(n-1)\times\ldots\times(n-k+1)\\&=4\times3\\&=12\end{aligned}||
Then, we calculate the number of permutations of the arrangements. Be careful! Here, we use the value of |2| and not |4.| Since we are interested in the permutations of the arrangements and not in the permutations of the starting set, we must use the value of |k| rather than the value of |n.|
||\begin{aligned}\begin{gather}\text{Number of permutations}\\\text{of the arrangements}\end{gather}&=k\times(k-1)\times\ldots\times2\times1\\&=2\times1\\&=2\end{aligned}||
Lastly, we replace these 2 values in the formula of the number of combinations without replacement.
||\begin{aligned}\begin{gather}\text{Number of combinations}\\\text{without replacement}\end{gather}&=\dfrac{\begin{gather}\text{Number of arrangements}\\\text{without replacement}\end{gather}}{\begin{gather}\text{Number of permutations}\\\text{of the arrangements}\end{gather}}\\&=\dfrac{12}{2}\\&=6\end{aligned}||
Answer: There are |6| possible outcomes in this random experiment.
We can represent the sample space of the previous example using a tree diagram.
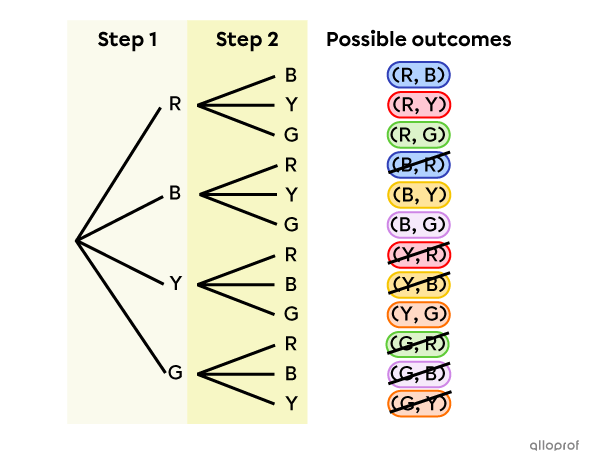
Analyzing this diagram, we notice that there are 4 branches in the 1st step and 3 branches in the 2nd step. The number of branches decreases by 1 at each step, because we do not replace the marble in the bag after drawing it. Also, since we do not draw all the marbles in the bag, the number of branches decreases until we have completed all the steps of the experiment. Also, by observing the 12 results at the end of the branches, we notice that there are equivalent groupings of 2.
This is why we must divide the number of arrangements |(12)| by their number of permutations |(2),| as in the formula presented above.
The formula for the number of combinations without replacement can be simplified using factorial notation.
||\begin{gather}\text{Number of combinations}\\\text{without replacement}\end{gather}=\dfrac{n!}{k!(n-k)!}||
where
|n:| number of elements in the starting set
|k:| number of selected elements in the starting set
Therefore, in the previous example, we could have performed the following calculation.
||\begin{aligned}\begin{gather}\text{Number of combinations}\\\text{without replacement}\end{gather}&=\dfrac{n!}{k!(n-k)!}\\&=\dfrac{4!}{2!(4-2)!}\\&=\dfrac{4!}{2!\times2!}\\&=\dfrac{4\times3\times2\times1}{2\times1\times2\times1}\\&=6\end{aligned}||
In a multi-step random experiment where the order does not matter, the number of combinations of some of the elements of the starting set is calculated as follows:
||\begin{gather}\text{Number of combinations}\\\text{with replacement}\end{gather}=\dfrac{(n+k-1)!}{k!(n-1)!}||
where
|n:| number of elements in the starting set
|k:| number of selected elements in the starting set
We randomly draw 2 marbles from a bag with replacement and without taking into account the order of the marbles. The bag contains one red marble |(R),| one blue marble |(B),| one yellow marble |(Y)| and one green marble |(G).| How many possible outcomes exist?
We could enumerate the universe of possibilities |(\Omega),| eliminate the results that are equivalent, then count the remaining elements in this set. However, notice that this random experiment has the 3 characteristics below:
-
Order does not matter in this experiment.
-
The experiment is with replacement.
-
The experiment involves some of the elements of the starting set.
It is therefore most efficient to calculate the number of possible outcomes using the formula for the number of combinations with replacement. Since the starting set |\{R,B,Y,G\}| contains |4| elements |(n=4)| and we choose |2| of them |(k=2),| we calculate the following.
||\begin{aligned}\begin{gather}\text{Number of combinations}\\\text{with replacement}\end{gather}&=\dfrac{(n+k-1)!}{k!(n-1)!}\\&=\dfrac{(4+2-1)!}{2!(4-1)!}\\&=\dfrac{5!}{2!\times3!}\\&=\dfrac{5\times4\times3\times2\times1}{2\times1\times3\times2\times1}\\&=10\end{aligned}||
Answer: There are |10| possible outcomes in this random experiment.
We can represent the sample space of the previous example using a tree diagram. Simply eliminate the equivalent outcomes.