Finding the Rule of a Tangent Function

The rule of a tangent function is written as follows. ||f(x)=a\tan\big(b(x-h)\big)+k||

To find the equation of a tangent function from a graph, three points of information are needed.

1. The coordinates of the inflection point (the point of the curve where a change in curvature is observed, always located halfway between 2 consecutive asymptotes) of the tangent function provide the parameters |h| and |k.|
   
   ||P(x,y)=(h,k)||

2. The distance between 2 consecutive asymptotes corresponds to the period of the tangent function. The period is used to determine the absolute value of the parameter |b.|
   
   ||{\mid}b{\mid} =\dfrac{\pi}{\text{period}}||

3. The increasing and decreasing intervals of the tangent function makes it possible to determine the sign of the parameters |a| and |b.|
   
   If the tangent function is increasing between 2 consecutive asymptotes, then |ab>0,| meaning |a| and |b| are both positive or both negative.
   
   If the tangent function is decreasing between 2 consecutive asymptotes, then |ab<0,| meaning |a| and |b| have opposite signs.

1. Determine the values of |h| and |k| using the inflection point.

2. Determine the period to find the value of |b.|

3. Determine the signs of |a| and |b| according to the positive and negative intervals of the curve.

4. Determine the value of |a| by substituting the coordinates of a point into the equation.

In the following graph, find the rule of the tangent function.

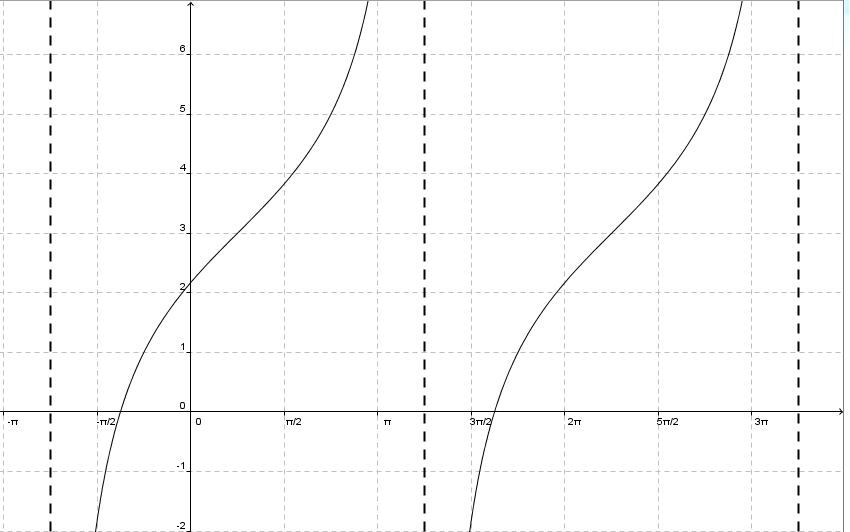
1. Find the values of |\boldsymbol{h}| and |\boldsymbol{k}|

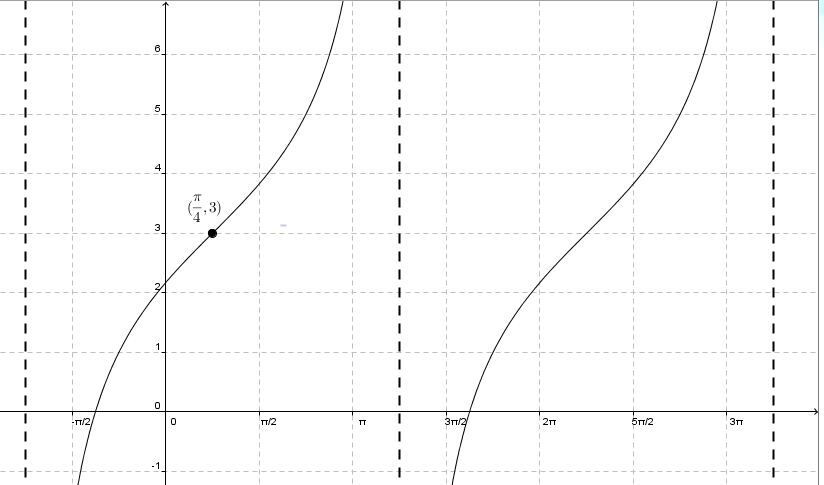
The inflection point of this function is located at |\left(\dfrac{\pi}{4},3\right).| Thus, the value of |h| will be |\dfrac{\pi}{4}| and the value of |k| will be |3.|

2. Determine the period to calculate the value of |\boldsymbol{b}|

||{\mid}b{\mid} = \dfrac{\pi}{\text{period}} = \dfrac{\pi}{2\pi}= \dfrac{1}{2}||

3. Determine the signs of |\boldsymbol{a}| and |\boldsymbol{b}| according to the positive and negative intervals of the curve

Between 2 consecutive asymptotes, notice that the function is increasing. Thus, the product |ab| is positive, i.e., the parameters |a| and |b| have the same sign. It is more practical to work with positive numbers when possible, so choose a positive value of |b|. By making this choice, a positive value of |a| will be calculated in the next step. If that is the case, it will confirm that the correct method was used.

4. Determine the value of |\boldsymbol{a}| by substituting the point’s coordinates in the equation

By using the precise coordinates of a point on the graph, the value of the parameter |a| can be determined.

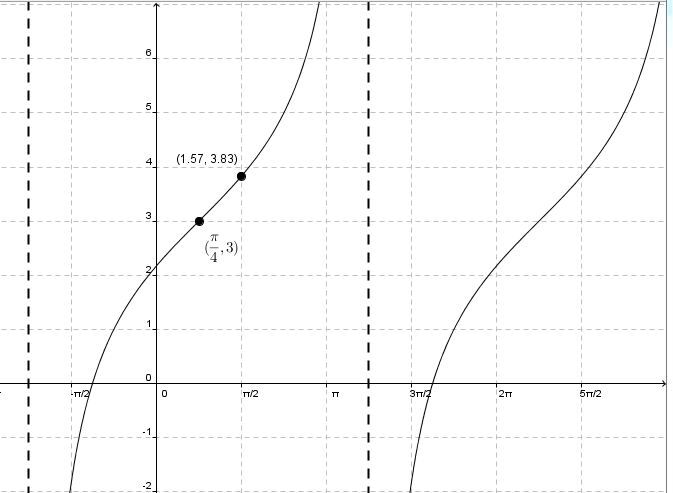
||\begin{align}
f(x) &= \color{blue}{a} \tan \dfrac{1}{2}\left(x-\dfrac{\pi}{4}\right)+3\\
3{.}83 &= \color{blue}{a} \tan \dfrac{1}{2}\left(1{.}57-\dfrac{\pi}{4}\right)+3\\
3{.}83 &\approx \color{blue}{a} \tan \dfrac{1}{2}(0{.}785)+3\\
3{.}83 &\approx \color{blue}{a} \tan (0{.}393)+3\\
3{.}83 &\approx \color{blue}{a}(0{.}414)+3\\
3{.}83 \color{red}{-3} &\approx \color{blue}{a}(0{.}414)+3 \color{red}{-3}\\
0{.}83 &\approx \color{blue}{a}(0{.}414)\\
\color{red}{\dfrac{\color{black}{0{.}83}}{0{.}414}} &\approx \color{red}{\dfrac{\color{blue}{a}\color{black}{(0{.}414)}}{0{.}414}} \\
2 &\approx \color{blue}{a}
\end{align}||

Answer: Thus, the equation of the function is: ||f(x)=2\tan\left(\dfrac{1}{2}\Big(x-\dfrac{\pi}{4}\Big)\right)+3||

1. Determine the period with the two known asymptotes.

2. Find the value of |{\mid}b{\mid}| and the sign of |b,| if possible.

3. Determine the value of the parameter |h.|

4. Build a system of equations with |a| and |k.|

5. Solve the system using the comparison method.

Find the equation of the tangent function passing through the points |(0\ , 1{.}455)| and |(-3\ , 3{.}557).| Furthermore, |x=-1-\pi| and |x=-1+\pi| are the equations of 2 consecutive asymptotes.

1. Determine the period with the 2 known asymptotes
   
   The difference between the two |x|-coordinates of the asymptotes gives the period. ||P = (-1+\pi)-(-1-\pi) = 2\pi||

2. Find the value of |\boldsymbol{{\mid}b{\mid}}| and the sign of |\boldsymbol{b}|, if possible
   
   When a tangent function is decreasing, the product |ab| is negative. If a positive value for |b| is chosen, it will result in the value of |a| being negative.
   
   Thus, |b = \dfrac{1}{2}.|

3. Determine the value of the parameter |\boldsymbol{h}|
   
   The value of the parameter |h| is determined by taking the average of the |x|-coordinates of the asymptotes. || h = \dfrac{-1+\pi + -1-\pi}{2} = -\dfrac{2}{2}=-1||

4. Build a system of equations with |\boldsymbol{a}| and |\boldsymbol{k}|
   
   Build a system of equations by replacing the known quantities in both equations. ||\begin{align} 3{.}557 &= a\tan\left(\dfrac{1}{2}(-3+1)\right)+k\\ 1{.}455 &= a\tan\left(\dfrac{1}{2}(0+1)\right)+k \end{align}||

5. Solve the system of equations
   
   Isolate |k| in both equations. ||\begin{align} 3{.}557 &= a\tan\left(\dfrac{1}{2}(-3+1\right)+k\\ 3{.}557 &= -1{.}557a + k\\ 3{.}557+1{.}557a &= k\\\\ 1{.}455 &= a\tan\left(\dfrac{1}{2}(0+1)\right)+k\\ 1{.}455 &= 0{.}546a + k\\ 1{.}455-0{.}546a &= k \end{align}||Move on to the comparison method. ||\begin{align}3{.}557+1{.}557a &= 1{.}455-0{.}546a \\ 2{.}102+1{.}557a &= -0{.}546\\ 2{.}102 &= -2{.}103a\\ -1 &\approx a \end{align}||Replace |a| in one of the 2 equations to find |k.| ||\begin{align} k &= 3{.}557+1{.}557a \\ k &= 3{.}557+1{.}557(-1) \\ k &\approx 2 \end{align}||

Answer: The rule of the function is |f(x)=-\tan\left(\dfrac{1}{2}(x+1)\right)+2.|