Trouver la règle d'une fonction tangente

La règle d'une fonction tangente s'écrit de la façon suivante.||f(x)=a\tan\big(b(x-h)\big)+k||

Pour trouver la règle d’une fonction tangente à partir d’un graphique, il faut connaitre 3 détails :

1. Les coordonnées d’un point d’inflexion (le point de la courbe où s’observe un changement de courbure situé à mi-chemin entre 2 asymptotes consécutives) de la fonction tangente fournissent directement les paramètres |h| et |k.| ||P(x,y)=(h,k)||

2. La distance entre 2 asymptotes consécutives correspond à la période de la fonction tangente. La période permet de déterminer la valeur absolue du paramètre |b.| ||{\mid}b{\mid} =\dfrac{\pi}{\text{période}}||

3. La variation de la fonction tangente permet de déterminer le signe des paramètres |a| et |b.|
   
   Si la fonction tangente est croissante entre 2 asymptotes consécutives, alors |ab>0,| c’est-à-dire que |a| et |b| sont tous les deux positifs ou tous les deux négatifs.
   
   Si la fonction tangente est décroissante entre 2 asymptotes consécutives, alors |ab<0,| c’est-à-dire que |a| et |b| sont de signes contraires.

1. Déterminer les valeurs de |h| et |k| à l’aide du point d’inflexion connu.

2. Déterminer la période pour trouver la valeur de |b.|

3. Déterminer les signes de |a| et |b| selon la variation de la courbe.

4. Déterminer la valeur de |a| en substituant les coordonnées d'un point dans l'équation.

À partir du graphique suivant, trouve la règle de la fonction tangente.
 

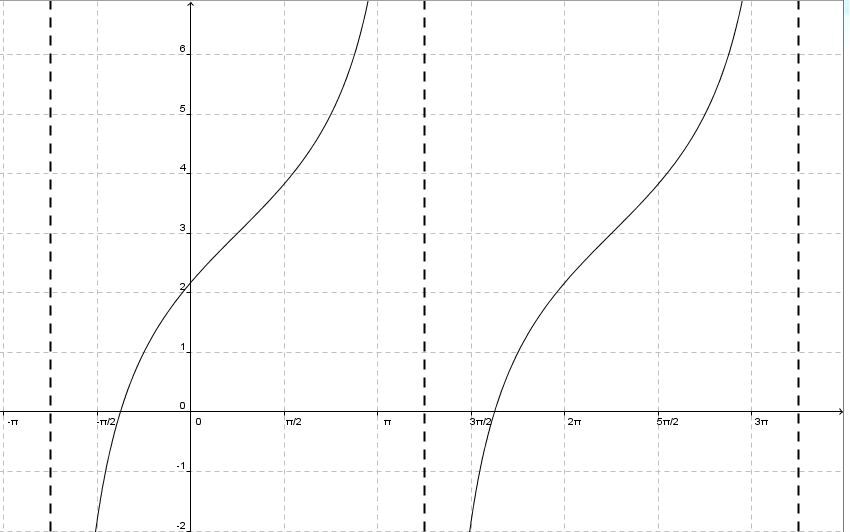
1. Trouver les valeurs de |\boldsymbol{h}| et |\boldsymbol{k}|

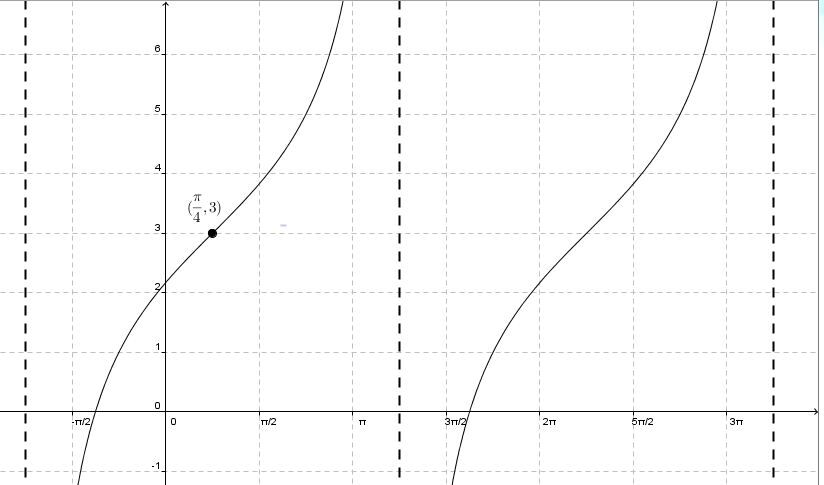
Le point d'inflexion de cette fonction est situé à |\left(\dfrac{\pi}{4},3\right).| Ainsi, la valeur de |h| sera de |\dfrac{\pi}{4}| et la valeur de |k| sera de |3.|

2. Déterminer la période pour calculer la valeur de |\boldsymbol{b}|

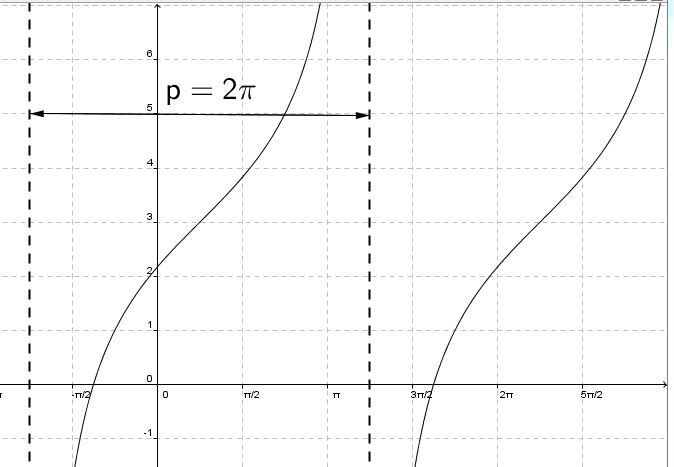
||{\mid}b{\mid} = \dfrac{\pi}{\text{période}} = \dfrac{\pi}{2\pi}= \dfrac{1}{2}||

3. Déterminer les signes de |\boldsymbol{a}| et |\boldsymbol{b}| selon la variation de la courbe

Entre 2 asymptotes consécutives, on remarque que la fonction est croissante. On en déduit que le produit |ab| est positif, c’est-à-dire que les paramètres |a| et |b| sont du même signe. Il est plus pratique de travailler avec les nombres positifs quand c’est possible, alors on choisit un |b| positif. En faisant ce choix, on devrait donc calculer un |a| positif à la prochaine étape. Si c’est bien le cas, on aura la confirmation que notre démarche est bonne.

4. Déterminer la valeur de |\boldsymbol{a}| en substituant les coordonnées d'un point dans l'équation

Si on a les coordonnées précises d’un point sur le graphique, on peut trouver la valeur du paramètre |a.|

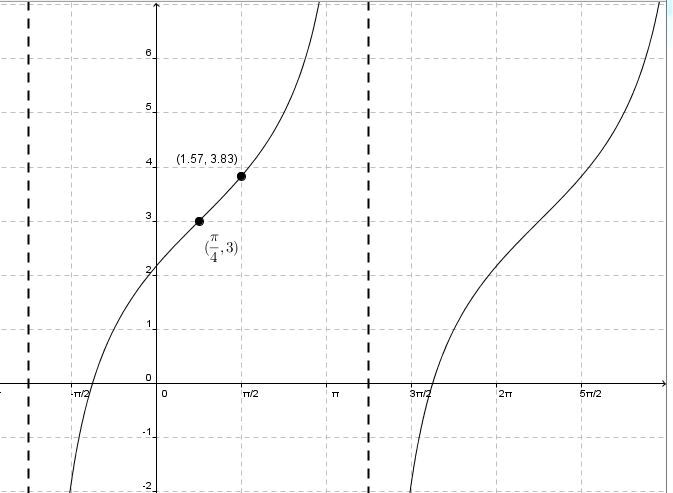
||\begin{align}
f(x) &= \color{blue}{a} \tan \dfrac{1}{2}\left(x-\dfrac{\pi}{4}\right)+3\\
3{,}83 &= \color{blue}{a} \tan \dfrac{1}{2}\left(1{,}57-\dfrac{\pi}{4}\right)+3\\
3{,}83 &\approx \color{blue}{a} \tan \dfrac{1}{2}(0{,}785)+3\\
3{,}83 &\approx \color{blue}{a} \tan (0{,}393)+3\\
3{,}83 &\approx \color{blue}{a}(0{,}414)+3\\
3{,}83 \color{red}{-3} &\approx \color{blue}{a}(0{,}414)+3 \color{red}{-3}\\
0{,}83 &\approx \color{blue}{a}(0{,}414)\\
\color{red}{\dfrac{\color{black}{0{,}83}}{0{,}414}} &\approx \color{red}{\dfrac{\color{blue}{a}\color{black}{(0{,}414)}}{0{,}414}} \\
2 &\approx \color{blue}{a}
\end{align}||

Réponse : La règle de la fonction est donc la suivante. ||f(x)=2\tan\left(\dfrac{1}{2}\Big(x-\dfrac{\pi}{4}\Big)\right)+3||

1. Déterminer la période avec les deux asymptotes connues

2. Trouver la valeur de |{\mid}b{\mid}| et le signe de |b,| si possible

3. Déterminer la valeur du paramètre |h|

4. Bâtir un système d'équations avec |a| et |k|

5. Résoudre le système précédent grâce à la méthode de comparaison

Trouve l'équation de la fonction tangente passant par les points |(0\ ; 1{,}455)| et |(-3\ ; 3{,}557)|. De plus, |x=-1-\pi| et |x=-1+\pi| sont les équations de deux asymptotes consécutives.

1. Déterminer la période avec les deux asymptotes connues
   
   La différence entre les 2 abscisses des asymptotes donne la valeur de la période. ||p = (-1+\pi)-(-1-\pi) = 2\pi||

2. Trouver la valeur de |\boldsymbol{{\mid}b{\mid}}| et le signe de |\boldsymbol{b}|, si possible
   
   Connaissant la période, il est possible de trouver la valeur absolue de |b.| || {\mid}b{\mid} =\dfrac{\pi}{\text{période}}= \dfrac{\pi}{2\pi} = \dfrac{1}{2}||De plus, la fonction est décroissante puisque, lorsque les abscisses augmentent, les ordonnées diminuent. En effet, il suffit de regarder les coordonnées des 2 points donnés.
   
   Quand une fonction tangente est décroissante, le produit |ab| est négatif. On peut choisir de prendre une valeur positive pour |b| et, ainsi, ce sera la valeur de |a| qui sera négative.
   
   De ce fait, |b = \dfrac{1}{2}.|

3. Déterminer la valeur du paramètre |\boldsymbol{h}|
   
   La valeur du paramètre |h| se détermine en faisant la moyenne des abscisses des asymptotes. || h = \dfrac{-1+\pi + -1-\pi}{2} = -\dfrac{2}{2}=-1||

4. Bâtir un système d'équations avec |\boldsymbol{a}| et |\boldsymbol{k}|
   
   On bâtit un système d'équations en remplaçant ce qu'on connait dans 2 équations. ||\begin{align} 3{,}557 &= a\tan\left(\dfrac{1}{2}(-3+1)\right)+k\\ 1{,}455 &= a\tan\left(\dfrac{1}{2}(0+1)\right)+k \end{align}||

5. Résoudre le système d'équations
   
   On isole |k| dans les 2 équations. ||\begin{align} 3{,}557 &= a\tan\left(\dfrac{1}{2}(-3+1\right)+k\\ 3{,}557 &= -1{,}557a + k\\ 3{,}557+1{,}557a &= k\\\\ 1{,}455 &= a\tan\left(\dfrac{1}{2}(0+1)\right)+k\\ 1{,}455 &= 0{,}546a + k\\ 1{,}455-0{,}546a &= k \end{align}||On passe à la méthode de comparaison. ||\begin{align}3{,}557+1{,}557a &= 1{,}455-0{,}546a \\ 2{,}102+1{,}557a &= -0{,}546\\ 2{,}102 &= -2{,}103a\\ -1 &\approx a \end{align}||On remplace |a| dans l'une des 2 équations pour trouver |k.| ||\begin{align} k &= 3{,}557+1{,}557a \\ k &= 3{,}557+1{,}557(-1) \\ k &\approx 2 \end{align}||

Réponse : La règle de la fonction est |f(x)=-\tan\left(\dfrac{1}{2}(x+1)\right)+2.|