We distinguish between 2 different cases when looking for the rule of a square root function in the standard form: either its vertex is located at the origin of the Cartesian plane, or it is located elsewhere.
In both cases, the simplified form of the rule can be used. In this way, parameter |\color{#EC0000}{b}| will only be |\color{#EC0000}{-1}| or |\color{#EC0000}{1}|.
The vertex is at the origin
||a\sqrt{\color{#EC0000}{b}x}\Rightarrow a\sqrt{\color{#EC0000}{\pm}x}||
The vertex is not at the origin
||a\sqrt{\color{#EC0000}{b}(x-h)}+k\Rightarrow a\sqrt{\color{#EC0000}{\pm}(x-h)}+k||
It can be proven why, in the square root function, it is possible to use the simplified form of the rule by assuming parameter |\color{#EC0000}{b}| is equal to |\color{#EC0000}{\pm1}.|
Consider |f(x)=a\sqrt{\color{#EC0000}{b}(x-h)}+k.| Using the properties of the radicals, we can perform the following calculations.
||\begin{gather}\begin{aligned}f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{b}(x-h)}+k\\f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\pm\vert b\vert}(x-h)}+k\\f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\vert b\vert}\vphantom{(}}\sqrt{\color{#EC0000}{\pm}(x-h)}+k\\f(x)&=\color{#C58AE1}{\text{a}}\sqrt{\color{#EC0000}{\pm}(x-h)}+k\end{aligned}\\\text{where}\\\color{#C58AE1}{\text{a}}=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\vert b\vert}}\end{gather}||
The following is the procedure to find the rule of a square root function when the vertex is at the origin of the Cartesian plane and the coordinates of another point are known.
-
Determine the value of |\color{#EC0000}{b}| based on the role of the parameters. If the curve lies to the right of the vertex, then |\color{#EC0000}{b}=\color{#EC0000}{1}.| However, if the curve lies to the left of the vertex, then |\color{#EC0000}{b}=\color{#EC0000}{-1}.|
-
Replace |\color{#3A9A38}{x}| and |\color{#3A9A38}{f(x)}| with the coordinates of a point other than the vertex to form an equation.
-
Calculate the value of parameter |\color{#3b87CD}{a}.|
-
Give the rule of the function.
Determine the rule for the following square root function.

-
Determine if |b| is worth |1| or |-1|
Point |(\color{#3A9A38}{-9},\color{#3A9A38}{15})| is to the left of the vertex, which implies that |\color{#EC0000}{b}| is negative.
||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}x}\\f(x)&=a\sqrt{\color{#EC0000}{-1}x}\\f(x)&=a\sqrt{-x}\\\end{align}|| -
Replace |x| and |f(x)| with the coordinates of a point
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{-\color{#3A9A38}{x}}\\\color{#3A9A38}{15}&=a\sqrt{-\color{#3A9A38}{-9}}\end{align}|| -
Calculate the value of parameter |a|
||\begin{align}15&=\color{#3b87CD}{a}\sqrt{--9}\\15&=\color{#3b87CD}{a}\sqrt{9}\\15&=3\color{#3b87CD}{a}\\\color{#3b87CD}{5}&=\color{#3b87CD}{a}\end{align}|| -
Give the rule
The rule for this square root function is |f(x)=5\sqrt{-x}.|
The following is the procedure to find the rule of a square root function when the vertex is not at the origin of the Cartesian plane and the coordinates of another point are known.
-
Replace |\color{#51B6C2}{h}| and |\color{#FA7921}{k}| in the rule with the coordinates of the vertex.
-
Determine the value of |\color{#EC0000}{b}| based on the role of the parameters. If the curve lies to the right of the vertex, then |\color{#EC0000}{b}=\color{#EC0000}{1}.| However, if the curve lies to the left of the vertex, then |\color{#EC0000}{b}=\color{#EC0000}{-1}.|
-
Replace |\color{#3A9A38}{x}| and |\color{#3A9A38}{f(x)}| with the coordinates of a point other than the vertex to form an equation.
-
Calculate the value of parameter |\color{#3b87CD}{a}.|
-
Give the rule of the function.
Determine the rule for the following square root function.
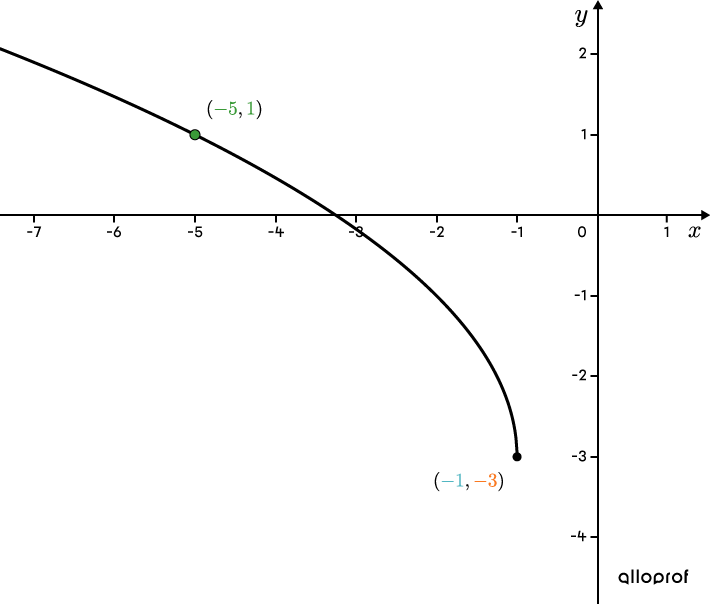
-
Replace |h| and |k| with the vertex coordinates
||\begin{align}f(x)&=a\sqrt{b(x-\color{#51B6C2}{h})}+\color{#FA7921}{k}\\f(x)&=a\sqrt{b(x-\color{#51B6C2}{-1})}+\color{#FA7921}{-3}\\f(x)&=a\sqrt{b(x+1)}-3\end{align}|| -
Determine if |b| is worth |1| or |-1|
Point |(\color{#3A9A38}{-5},\color{#3A9A38}{1})| is to the left of the vertex, which implies that |\color{#EC0000}{b}| is negative.
||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}(x+1)}-3\\f(x)&=a\sqrt{\color{#EC0000}{-1}(x+1)}-3\\f(x)&=a\sqrt{-(x+1)}-3\end{align}|| -
Replace |x| and |f(x)| with the coordinates of a point
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{-(\color{#3A9A38}{x}+1)}-3\\\color{#3A9A38}{1}&=a\sqrt{-(\color{#3A9A38}{-5}+1)}-3\end{align}|| -
Calculate the value of parameter |a|
||\begin{align}1&=\color{#3b87CD}{a}\sqrt{-(-5+1)}-3\\1&=\color{#3b87CD}{a}\sqrt{4}-3\\1&=2\color{#3b87CD}{a}-3\\4&=2\color{#3b87CD}{a}\\\color{#3b87CD}{2}&=\color{#3b87CD}{a}\end{align}|| -
Give the rule
The rule for this square root function is |f(x)=2\sqrt{-(x+1)}-3.|
Sometimes, one of the vertex coordinates is not known. In this case, the coordinates of a second point on the curve are needed to form a system of 2 equations with 2 unknowns. The following example shows how to solve this kind of problem.
Determine the rule for the following square root function.

-
Replace |h|
||\begin{align}f(x)&=a\sqrt{b(x-\color{#51B6C2}{h})}+\color{#FA7921}{k}\\f(x)&=a\sqrt{b(x-\color{#51B6C2}{5})}+\color{#FA7921}{k}\end{align}|| -
Determine if |b| is worth |1| or |-1|
The two points provided are to the right of the vertex, which implies that |\color{#EC0000}{b}| is positive.
||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}(x-5)}+k\\f(x)&=a\sqrt{\color{#EC0000}{1}(x-5)}+k\\f(x)&=a\sqrt{x-5}+k\end{align}|| -
Replace |x| and |f(x)| with the coordinates of 2 points
Since the parameters |\color{#3B87CD}{a}| and |\color{#FA7921}{k}| are unknown, we must form a system of 2 equations.
First equation
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{\color{#3A9A38}{x}-5}+k\\ \color{#3A9A38}{-8}&=a\sqrt{\color{#3A9A38}{9}-5}+k\end{align}||
Second equation
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{\color{#3A9A38}{x}-5}+k\\ \color{#3A9A38}{-15}&=a\sqrt{\color{#3A9A38}{14}-5}+k\end{align}||
-
Solve the system of equations to find the value of |a| and |k|
The system of equations can now be solved. Isolate |\color{#FA7921}{k}| in the first equation, and then use the substitution method.||\begin{align}-8&=\color{#3B87CD}{a}\sqrt{9-5}+\color{#FA7921}{k}\\-8&=\color{#3B87CD}{a}\sqrt{4}+\color{#FA7921}{k}\\-8&=2\color{#3B87CD}{a}+\color{#FA7921}{k}\\\color{#FA7921}{-8-2a}&=\color{#FA7921}{k}\\\end{align}||
Substituting |\color{#FA7921}{k}| in the second equation results in the following.||\begin{align}-15&=\color{#3B87CD}{a}\sqrt{14-5}+\color{#FA7921}{k}\\-15&=\color{#3B87CD}{a}\sqrt{9}\color{#FA7921}{-8-2a}\\-7&=3\color{#3B87CD}{a}-2\color{#3B87CD}{a}\\\color{#3B87CD}{-7}&=\color{#3B87CD}{a}\\\end{align}||
Finally, by replacing |\color{#3B87CD}{a}| in the first equation, we get the value of |\color{#FA7921}{k}.|||\begin{align}-8-2\color{#3B87CD}{a}&=\color{#FA7921}{k}\\-8-2(\color{#3B87CD}{-7})&=\color{#FA7921}{k}\\\color{#FA7921}{6}&=\color{#FA7921}{k}\end{align}||
-
Give the rule
The rule for this square root function is |f(x)=-7\sqrt{x-5}+6.|