On distingue 2 cas différents lorsqu’on cherche la règle d’une fonction racine carrée sous la forme canonique : soit son sommet est situé à l’origine du plan cartésien, soit son sommet est situé ailleurs.
Dans les deux cas, on peut utiliser la forme simplifiée de la règle. De cette façon, le paramètre |\color{#EC0000}{b}| prend seulement |\color{#EC0000}{-1}| ou |\color{#EC0000}{1}| comme valeur.
Le sommet est à l’origine
||a\sqrt{\color{#EC0000}{b}x}\Rightarrow a\sqrt{\color{#EC0000}{\pm}x}||
Le sommet n’est pas à l’origine
||a\sqrt{\color{#EC0000}{b}(x-h)}+k\Rightarrow a\sqrt{\color{#EC0000}{\pm}(x-h)}+k||
On peut démontrer la raison pour laquelle, dans la fonction racine carrée, il est possible d’utiliser la forme simplifiée de la règle en supposant que le paramètre |\color{#EC0000}{b}| est égal à |\color{#EC0000}{\pm1}.|
Soit |f(x)=a\sqrt{\color{#EC0000}{b}(x-h)}+k.| En utilisant les propriétés des racines, on peut procéder aux manipulations suivantes.||\begin{gather}\begin{aligned}f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{b}(x-h)}+k\\f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\pm\vert b\vert}(x-h)}+k\\f(x)&=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\vert b\vert}\vphantom{(}}\sqrt{\color{#EC0000}{\pm}(x-h)}+k\\f(x)&=\color{#C58AE1}{\text{a}}\sqrt{\color{#EC0000}{\pm}(x-h)}+k\end{aligned}\\\text{où}\\\color{#C58AE1}{\text{a}}=\color{#3B87CD}{a}\sqrt{\color{#EC0000}{\vert b\vert}}\end{gather}||
Voici la démarche à suivre pour trouver la règle d’une fonction racine carrée lorsque son sommet est à l’origine du plan cartésien et que l’on connait les coordonnées d’un autre point de la fonction.
-
Déduire la valeur de |\color{#EC0000}{b}| en se basant sur le rôle des paramètres. Si la courbe se trouve à droite du sommet, alors |\color{#EC0000}{b}=\color{#EC0000}{1}.| Autrement, si la courbe se trouve à gauche du sommet, alors |\color{#EC0000}{b}=\color{#EC0000}{-1}.|
-
Remplacer |\color{#3A9A38}{x}| et |\color{#3A9A38}{f(x)}| par les coordonnées d’un point autre que le sommet pour former une équation.
-
Calculer la valeur du paramètre |\color{#3b87CD}{a}.|
-
Donner la règle de la fonction.
Détermine la règle de la fonction racine carrée ci-dessous.

-
Déduire si |b| vaut |1| ou |-1|
Le point |(\color{#3A9A38}{-9},\color{#3A9A38}{15})| est à gauche du sommet, ce qui implique que |\color{#EC0000}{b}| est négatif.||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}x}\\f(x)&=a\sqrt{\color{#EC0000}{-1}x}\\f(x)&=a\sqrt{-x}\\\end{align}|| -
Remplacer |x| et |f(x)| par les coordonnées d’un point
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{-\color{#3A9A38}{x}}\\\color{#3A9A38}{15}&=a\sqrt{-\color{#3A9A38}{-9}}\end{align}|| -
Calculer la valeur du paramètre |a|
||\begin{align}15&=\color{#3b87CD}{a}\sqrt{--9}\\15&=\color{#3b87CD}{a}\sqrt{9}\\15&=3\color{#3b87CD}{a}\\\color{#3b87CD}{5}&=\color{#3b87CD}{a}\end{align}|| -
Donner la règle
La règle de cette fonction racine carrée est |f(x)=5\sqrt{-x}.|
Voici la démarche à suivre pour trouver la règle d’une fonction racine carrée lorsque son sommet n’est pas à l’origine du plan cartésien et qu’on connait les coordonnées d’un autre point de la fonction.
-
Remplacer |\color{#51B6C2}{h}| et |\color{#FA7921}{k}| dans la règle par les coordonnées du sommet.
-
Déduire la valeur de |\color{#EC0000}{b}| en se basant sur le rôle des paramètres. Si la courbe se trouve à droite du sommet, alors |\color{#EC0000}{b}=\color{#EC0000}{1}.| Autrement, si la courbe se trouve à gauche du sommet, alors |\color{#EC0000}{b}=\color{#EC0000}{-1}.|
-
Remplacer |\color{#3A9A38}{x}| et |\color{#3A9A38}{f(x)}| par les coordonnées d’un point autre que le sommet pour former une équation.
-
Calculer la valeur du paramètre |\color{#3b87CD}{a}.|
-
Donner la règle de la fonction.
Détermine la règle de la fonction racine carrée ci-dessous.
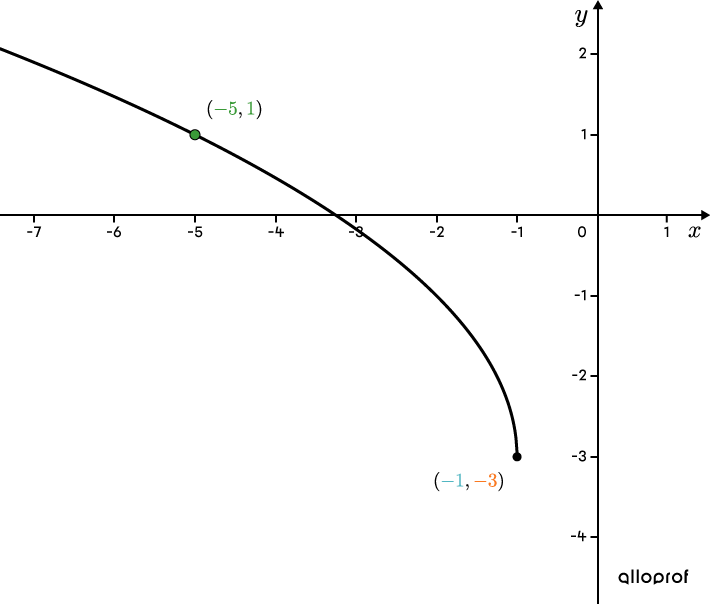
-
Remplacer |h| et |k| par les coordonnées du sommet
||\begin{align}f(x)&=a\sqrt{b(x-\color{#51B6C2}{h})}+\color{#FA7921}{k}\\f(x)&=a\sqrt{b(x-\color{#51B6C2}{-1})}+\color{#FA7921}{-3}\\f(x)&=a\sqrt{b(x+1)}-3\end{align}|| -
Déduire si |b| vaut |1| ou |-1|
Le point |(\color{#3A9A38}{-5},\color{#3A9A38}{1})| est à gauche du sommet, ce qui implique que |\color{#EC0000}{b}| est négatif.||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}(x+1)}-3\\f(x)&=a\sqrt{\color{#EC0000}{-1}(x+1)}-3\\f(x)&=a\sqrt{-(x+1)}-3\end{align}|| -
Remplacer |x| et |f(x)| par les coordonnées d’un point
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{-(\color{#3A9A38}{x}+1)}-3\\\color{#3A9A38}{1}&=a\sqrt{-(\color{#3A9A38}{-5}+1)}-3\end{align}|| -
Calculer la valeur du paramètre |a|
||\begin{align}1&=\color{#3b87CD}{a}\sqrt{-(-5+1)}-3\\1&=\color{#3b87CD}{a}\sqrt{4}-3\\1&=2\color{#3b87CD}{a}-3\\4&=2\color{#3b87CD}{a}\\\color{#3b87CD}{2}&=\color{#3b87CD}{a}\end{align}|| -
Donner la règle
La règle de la fonction racine carrée est |f(x)=2\sqrt{-(x+1)}-3.|
Il arrive parfois qu’une des coordonnées du sommet ne soit pas connue. Dans cette situation, on a besoin des coordonnées d’un deuxième point sur la courbe afin de former un système de 2 équations à 2 inconnues. L’exemple suivant montre comment résoudre ce genre de problème.
Détermine la règle de la fonction racine carrée ci-dessous.

-
Remplacer |h|
||\begin{align}f(x)&=a\sqrt{b(x-\color{#51B6C2}{h})}+\color{#FA7921}{k}\\f(x)&=a\sqrt{b(x-\color{#51B6C2}{5})}+\color{#FA7921}{k}\end{align}|| -
Déduire si |b| vaut |1| ou |-1|
Les deux points fournis sont à droite du sommet, ce qui implique que |\color{#EC0000}{b}| est positif.||\begin{align}f(x)&=a\sqrt{\color{#EC0000}{b}(x-5)}+k\\f(x)&=a\sqrt{\color{#EC0000}{1}(x-5)}+k\\f(x)&=a\sqrt{x-5}+k\end{align}|| -
Remplacer |x| et |f(x)| par les coordonnées de 2 points
Puisque les paramètres |\color{#3B87CD}{a}| et |\color{#FA7921}{k}| sont inconnus, on doit former un système de 2 équations.
Première équation
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{\color{#3A9A38}{x}-5}+k\\ \color{#3A9A38}{-8}&=a\sqrt{\color{#3A9A38}{9}-5}+k\end{align}||
Deuxième équation
||\begin{align}\color{#3A9A38}{f(x)}&=a\sqrt{\color{#3A9A38}{x}-5}+k\\ \color{#3A9A38}{-15}&=a\sqrt{\color{#3A9A38}{14}-5}+k\end{align}||
-
Résoudre le système d’équations pour trouver la valeur de |a| et |k|
On peut maintenant résoudre le système d’équations. On isole |\color{#FA7921}{k}| dans la première équation pour ensuite utiliser la méthode de substitution.||\begin{align}-8&=\color{#3B87CD}{a}\sqrt{9-5}+\color{#FA7921}{k}\\-8&=\color{#3B87CD}{a}\sqrt{4}+\color{#FA7921}{k}\\-8&=2\color{#3B87CD}{a}+\color{#FA7921}{k}\\\color{#FA7921}{-8-2a}&=\color{#FA7921}{k}\\\end{align}||En substituant |\color{#FA7921}{k}| dans la deuxième équation, on a :||\begin{align}-15&=\color{#3B87CD}{a}\sqrt{14-5}+\color{#FA7921}{k}\\-15&=\color{#3B87CD}{a}\sqrt{9}\color{#FA7921}{-8-2a}\\-7&=3\color{#3B87CD}{a}-2\color{#3B87CD}{a}\\\color{#3B87CD}{-7}&=\color{#3B87CD}{a}\\\end{align}||Finalement, en remplaçant |\color{#3B87CD}{a}| dans la première équation, on obtient la valeur de |\color{#FA7921}{k}| :||\begin{align}-8-2\color{#3B87CD}{a}&=\color{#FA7921}{k}\\-8-2(\color{#3B87CD}{-7})&=\color{#FA7921}{k}\\\color{#FA7921}{6}&=\color{#FA7921}{k}\end{align}|| -
Donner la règle
La règle de cette fonction racine carrée est |f(x)=-7\sqrt{x-5}+6.|