Solving a Square Root Equation or Inequality

An irrational equation or inequality contains a variable under a root.

There are 2 restrictions that must always be taken into account when solving an equation or an inequality containing a square root.

1. A square root is always greater than or equal to |0.|
   ||\sqrt{a}\ge0||

2. The term under a square root, called the radicand, is always greater than or equal to |0.|
   ||a\ge0||

Referring to the restrictions makes it possible to validate the solutions obtained when solving the equation or inequality.

1. Isolate the square root(s).

2. Check if the square root(s) is/are greater than or equal to |0| and calculate the restriction(s), if necessary.

3. Square both sides of the equation.

4. Solve the equation.

5. Verify the solution(s).

6. Give the solution set.

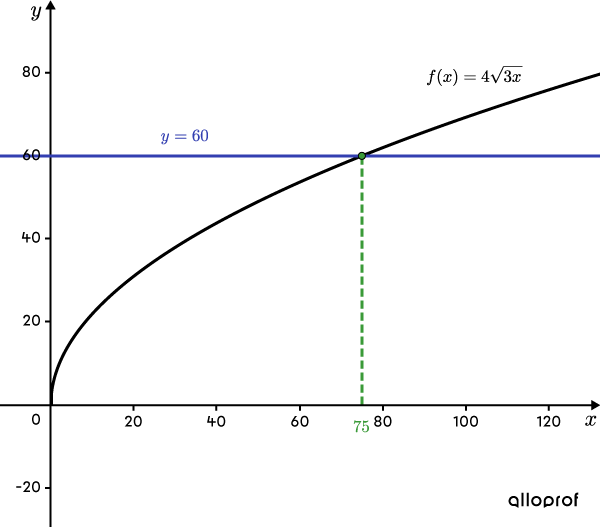
Solve the equation |4\sqrt{3x}=60.|

1. Isolate the square root
   ||\begin{align}4\sqrt{3x}&=60\\\sqrt{3x}&=15\end{align}||

2. Calculate the restrictions
   Note that |\sqrt{3x}| is greater than |0,| because it is equal to |15.| It suggests that there is at least one solution. We find the restriction so the term under the root is positive.
   ||\begin{align}3x&\ge0\\x&\ge0\end{align}||

3. Square both sides of the equation
   ||\begin{align}\sqrt{3x}&=15\\\color{#EC0000}{(\color{black}{\sqrt{3x}})^2}&=15^{\color{#EC0000}{2}}\end{align}||

4. Solve the equation
   ||\begin{align}3x&=225\\\color{#3A9A38}{x}&=\color{#3A9A38}{75}\end{align}||

5. Verify the solution
   The restriction |x\ge0| calculated in step 2 is respected because |\color{#3A9A38}{75}\ge0.|

6. Give the solution

There are 2 ways to verify the solution in step 5.

1. Ensure that the solution meets the restriction determined in step 2, as shown in the previous example.

2. Substitute the solution into the original equation. In the previous example, variable |x| is replaced in the equation |4\sqrt{3x}=60| and the left side of the equation is equivalent to the right side.

||\begin{align}4\sqrt{3\color{#EC0000}{x}}&=60\\4\sqrt{3(\color{#EC0000}{75})}&\overset{?}{=}60\\4\sqrt{225}&\overset{?}{=}60\\60&=60\end{align}||
The last equality is true, confirming that the solution |x=75| is valid.

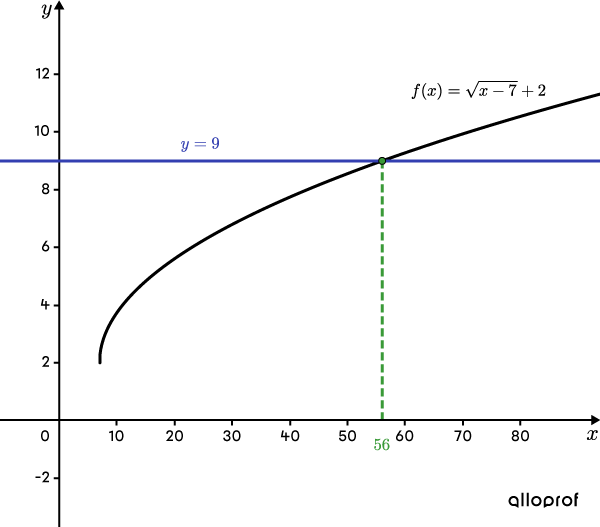
Solve the equation |\sqrt{x-7}+2=9.|

1. Isolate the square root
   ||\begin{align}\sqrt{x-7}+2&=9\\\sqrt{x-7}&=7\end{align}||

2. Calculate the restrictions
   Note that |\sqrt{x-7}| is greater than |0|, because it is equal to |7.| It suggests there is at least one solution. For the second restriction, we have:
   ||\begin{align}x-7&\ge0\\x&\ge7\end{align}||

3. Square both sides of the equation
   ||\begin{align}\sqrt{x-7}&=7\\\color{#EC0000}{(\color{black}{\sqrt{x-7}})^2}&=7^{\color{#EC0000}{2}}\end{align}||

4. Solve the resulting equation
   ||\begin{align}x-7&=49\\\color{#3A9A38}{x}&=\color{#3A9A38}{56}\end{align}||

5. Verify the solution obtained
   The restriction |x\ge7| calculated in step 2 is respected, because |\color{#3A9A38}{56}\ge7.|

6. Give the solution

Solve the equation |2\sqrt{x+1}+3=1.|

1. Isolate the square root
   ||\begin{align}2\sqrt{x+1}+3&=1\\2\sqrt{x+1}&=-2\\\sqrt{x+1}&=-1\end{align}||

2. Calculate the restrictions
   A square root must always be greater than or equal to |0,| which is not the case here, because we obtain the equation |\sqrt{x+1}=-1.|

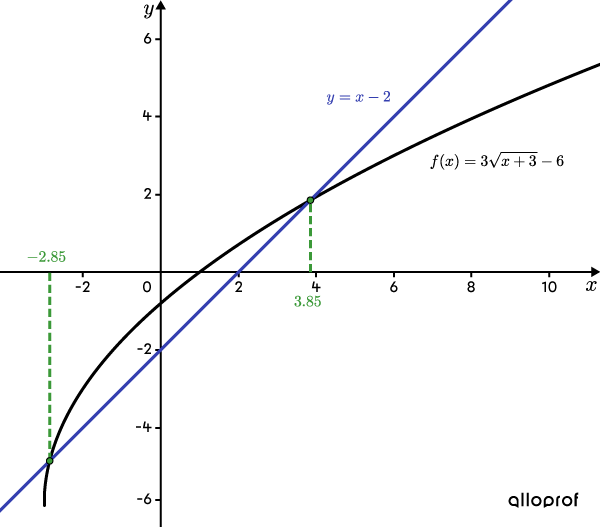
Solve the equation |3\sqrt{x+3}-6=x-2.|

1. Isolate the square root
   ||\begin{align}3\sqrt{x+3}-6&=x-2\\3\sqrt{x+3}&=x+4\\\sqrt{x+3}&=\dfrac{x+4}{3}\end{align}||

2. Calculate the restrictions
   Note that |\sqrt{x+3}| is greater than or equal to |0| only when |\dfrac{x+4}{3}| is as well. Therefore, it is necessary to determine the restriction.
   ||\begin{align}\dfrac{x+4}{3}&\ge0\\x+4&\ge0\\x&\ge-4\end{align}||
   When |x\ge-4,| it suggests that there is at least one solution. We also need to find the restriction so that the term under the root is positive.
   ||\begin{align}x+3&\ge0\\x&\ge-3\end{align}||
   We have |2| restrictions where |x\ge-4| and |x\ge-3.| Sometimes, like here, one of the |2| restrictions is unnecessary. So, it is sufficient to use only the |x\ge-3,| restriction, because a number |x| that is more than |-3| is greater than |-4.| Keep only |x\ge-3.|

3. Square both sides of the equation
   ||\begin{align}\sqrt{x+3}&=\dfrac{x+4}{3}\\\color{#EC0000}{(\color{black}{\sqrt{x+3}})^2}&=\color{#EC0000}{\left(\color{black}{\dfrac{x+4}{3}}\right)^2}\end{align}||

4. Solve the resulting equation
   This is a second-degree equation, so it is best to transform it to equal |0.|||\begin{align}x+3&=\dfrac{x^2+8x+16}{9}\\9(x+3)&=x^2+8x+16\\9x+27&=x^2+8x+16\\0&=x^2-x-11\end{align}||
   Then use the quadratic formula to find the values of |x.|
   ||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(1)(-11)}}{2(1)}\\&=\dfrac{1\pm\sqrt{45}}{2}\\\color{#3A9A38}{x}&\in\{\color{#3A9A38}{-2.85},\color{#3A9A38}{3.85}\}\end{align}||

5. Check the solutions
   The restriction |x\ge-3| calculated in step 2 is respected in both cases, because |\color{#3A9A38}{-2.85}\ge-3| and |\color{#3A9A38}{3.85}\ge-3.|

6. Give the solution set

Solve the equation |\sqrt{x-3}+\sqrt{x}=1.|

1. Isolate one of the square roots
   ||\begin{align}\sqrt{x-3}+\sqrt{x}&=1\\\sqrt{x-3}&=1-\sqrt{x}\end{align}||

2. Calculate the restrictions
   Note that |\sqrt{x-3}| is greater than |0| only when |1-\sqrt{x}| is as well. So, it is necessary to determine the restriction.
   ||\begin{align}1-\sqrt{x}&\ge0\\1&\ge\sqrt{x}\\1^\color{#EC0000}{2} &\ge\color{#EC0000}{(\color{black}{\sqrt{x}})^2}\\1&\ge x\end{align}||
   It suggests there is at least one solution when |x\le1.| Find the restriction so the term under the root is positive.
   ||\begin{align}x-3&\ge0\\x&\ge3\end{align}||
   We have |2| conflicting restrictions where |x\le1| and |x\ge3.| Since there is no number less than |1| and more than |3,| there is no solution to the equation |\sqrt{x-3}+\sqrt{x}=1.|

1. Replace the inequality symbol with the equal symbol.

2. Isolate the square root.

3. Check if the square root is greater than or equal to |0| and calculate the restriction, if necessary.

4. Square both sides of the equation.

5. Solve the equation.

6. Verify the solution set of the equation.

7. Determine the solution set of the inequality using a graph or a number line.

Solve the inequality |\sqrt{x-3}>2.|

1. Replace the inequality symbol with the equal symbol
   ||\sqrt{x-3}=2||

2. Isolate the square root
   The square root is already isolated.

3. Calculate the restrictions
   Note that |\sqrt{x-3}| is greater than |0|, because it is equal to |2.| It suggests there is at least one solution. As for the restriction under the root, we have:
   ||\begin{align}x-3&\ge0\\x&\ge3\end{align}||

4. Square both sides of the equation
   ||\begin{align}\sqrt{x-3}&=2\\\color{#EC0000}{(\color{black}{\sqrt{x-3}})^2}&=\color{#EC0000}{\left(\color{black}{2}\right)^2}\end{align}||

5. Solve the equation
   ||\begin{align}x-3&=4\\x&=7\end{align}||

6. Validate the solution of the equation
   The value |x=7| is valid because it respects the restriction |x\ge3| calculated in step 3.

7. Determine the solution set of the inequality
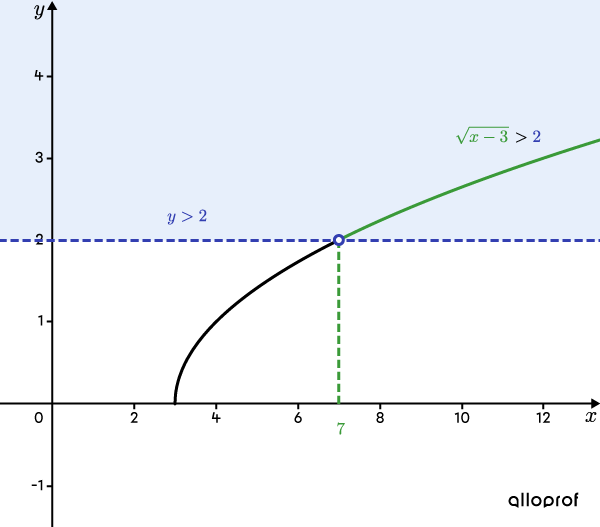
   To determine the solution set, we can draw the graph of the square root function |f(x)=\sqrt{x-3}.| Here's how.

Graphing the function to determine the solution set in step 7 is not the only option. Sometimes, a number line is enough to get the same conclusion. Here's how.

First, we draw a number line and represent, with a solid point, the restriction |x\ge3| determined in step 3. Next, place an empty point at |x=7,| the solution obtained in step 5. The point is empty, because the radical |\sqrt{x-3}| is strictly greater than |2.|

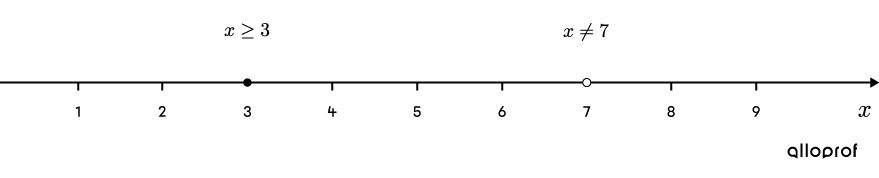
The 2 values of |x| divide the number line into 3 intervals: |]-\infty, 3],| |[3,7[,| and |]7,+\infty[.| It is necessary to validate a random value in each section of the initial inequality. However, it is not necessary to check the interval |]-\infty,3[,| because, as demonstrated in step 3, the solution to the inequality must be greater than or equal to |3.|

• For |[3,7[,| use |x=5.|

||\begin{align}\sqrt{\color{#3A9A38}{x}-3}&>2\\\sqrt{\color{#3A9A38}{5}-3}&\stackrel{?}{>}2\\\sqrt{2}&\not>2\end{align}||
This is impossible and suggests the interval |[3,7[| is not part of the solution set.

• For |]7,+\infty[,| use |x=9.|

The answer obtained is |\sqrt{6}>2,| which is true. Therefore, interval |]7,+\infty[| is part of the solution set.

On the number line, we can finally colour the section that corresponds to the solution set.

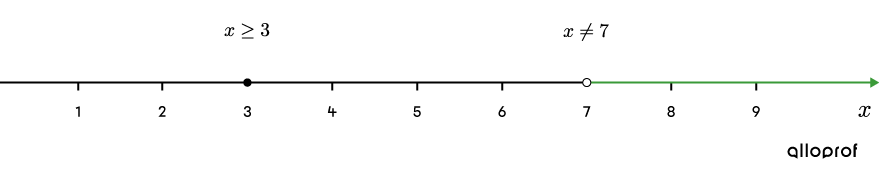
Therefore, as with the graph method, we determine that the solution set of the inequality |\sqrt{x-3}>2| is |]7,+\infty[.|

Solve the inequality |\sqrt{2x-5}\le5.|

1. Replace the inequality symbol with an equal symbol
   ||\sqrt{2x-5}=5||

2. Isolate the square root
   The square root is already isolated.

3. Calculate the restrictions
   Note that |\sqrt{2x-5}| is greater than |0|, because it is equal to |5.| It suggests there is at least one solution. As for the restriction under the root, we have:
   ||\begin{align}2x-5&\ge0\\2x&\ge5\\x&\ge\dfrac{5}{2}\end{align}||
   On a number line, the restriction is indicated with a solid point.

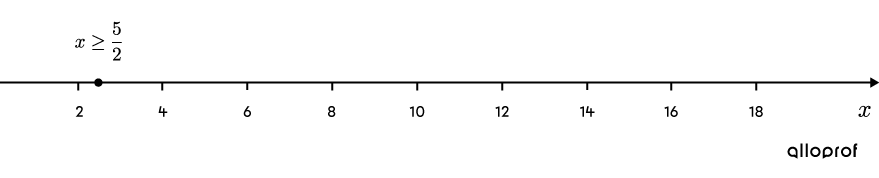
4. Square both sides of the equation
   ||\begin{align}\sqrt{2x-5}&=5\\\color{#EC0000}{(\color{black}{\sqrt{2x-5}})^2}&=\color{#EC0000}{\left(\color{black}{5}\right)^2}\end{align}||

5. Solve the equation
   ||\begin{align}2x-5&=25\\2x&=30\\x&=15\end{align}||
   Add a solid point to |x=15| on the number line. The point is solid, because the symbol for the inequality is |\le.|

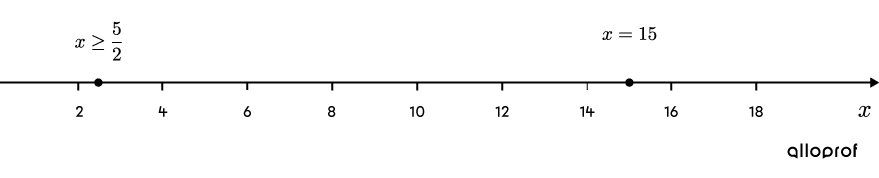
6. Verify the solution of the equation
   The value |x=15| is valid, because it respects the restriction |x\ge\dfrac{5}{2}| calculated in step 3.

7. Determine the solution set of the inequality
   Now, check which interval is part of the solution set by replacing |x| in the original inequality. It is not necessary to check the interval |\left]-\infty,\dfrac{5}{2}\right[,| because it was proven in step 3 that the solution of the inequality is not in this interval.
   
   Then, take a value of |x| between |\dfrac{5}{2}| and |15,| for example, |x=10.| We have:
   ||\begin{align}\sqrt{2\color{#EC0000}{x}-5}&\le5\\\sqrt{2(\color{#EC0000}{10})-5}&\stackrel{?}{\le}5\\\sqrt{15}&\stackrel{?}{\le}5\\3.87&\le5\end{align}||
   The inequality is true, suggesting the interval |\left[\dfrac{5}{2},15\right]| is part of the solution set. Similarly, by replacing |x| by a number greater than |15,| such as |x=20,| it can be determined that the interval |]15,+\infty[| is not part of the solution set.

The solution set of the inequality |\sqrt{2x-5}\le5| is |\left[\dfrac{5}{2},15\right].|

Here is an example of when the square root function intersects a linear function. In this case, solve a second-degree equation and keep only one of the two solutions.

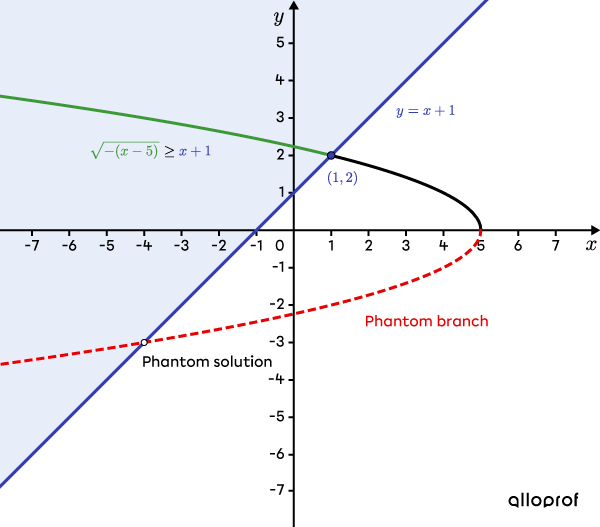
Solve the inequality |\sqrt{-(x-5)}\ge x+1.|

1. Replace the inequality symbol with the equal symbol
   ||\sqrt{-(x-5})=x+1||

2. Isolate the square root
   The square root is already isolated.

3. Calculate the restrictions
   In the equation, |\sqrt{-(x-5)}| is greater than or equal to |0| when the following restriction is respected.
   ||\begin{align}x+1&\ge0\\x&\ge-1\end{align}||
   For the restriction under the root, we have:
   ||\begin{align}-(x-5)&\ge0\\\color{#EC0000}{-1\times}-(x-5)&\color{#EC0000}{\le}0\color{#EC0000}{\times-1}\\x-5&\le0\\x&\le5\end{align}||

4. Square both sides of the equation
   ||\begin{align}\sqrt{-(x-5)}&=x+1\\\color{#EC0000}{\left(\color{black}{\sqrt{-(x-5)}}\right)^2}&=\color{#EC0000}{\left(\color{black}{x+1}\right)^2}\end{align}||

5. Solve the equation
   First, transform the equation so it is equal to |0| and then use the quadratic formula.
   ||\begin{align}-(x-5)&=x^2+2x+1\\-x+5&=x^2+2x+1\\0&=x^2+3x-4\\\\x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\x&=\dfrac{-(3)\pm\sqrt{(3)^2-4(1)(-4)}}{2(1)}\\\\x&=\dfrac{-3\pm\sqrt{25}}{2}\\\\x&\in\{-4,1\}\end{align}||

6. Verify the solutions of the equation
   The value |x=-4| is not valid, because it does not respect the restriction |x\ge-1| calculated in step 3. However, the value |x=1| is valid, because it respects both the restrictions |x\ge-1| and |x\le5.|

7. Determine the solution set of the inequality
   To determine the solution set, sketch the graph of the square root function |f(x)=\sqrt{-(x-5)}.| Here's how.