The inverse of an absolute value function is comprised of 2 rays that stem from the same point and form a sideways V. The domain of these 2 rays is the range of the original absolute value function.
Be careful! The inverse of an absolute value function is not a function, because for one |x| value there are 2 different |y| values.

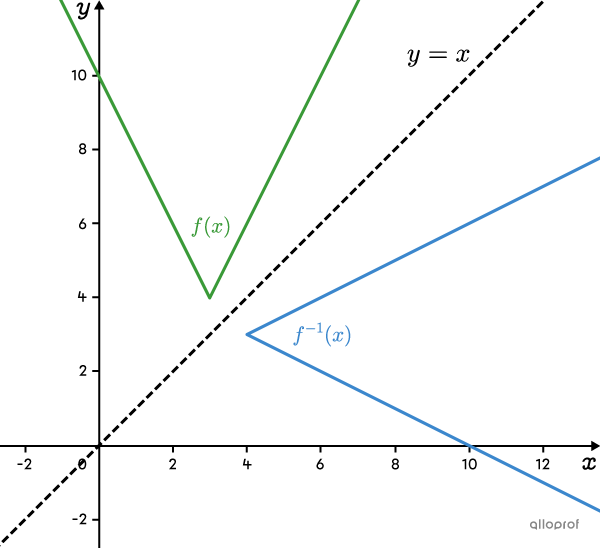
If the absolute value function opens upwards (when |a| is positive), its inverse opens to the right. In this case, |\text{range}(\color{#3a9a38}{f})=[k,+\infty[\;=\text{dom}(\color{#3b87cd}{f^{-1}}).|
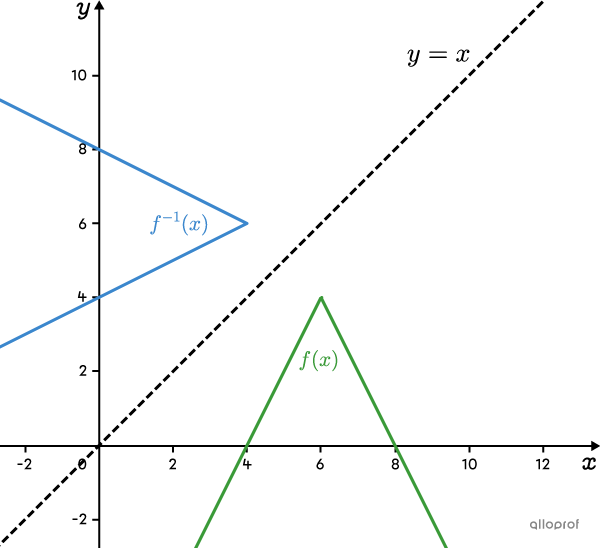
If the absolute value function opens downwards (when |a| is negative), its inverse opens to the left. In this case, |\text{range}(\color{#3a9a38}{f})=]-\infty,k]=\text{dom}(\color{#3b87cd}{f^{-1}}).|
Here are the steps to find the inverse of an absolute value function.
-
Switch |x| and |y.|
-
Isolate |y| to form 2 first degree equations.
-
Determine the domain of the inverse.
Find the rule for the inverse of the following function: |f(x).| ||f(x)=2\vert x-8\vert +2||
-
Switch |\boldsymbol{x}| and |\boldsymbol{y}|||\begin{align} \color{#3b87cd}{y}&=2\vert \color{#ff55c3}{x}-8\vert +2\\ \color{#ff55c3}{x}&=2\vert \color{#3b87cd}{y}-8\vert +2 \end{align}||
-
Isolate |\boldsymbol{y}| to form 2 first degree equations
Use the same approach as when we solve an equation containing an absolute value. First, isolate the absolute value bracket |\vert \color{#3b87cd}{y}-8\vert.| Next, apply the definition of the absolute value to form 2 equations, and then isolate |\color{#3b87cd}{y}| in each of these equations.||\begin{gather}\begin{aligned}x-2&=2\vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x-2}{2} &= \vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x}{2}-1 &= \vert \color{#3b87cd}{y}-8\vert \end{aligned}\\\Updownarrow\\ \overbrace{
\begin{aligned}
\dfrac{x}{2}-1&=\color{#3b87cd}{y}-8&\color{#ec0000}-\left(\dfrac{x}{2}-1\right)&=\color{#3b87cd}{y}-8\\
\dfrac{x}{2}+7&=\color{#333fb1}{y_1}&-\dfrac{x}{2}+1&=\color{#3b87cd}{y}-8\\
&&-\dfrac{x}{2}+9&=\color{#51b6c2}{y_2}
\end{aligned}} \end{gather}||So, the inverse of the absolute value function is 2 linear functions: |\color{#333fb1}{y_1}| and |\color{#51b6c2}{y_2}.|
The domain of these 2 lines must now be restricted to only contain the rays forming a V that opens to the correct side.
-
Determine the domain of the inverse
To do this, first determine the coordinates of the vertex of the original function and those of its inverse.
The vertex of |f(x)| is located at the point |(h,k)=(8,2).| To find the vertex of the inverse |f^{-1}(x),| swap the coordinates. This means the vertex of |f^{-1}(x)| is |(2,8).|
Since parameter |a| of |f(x)| is positive, the function opens upwards. So, the range of |f(x)| has the form |[k,+\infty[.| ||\text{range}(f)=[2,+\infty[.|| The range of |f(x)| becomes the domain of |f^{-1}(x).| ||\text{dom}(f^{-1})=[2,+\infty[.|| So, the inverse opens to the right.
Answer: The inverse of |\color{#3a9a38}{f(x)=2\vert x-8\vert +2}| has 2 rays: |\color{#333fb1}{y_1=\dfrac{x}{2}+7}| and |\color{#51b6c2}{y_2 = -\dfrac{x}{2}+9}| where |x\geq2.|
Here is the graph that shows|\color{#3a9a38}{f(x)}| as well as the two |(\color{#333fb1}{y_1}| and |\color{#51b6c2}{y_2})| rays that form its inverse.
Note: |f(x)| and its inverse are symmetric with respect to the axis |y=x.|

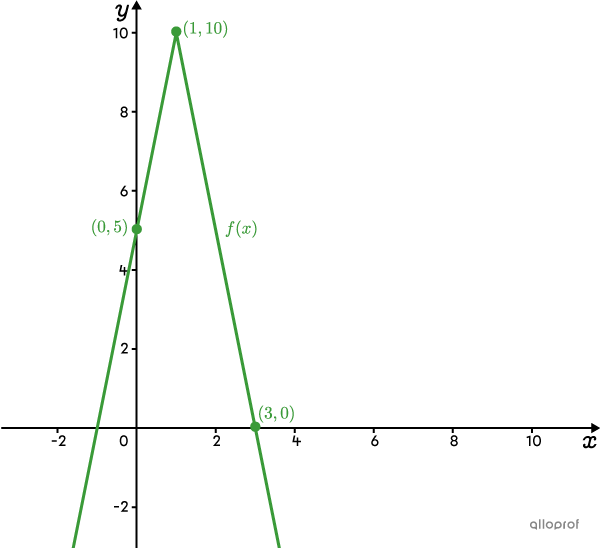
It is possible to graph the inverse of a function by swapping the |x| and |y| coordinates of some points. For example, here is the absolute value function |\color{#3a9a38}{f(x)}| graphed on the Cartesian plane.
-
The vertex of |\color{#3a9a38}{f(x)}| becomes the vertex of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(1,10)}\ \rightarrow\ \color{#3b87cd}{(10,1)}||
-
The y-intercept of |\color{#3a9a38}{f(x)}| becomes a zero of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(0,5)}\ \rightarrow\ \color{#3b87cd}{(5,0)}||
-
A zero of |\color{#3a9a38}{f(x)}| becomes the initial y-intercept of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(3,0)}\ \rightarrow\ \color{#3b87cd}{(0,3)}.||
Since we now have the vertex and a point on each branch of the inverse, it is possible to graph |\color{#3b87cd}{f^{-1}(x)}.|
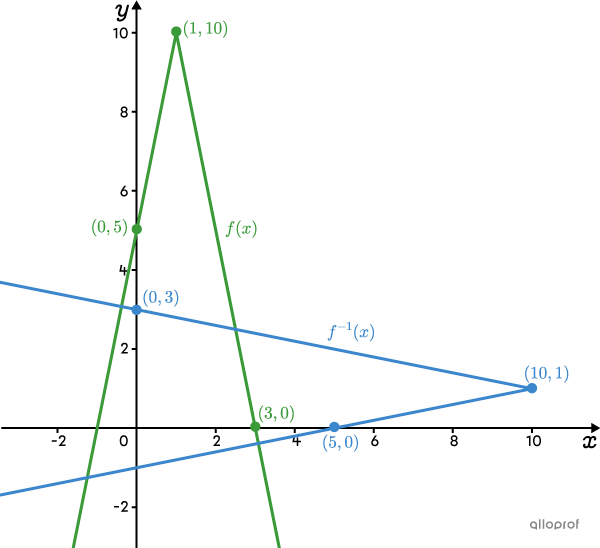
The rule of the 2 linear functions can also be found using 2 points.
-
The top branch gives the rule |y_1=-\dfrac{x}{5}+3| where |x\leq 10.|
-
The bottom branch gives the rule |y_2=\dfrac{x}{5}-1| where |x\leq 10.|