Content code
m1265
Slug (identifier)
minimum-conditions-of-congruence-of-triangles
Parent content
Similarity, Congruence, and Equivalence
Grades
Secondary IV
Topic
Mathematics
Tags
congruent triangles
minimum conditions of congruency
Content
Contenu
Corps

When comparing polygons, we can determine if they are congruent (isometric) figures by checking if they have congruent corresponding angles and sides. The same is true for triangles. Fortunately, to prove that two triangles are congruent, it is not necessary to know the measure of all the sides and angles. It is enough to check that certain minimal conditions are met. These are called the minimum conditions for congruent triangles.

Content
Corps

The minimal conditions for congruent triangles allow us to prove that triangles are congruent using the fewest possible pieces of information.

Corps

There are 3 minimal conditions to prove the congruence of triangles. There are also minimal conditions for proving the similarity of triangles. We use the most appropriate condition depending on the information provided in the problem and we organize our argument in a table of statements and justifications.

Links
Type
Anchor
Title
SSS: Side-Side-Side
Anchor
side-side-side
Internal link
/en/students/vl/mathematics/minimum-conditions-of-congruence-of-triangles-m1265
Type
Anchor
Title
SAS: Side-Angle-Side
Anchor
side-angle-side
Internal link
/en/students/vl/mathematics/minimum-conditions-of-congruence-of-triangles-m1265
Type
Anchor
Title
ASA: Angle-Side-Angle
Anchor
angle-side-angle
Internal link
/en/students/vl/mathematics/minimum-conditions-of-congruence-of-triangles-m1265
Type
Anchor
Title
Solving Problems Using the Minimal Conditions of Congruence (Isometry)
Anchor
problems
Title (level 2)
The 3 Minimal Conditions for Congruent Triangles
Title slug (identifier)
minimal-conditions-congruent-triangles
Contenu
Corps

We can explain why the minimal conditions are sufficient to assert that triangles are congruent (isometric) by examining the construction of the triangles in question.

Video
Cas de congruence des triangles
Title (level 3)
SSS : Side-Side-Side
Title slug (identifier)
side-side-side
Content
Corps

Triangles are congruent (isometric) if and only if their corresponding sides are congruent.

Corps

The condition SSS (Side-Side-Side) does not involve any angle measure. In fact, it is enough to know that the 3 pairs of corresponding sides have the same measure to conclude that the triangles are congruent.

Content
Corps

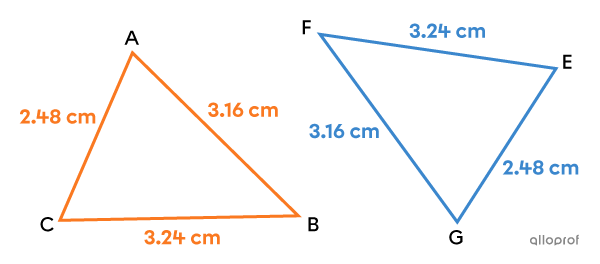
Prove that the following triangles |ABC| and |GFE| are congruent.

Image
Triangles ABC and EFG are congruent since their corresponding sides are identical.
Corps
Statement Justification

1

Segments |\overline{AC}| and |\overline{EG}| are congruent.
||\overline{AC} \cong\overline{EG}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{AC}=\text{m}\overline{EG}=2.48\ \text{cm}.|

2

Segments |\overline{AB}| and |\overline{FG}| are congruent.
||\overline{AB} \cong\overline{FG}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{AB}=\text{m}\overline{FG}=3.16\ \text{cm}.|

3

Segments |\overline{BC}| and |\overline{EF}| are congruent.
||\overline{BC} \cong \overline{EF}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{BC} = \text{m}\overline{EF}=3.24\ \text{cm}.|

4

Triangles |ABC| and |GFE| are congruent.
||\triangle ABC \cong \triangle GFE||

They satisfy the minimal condition SSS: triangles are congruent if and only if their corresponding sides are congruent.
Content
Corps

Before starting a proof of congruence (isometry), it is important to identify the pairs of corresponding sides. In the previous example, the 2 triangles are associated by a rotation. The segments |\overline{AC}| and |\overline{GE}| are corresponding, because each segment is the smallest side of its triangle. We apply the same reasoning for the 2 other pairs of corresponding sides.

Title (level 3)
SAS : Side-Angle-Side
Title slug (identifier)
side-angle-side
Content
Corps

Triangles are congruent (isometric) if and only if they have a pair of congruent angles located between 2 pairs of corresponding congruent sides.

Content
Corps

Prove that the following triangles |ABC| and |GFE| are congruent.

Image
Triangles ABC and GEF are congruent since they have a congruent angle located between 2 corresponding congruent sides.
Corps
Statement Justification

1

Segments |\overline{AB}| and |\overline{FG}| are congruent.
||\overline{AB} \cong\overline{FG}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{AB} = \text{m}\overline{FG}=2.72\ \text{cm}.|

2

Angles |ABC| and |GFE| are congruent.
||\angle{ABC} \cong \angle{GFE}||

A

By hypothesis.
The information is given on the figures.
|\text{m}\angle{ABC}=\text{m}\angle{GFE}=83.2^\circ.|

3

Segments |\overline{BC}| and |\overline{EF}| are congruent.
||\overline{BC} \cong \overline{EF}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{BC}=\text{m}\overline{EF}=3.50\ \text{cm}.|

4

Triangles |ABC| and |GFE| are congruent
||\triangle ABC \cong \triangle GFE||

They satisfy the minimal condition SAS: triangles are congruent if and only if they have a pair of congruent angles located between 2 pairs of corresponding congruent sides.
Content
Corps

The chosen angle must be formed by the corresponding pairs of congruent sides. If the angle is not in the right place, the 2 triangles are not necessarily congruent.

Image
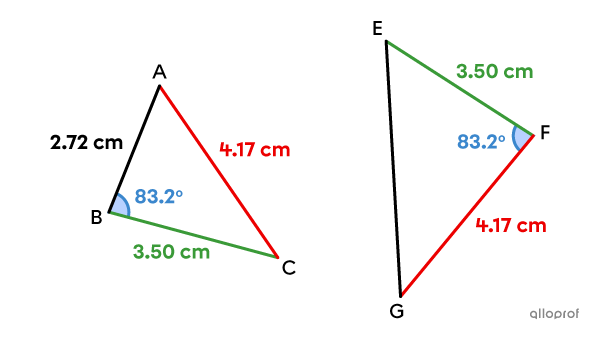
These 2 triangles do not respect the minimal condition SAS, so they are not congruent.
Corps

For example, in the image above, |\angle{ABC}| and |\angle{EFG}| have the same measure. However, angle |ABC| is located between the sides measuring |2.72| and |3.50\ \text{cm},| whereas angle |EFG| is located between the sides measuring |4.17| and |3.50\ \text{cm}.| Therefore, the 2 triangles are not congruent.
||\triangle ABC\color{#ec0000}\not\cong\triangle EFG||

Title (level 3)
ASA : Angle-Side-Angle
Title slug (identifier)
angle-side-angle
Content
Corps

Triangles are congruent (isometric) if and only if they have a pair of congruent sides located between 2 pairs of corresponding congruent angles.

Content
Corps

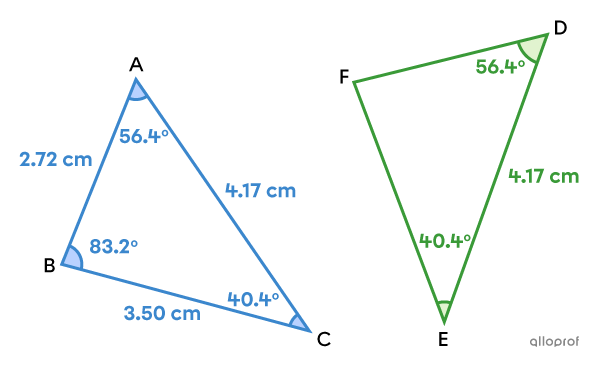
Prove that the following triangles |ABC| and |DFE| are congruent.

Image
Triangle DEF is congruent to triangle ABC, since it has one congruent side located between 2 corresponding congruent angles.
Corps
Statement Justification

1

Angles |BAC| and |EDF| are congruent.
||\angle{BAC} \cong \angle{EDF}||

A

By hypothesis.
The information is given on the figures.
|\text{m}\angle{BAC}=\text{m}\angle{FDE}=56.4^\circ.|

2

Segments |\overline{AC}| and |\overline{DE}| are congruent.
||\overline{AC} \cong \overline{DE}||

S

By hypothesis.
The information is given on the figures.
|\text{m}\overline{AC}=\text{m}\overline{DE}=4.17\ \text{cm}.|

3

Angles |ACB| and |DEF| are congruent.
||\angle{ACB} \cong \angle{DEF}||

A

By hypothesis.
The information is given on the figures.
|\text{m}\angle{ACB}=\text{m}\angle{DEF}=40.4^\circ.|

4

Triangles |ABC| and |DEF| are congruent.
||\triangle ABC \cong \triangle DEF||

They satisfy the minimal condition ASA: triangles are congruent if and only if they have one pair of congruent sides located between 2 pairs of corresponding congruent angles.
Content
Corps

The location of the pairs of corresponding sides and angles in the triangles is critical. If the pair of corresponding sides is not located between the 2 pairs of corresponding angles, then the 2 triangles are not necessarily congruent (isometric).

Image
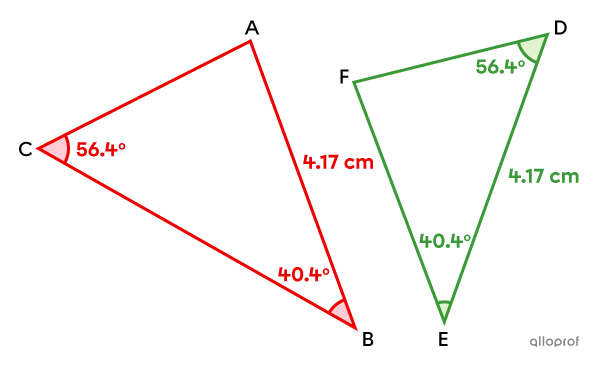
The 2 triangles do not meet the minimum condition ACA, so they are not congruent.
Corps

For example, in triangle |ABC,| the side that measures |4.17\ \text{cm}| is not located between the angles of |40.4^\circ| and |56.4^\circ,| while it is in triangle |DEF.| The triangles |ABC| and |DEF| are therefore not congruent.
||\triangle ABC\color{#ec0000}\not\cong\triangle DEF||

Title (level 2)
Solving Problems Using the Minimal Conditions of Congruence (Isometry)
Title slug (identifier)
problems
Contenu
Corps

It is possible to use the minimal conditions for congruence of triangles as well as the properties of quadrilaterals to construct proofs.

Content
Columns number
2 columns
Format
50% / 50%
First column
Corps

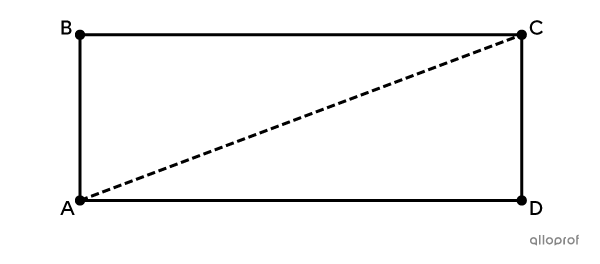
The following quadrilateral |ABCD| is a rectangle.

Prove that the triangles |ABC| and |CDA| are congruent.

Second column
Image
A rectangle with a diagonal.
Solution
Corps
Statement Justification

1

Segments |\overline{AB}| and |\overline{CD}| are congruent.
||\overline{AB} \cong \overline{CD}||

S

The opposite sides of a rectangle are congruent.

2

Angles |ABC| and |CDA| are congruent.
||\angle{ABC} \cong \angle{CDA}||

A

The angles of a rectangle are right angles.

3

Segments |\overline{BC}| and |\overline{AD}| are congruent.
||\overline{BC} \cong \overline{AD}||

S

The opposite sides of a rectangle are congruent.

4

Triangles |ABC| and |CDA| are congruent.
||\triangle ABC \cong \triangle CDA||

They satisfy the minimal condition SAS: triangles are congruent if and only if they have a pair of congruent angles located between 2 pairs of corresponding congruent sides.
Content
Columns number
2 columns
Format
50% / 50%
First column
Corps

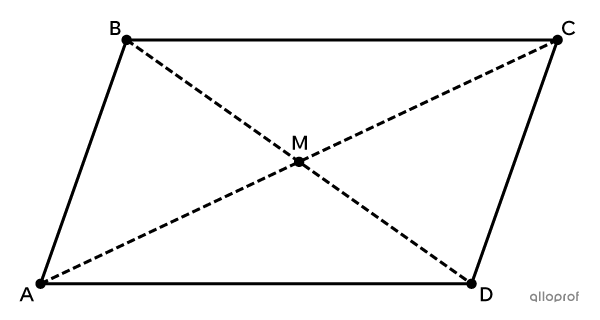
The following quadrilateral |ABCD| is a parallelogram. |M| is the intersection point of the 2 diagonals |\overline{BD}| and |\overline{AC}.|

Prove that the triangles |BCM| and |DAM| are congruent.

Second column
Image
A parallelogram with its 2 diagonals.
Solution
Corps
Statement Justification

1

Segments |\overline{BC}| and |\overline{AD}| are congruent.
||\overline{BC} \cong\overline{AD}||

S

The opposite sides of a parallelogram are congruent.

2

Segments |\overline{BM}| and |\overline{DM}| are congruent.
||\overline{BM} \cong \overline{DM}||

S

The diagonals of a parallelogram bisect each other (that is, they intersect at their midpoints).

3

Segments |\overline{AM}| and |\overline{CM}| are congruent.
||\overline{AM} \cong \overline{CM}||

S

The diagonals of a parallelogram bisect each other  (that is, they intersect at their midpoints).

4

Triangles |BCM| and |DAM| are congruent.
||\triangle BCM \cong \triangle DAM||

They satisfy the minimal condition SSS: triangles are congruent if and only if their corresponding sides are congruent.
Corps

After having proved that triangles are congruent, we can find missing measurements of either of the triangles. Here is an example where we use the minimal conditions to find a missing measurement.

Content
Corps

We must first prove that the triangles are congruent using the information provided in the problem before calculating missing measurements.

Content
Columns number
2 columns
Format
50% / 50%
First column
Corps

Find the measure of |\overline{AD}| given that |\overline{AC}| is the bisector of angle |DAB.|

Second column
Image
The measure of one side of triangle ACD is sought.
Solution
Corps
Statement Justification

1

Angles |DAC| and |BAC| are congruent.
||\angle{DAC} \cong \angle{BAC}||

A

|\overline{AC}| is the bisector of angle |DAB.|
||\text{m}\angle{DAC} = \text{m}\angle{BAC}=\dfrac{156^\circ}{2}=78^\circ||

2

Segments |\overline{CA}| and |\overline{CA}| are congruent.
||\overline{CA} \cong \overline{CA}||

S

It is a common side to both triangles.

3

Angles |ACB| and |ACD| are congruent.
||\angle{ACB} \cong \angle{ACD}||

A

Since the sum of the interior angles of a triangle is |180^\circ,| we find that |\text{m}\angle{ACB}=63^\circ.|
||\begin{align}\text{m}\angle{ACB}&=180^\circ-78^\circ-39^\circ\\&=63^\circ\\&=\text{m}\angle{ACD}\end{align}||

4

Triangles |ADC| and |ABC| are congruent.
||\triangle ADC \cong \triangle ABC||

They satisfy the minimal condition ASA: triangles are congruent if and only if they have one pair of congruent sides located between 2 pairs of corresponding congruent angles.

5

|\text{m}\overline{AD} =6\ \text{cm}|

Corresponding sides of congruent triangles are congruent. Therefore, ||\text{m}\overline{AD}=\text{m}\overline{AB}=6\ \text{cm}.||
Corps

Here is an example where we use the minimal conditions of congruence to complete a proof.

Content
Columns number
2 columns
Format
50% / 50%
First column
Corps

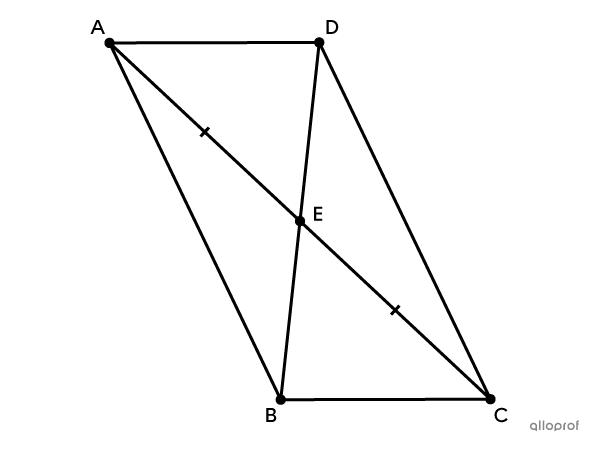
In the following figure |ABCD,| |\overline{AD}| and |\overline{BC}| are parallel and |E| is the midpoint of |\overline{AC}.|

Prove that the quadrilateral |ABCD| is a parallelogram.

Second column
Image
A quadrilateral with its 2 diagonals.
Solution
Corps
Statement Justification

1

Angles |DEA| and |BEC| are congruent.
||\angle{DEA} \cong \angle{BEC}||

A

They are vertically opposite angles.

2

Segments |\overline{AE}| and |\overline{CE}| are congruent.
||\overline{AE} \cong \overline{CE}||

S

|E| is the midpoint of |\overline{AC}.|

3

Angles |EAD| and |ECB| are congruent.
||\angle{EAD} \cong \angle{ECB}||

A

Alternate-interior angles formed by 2 parallel lines |(\overline{AD}| and |\overline{BC})| and a transversal |(\overline{AC})| are congruent.

4

Triangles |DEA| and |BEC| are congruent.
||\triangle DEA \cong \triangle BEC||

They satisfy the minimal condition ASA: triangles are congruent if and only if they have one pair of congruent sides located between 2 pairs of corresponding congruent angles.

5

Segments |\overline{BE}| and |\overline{DE}| are congruent.
||\overline{BE} \cong \overline{DE}||

Corresponding sides of congruent triangles are congruent.

6

|E| is the midpoint of |\overline{BD}.|

Since the measure of |\overline{BE}| is equal to the measure of |\overline{DE},| |E| is the midpoint of |\overline{BD}.|

7

|ABCD| is a parallelogram.

Since |E| is the midpoint of |\overline{AC}| and |\overline{BD},| and the diagonals of a parallelogram bisect each other, we can deduce that |ABCD| is a parallelogram.
Contenu
Corps

Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante.

MiniRécup Mathématiques
Title (level 2)
Exercise
Title slug (identifier)
exercise
Contenu
Contenu
Exercice
Minimum Conditions of Congruence of Triangles
Title (level 2)
See also
Title slug (identifier)
see-also
Contenu
Links
Type
Internal
Title
Minimum Conditions of Congruence of Triangles
Internal link
/en/students/vl/mathematics/minimum-conditions-of-congruence-of-triangles-m1265
Type
Internal
Title
Congruent and Similar Figures
Internal link
/en/students/vl/mathematics/congruent-and-similar-figures-m1262
Type
Internal
Title
Triangles
Internal link
/en/students/vl/mathematics/triangles-m1200
Remove audio playback
No