<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Un <strong>nombre </strong>est un concept mathématique servant à compter, évaluer, mesurer, comparer ou ordonner des grandeurs.<br>
<br>
On exprime les nombres à l'aide de caractères appelés <a href="/fr/eleves/bv/mathematiques/les-chiffres-m1013">chiffres</a>.</p>
</body></html>
Un peu comme les mots composés de lettres de l'alphabet, les nombres sont formés par la combinaison de chiffres. Il importe de bien connaitre les règles d'accord et d'écriture des nombres lorsque l'on travaille avec ceux-ci. Les nombres nous permettent d'exprimer de façon mathématique la grandeur des choses qui nous entourent.
Le nombre |6| représente le nombre d'étoiles contenues dans l'ensemble.

Le nombre |\text{-}2| est représenté par la position du point |A| sur la droite numérique.

Le nombre |72{,}95| représente le cout en dollars de cette paire de souliers.
Les nombres peuvent être ordonnés selon un ordre croissant ou décroissant, mais peuvent aussi être classés en ensembles selon leurs caractéristiques.
En fonction de leurs caractéristiques, les nombres sont classés en différents ensembles. Le schéma ci-dessous illustre les relations qui existent entre ceux-ci.
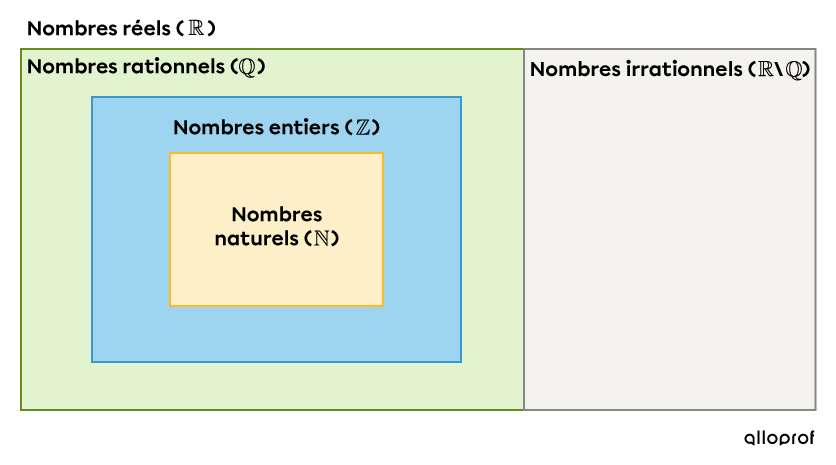
Comme on peut le voir dans ce schéma, l’ensemble des nombres naturels est inclus dans celui des nombres entiers. L’ensemble des nombres entiers est à son tour inclus dans celui des nombres rationnels. L’ensemble des nombres réels, quant à lui, est composé de l’union des ensembles des nombres rationnels et des nombres irrationnels. Le tableau suivant donne un aperçu des différents ensembles.
|
Ensemble de nombres |
Description |
Exemples |
|---|---|---|
|
Nombres naturels |
Nombres qui servent à compter |\mathbb{N} = \{0,1,2,3,4,5,\ldots\}| |
|3,\ ||5,\ ||134,\ ||2\ 099| |
|
Nombres entiers |
Nombres naturels et leurs opposés |\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots\}| |
|-133,\ ||-9,\ ||0,\ ||9,\ ||915| |
|
Nombres rationnels |
Nombres pouvant s’exprimer comme le quotient de 2 nombres entiers |
|-5{,}\overline{3},\ ||-\dfrac{1}{3},\ ||\dfrac{3}{4},\ ||3,\ ||6{,}4| |
|
Nombres irrationnels |
Nombres ne pouvant pas s’exprimer comme le quotient de 2 nombres entiers |
|\sqrt{2},\ ||\sqrt[3]{11},\ ||e,\ ||\pi| |
|
Nombres réels |
Nombres appartenant à l’ensemble des nombres rationnels ou à l’ensemble des nombres irrationnels |\mathbb{R} =\ ]{-}\infty,+\infty[| |
|-16,\ ||\dfrac{5}{8},\ ||\sqrt{5},\ ||7,\ ||23{,}\overline{6}| |
Il arrive parfois qu’on ajoute l’ensemble des nombres décimaux |(\mathbb{D})| à ces ensembles. Ce dernier regroupe tous les nombres rationnels dont le développement décimal est fini et non périodique. Il forme donc un sous-ensemble des nombres rationnels qui comprend l’ensemble des nombres entiers.
Certains symboles sont couramment utilisés pour la notation des ensembles de nombres. La tableau suivant résume la liste de ces symboles.
|
Symbole |
Définition |
Exemple |
|---|---|---|
|
|\{\ ,\,\}| |
Énumération des éléments d’un ensemble sous forme d’extension |
|\{0,1,2,3,4,...\}| |
|
|\in| |
« … appartient à… », « … est élément de… » |
|3\in \mathbb{N}| |
|
|\notin| |
« … n’appartient pas à… », « … n’est pas élément de… » |
|\dfrac{2}{5}\notin \mathbb{Z}| |
|
|\subset| |
« … est inclus dans… » |
|\mathbb{Z}\subset\mathbb{Q}| |
|
|\large\cup| |
Union de 2 ensembles |
|\mathbb{R}=\mathbb{Q} \cup \mathbb{Q’}| |
|
|\tiny\boxed{\phantom{\normalsize{t}}}^{\large*}| |
Exclusion du nombre zéro |
|\mathbb{N}^*| représente l’ensemble des nombres naturels sans |0.| |
|
|\tiny\boxed{\phantom{\normalsize{t}}}_{\large+}| |
Éléments positifs de l’ensemble seulement |
|\mathbb{Z}_+| représente l’ensemble des entiers positifs. |
|
|\tiny\boxed{\phantom{\normalsize{t}}}_{\large-}| |
Éléments négatifs de l’ensemble seulement |
|\mathbb{Q}_-| représente l’ensemble des nombres rationnels négatifs seulement. |