The parabola is one of the conics. It is obtained by the intersection of a conical surface and a plane.
A parabola is the geometric locus of all points located at equal distance from a fixed line, called the directrix, and a fixed point, called the focus.
-
Parabolas have a focus, |F.|
-
Parabolas have a vertex, |V.|
-
Parabolas have a line called the directrix.
-
The line perpendicular to the directrix, passing through the focus and the vertex, is the axis of symmetry.
-
Vertex |V| is equidistant from the focus |F| and the directrix.
Vertical parabola
A parabola is vertical when its axis of symmetry is vertical.
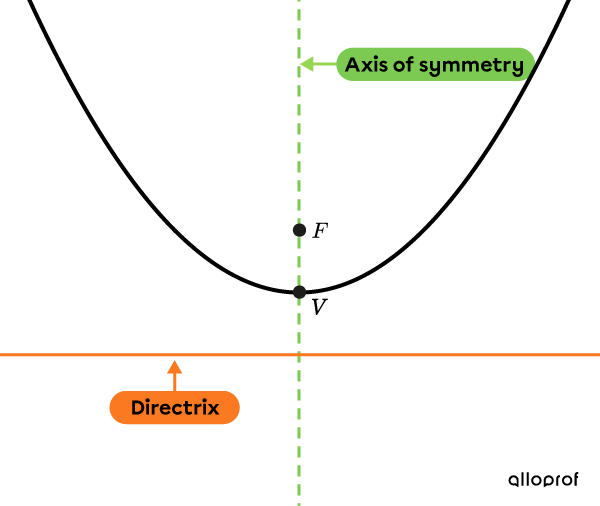
Horizontal parabola
A parabola is horizontal when its axis of symmetry is horizontal.
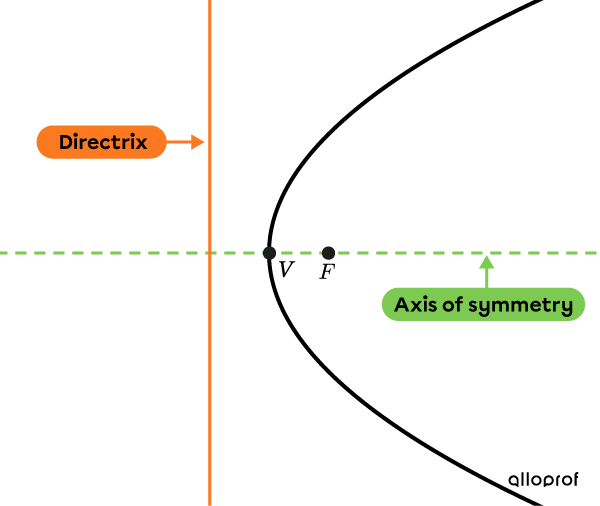
The equation that defines a parabola centred at the origin uses parameter |c.| Depending on its orientation, there are two different equations.
Vertical parabola
||x^2=4cy||Equation of the directrix: ||y=-c||
Horizontal parabola
||y^2=4cx||Equation of the directrix: ||x=-c||
where
|\vert c \vert :| distance between the vertex and the focus or between the vertex and the directrix
In the equation for a vertical parabola |x| is squared, while |y| is squared in the equation for a horizontal parabola equation.
The latus rectum is a line segment that passes through the focus of a parabola and is perpendicular to its axis of symmetry. The length of a parabola’s latus rectum is |4c.| The latus rectum determines the opening of the parabola at the focus.
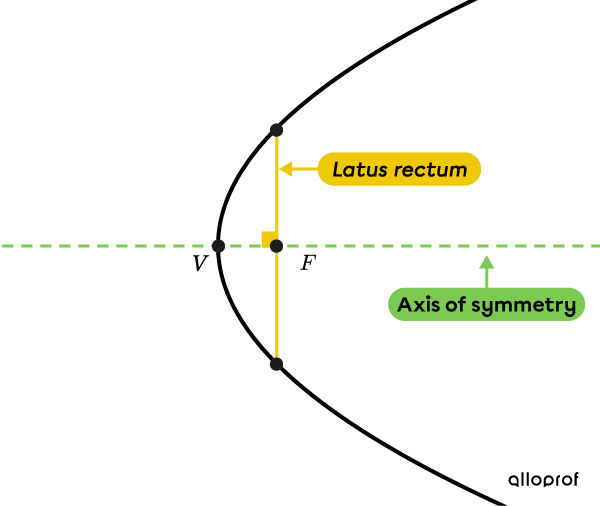
Here are the graphic representations of the two types of parabolas with the placement of important points and their coordinates.
Vertical parabola
If |c>0,| the parabola opens upwards.
If |c<0,| the parabola opens downwards.

Horizontal parabola
If |c>0,| the parabola opens to the right.
If |c<0,| the parabola opens to the left.
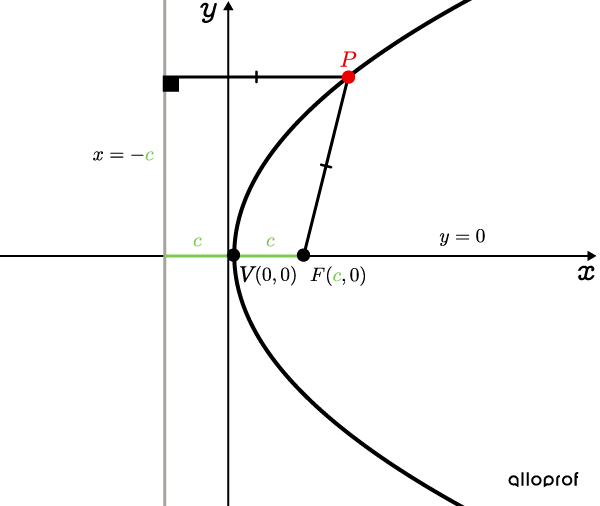
All |\color{#EC0000}P| points are equidistant from the directrix and focus |F.|
To determine the equation of a parabola centred at the origin, first find the value of parameter |c.|
-
Based on the parabola’s orientation, determine the sign of parameter |\color{#3a9a38}c| and the equation to use.
-
Determine the value of parameter |\color{#3a9a38}c| using one of the following strategies:
a) If the equation of the directrix is given, find the value of |\color{#3a9a38}c.|
b) If the coordinates of the focus are provided, find the value of |\color{#3a9a38}c.|
c) If a point on the parabola is given, substitute its coordinates into the parabola’s equation.
-
Write the parabola’s equation.
Here is an example where the equation of the directrix is provided.
Determine the equation of the following parabola.

-
Determine the sign of parameter |c| as well as the equation to use
The parabola is horizontal and opens to the right. Therefore, parameter |c| is positive and the equation is:||y^2=4cx|| -
Determine the value of parameter |c|
Since the directrix equation is |x=-10,| it means that |\color{#3a9a38}{c}=\color{#3a9a38}{10}.| -
Write the equation of the parabola
Replacing the value of the parameters gives the following: ||\begin{align}y^2&=4\color{#3a9a38}cx\\y^2&=4(\color{#3a9a38}{10})x\\ y^2&=40x\end{align}||
-
Determine the parabola’s orientation.
-
Use parameter |\color{#3a9a38}{c}| to determine the coordinates of the focus and the equation of the directrix.
-
Find other points on the parabola using the equation.
-
Draw the parabola and its directrix.
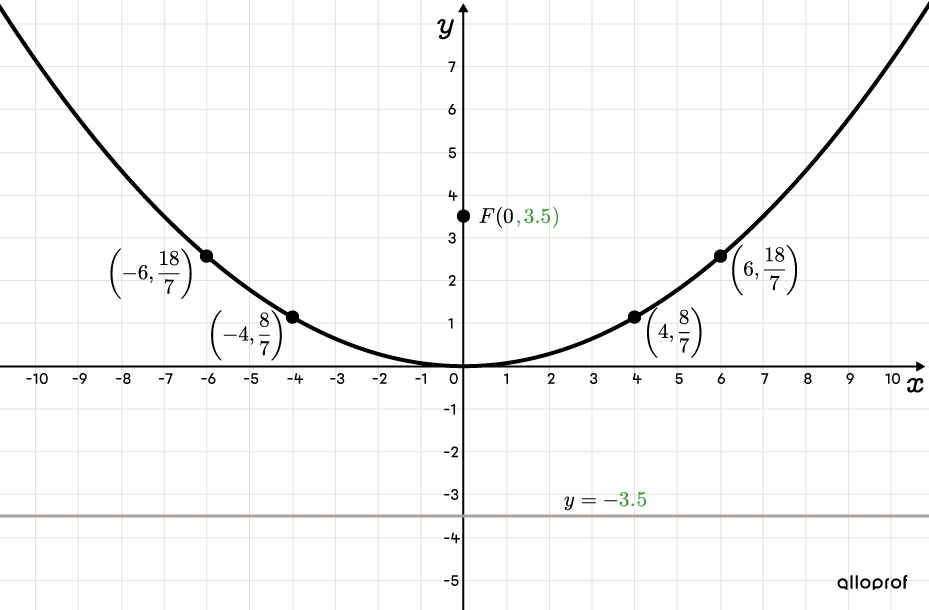
Sketch the parabola whose equation is |x^2=14y.|
-
Determine the parabola’s orientation
Since |x| is squared, the parabola is vertical. Also, parameter |c| is positive. Therefore, the parabola will open upwards. -
Determine the coordinates of the focus and the equation of the directrix||\begin{align}
4c&=14\\c&=\dfrac{14}{4}\\\color{#3a9a38}{c}&=\color{#3a9a38}{3{.}5}\end{align}|| The focus is the point |(0\ ,3{.}5)| and the equation of the directrix is: ||\begin{align}y&=-\color{#3a9a38}{c}\\y&=-\color{#3a9a38}{3{.}5}\end{align}|| -
Find other points on the parabola using the equation
If |x=4,| then: ||\begin{align}x^2&=14y\\(4)^2&=14y\\16&=14y\\\dfrac{8}{7}&=y\end{align}||
The parabola passes through point |\left(4,\dfrac{8}{7}\right).| As the parabola is symmetrical in relation to the axis |x=0,| it’s understood that it also passes through point |\left(-4,\dfrac{8}{7}\right).|
Following the same principle, it’s possible to find points |\left(6,\dfrac{18}{7}\right)| and |\left(-6,\dfrac{18}{7}\right).| -
Sketch the parabola and its directrix
Here is an animation to help you understand the different relationships and the role of parameters in the parabola.
The equation that defines the parabola not centred at the origin uses parameters |c,| |h,| and |k.| As with the parabola centred at the origin, there are two different equations depending on its orientation.
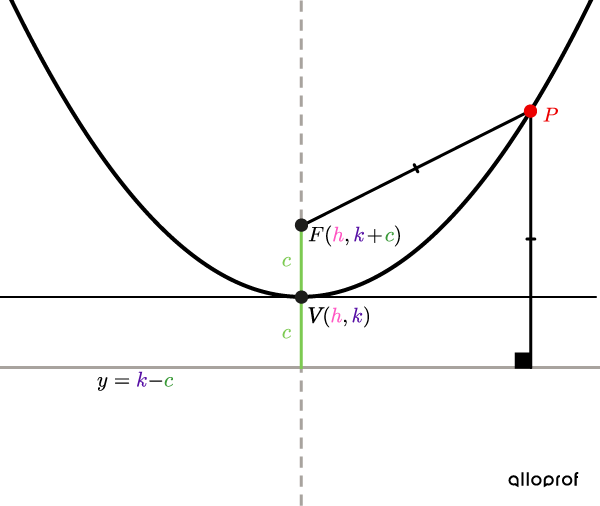
Vertical parabola
||(x-h)^2=4c(y-k)|| Equation of the directrix:||y=k-c||
Horizontal parabola
||(y-k)^2=4c(x-h)|| Equation of the directrix:||x=h-c||
where
|\vert c \vert:| distance between the vertex and the focus or between the vertex and the directrix
|(h,k):| coordinates of the parabola’s vertex
Here are graphic representations of the two types of parabolas with the placement of important points and their coordinates.
Vertical parabola
If |c>0,| the parabola opens upwards.
If |c<0,| the parabola opens downwards.
Horizontal parabola
If |c>0,| the parabola opens to the right.
If |c<0,| the parabola opens to the left.
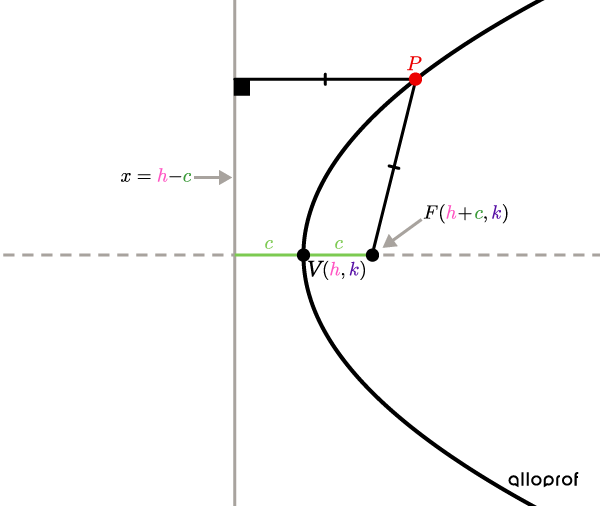
All points |\color{#EC0000}P| are equidistant from the directrix and focus |F.|
To determine the equation of a parabola not centered at the origin, it is necessary to find the value of parameters |c,| |h,| and |k.|
-
Use the orientation of the parabola to determine the sign of parameter |\color{#3a9a38}c| and the equation.
-
Determine the value of parameters |\color{#3a9a38}c,| |\color{#FF55C3}h,| and |\color{#560FA5}k.| If one or more of these parameters are missing, use one of the following strategies:
a) If the vertex and the equation of the directrix are provided, determine parameter |\color{#3a9a38}c| by substituting the information into the equation of the directrix.
b) If the vertex and a point belonging to the parabola are provided, determine parameter |\color{#3a9a38}c| by substituting the information into the parabola’s equation.
c) If the coordinates of the focus and the equation of the directrix are provided, deduce the missing parameters using the parabola’s properties.
-
Write the parabola’s equation.
Here is an example where the equation of the directrix and the coordinates of the focus are given.
Determine the equation of the following parabola.
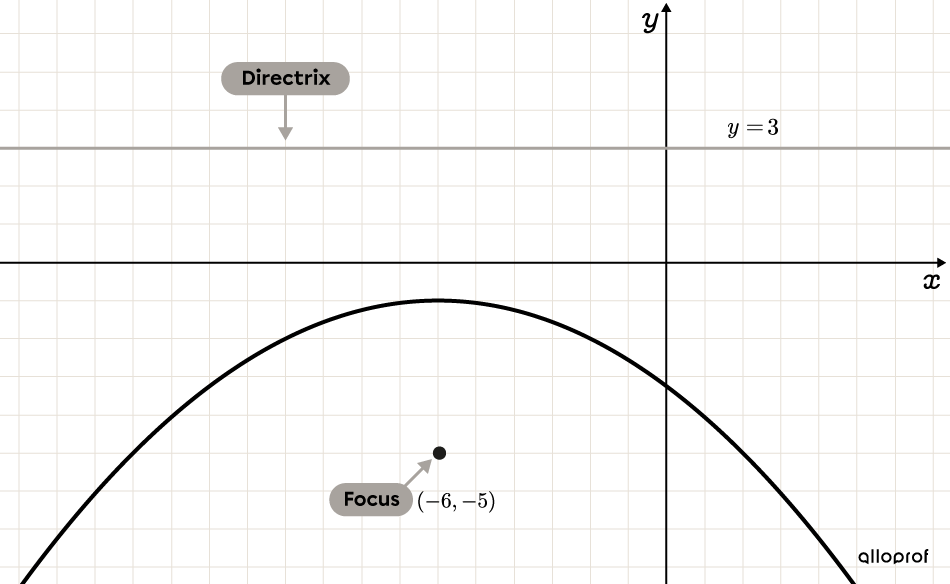
-
Determine the sign of parameter |c| and the equation to use
Since the parabola is vertical and opens downward, |\color{#3a9a38}c| is negative. Use the following equation:||(x-h)^2=4c(y-k)|| -
Determine missing parameters
In this case, the three parameters used to determine the equation of the parabola are missing. Therefore, use its properties with the information provided.
We know that the distance between the focus and the vertex is equal to the distance between the directrix and the vertex. Therefore, the vertical distance between the focus and the directrix is |2\vert\color{#3a9a38}c\vert.| ||\begin{align}2\vert\color{#3a9a38}c\vert &=\vert3--5\vert \\2\vert\color{#3a9a38}c\vert &=\vert8\vert\\ \vert\color{#3a9a38}c\vert&=\color{#3a9a38}4\end{align}||
Since we know that |c| is negative, we have: ||\color{#3a9a38}c=\color{#3a9a38}{-4}|| The coordinates |(\color{#FF55C3}h,\color{#560FA5}k)| of the vertex can be found by adding the value of |\vert \color{#3a9a38}c\vert| to the y-value of the focus. ||\begin{align} (\color{#FF55C3}h,\color{#560FA5}k)&=(\color{#FF55C3}{-6},-5+\color{#3a9a38}{4})\\ &= (\color{#FF55C3}{-6},\color{#560FA5}{-1}) \end{align}||
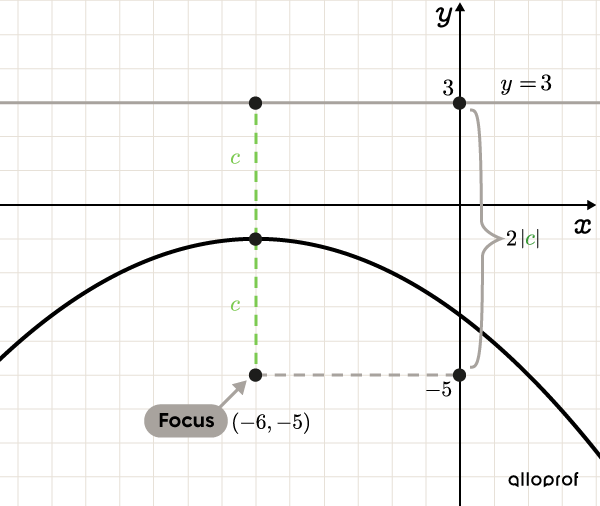
-
Write the parabola’s equation
Replacing the value of the parameters gives us the following: ||\begin{align}(x-\color{#FF55C3}h)^2&=4\color{#3a9a38}c(y-\color{#560FA5}k)\\(x-\color{#FF55C3}{-6})&=4(\color{#3a9a38}{-4})(y-\color{#560FA5}{-1})\\(x+6)^2&=-16(y+1)\end{align}||
-
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and mark the parabola’s vertex.
-
Determine the parabola’s orientation.
-
Determine the coordinates of the focus and the equation of the directrix using parameter |\color{#3a9a38}c.|
-
Use the equation to find other points on the parabola.
-
Sketch the parabola and its directrix.
Draw the parabola whose equation is |(y-1)^2=-8(x+3).|
-
Identify Parameters |h| and |k| in the equation and mark the parabola’s vertex
According to the equation, the vertex is located at the following coordinates: ||(\color{#FF55C3}h,\color{#560fa5}k)=(\color{#FF55C3}{-3},\color{#560fa5}{1})|| -
Determine the parabola’s orientation
Since it is the brackets that contains the term |y| which is squared, the parabola is horizontal. Also, parameter |c| is negative. The parabola will therefore open to the left. -
Determine the coordinates of the focus and the equation of the directrix line||\begin{align}4\color{#3a9a38}c&=-8\\\color{#3a9a38}c&=\dfrac{-8}{4}\\\color{#3a9a38}{c}&=\color{#3a9a38}{-2}\end{align}|| The focus is at the following coordinates: ||\begin{align}(\color{#FF55C3}h+\color{#3a9a38}{c}&,\color{#560fa5}k)\\(\color{#FF55C3}{-3}+\color{#3a9a38}{-2}&,\color{#560fa5}{1})\\(-5&,1)\end{align}|| The equation of the directrix is: ||\begin{align}x&=\color{#FF55C3}h-\color{#3a9a38}{c}\\x&=\color{#FF55C3}{-3}-\color{#3a9a38}{-2}\\x&=-1\end{align}||
-
Use the equation to find other points on the parabola
Since |y| is squared, it’s possible to choose a value for |y| to determine the corresponding |x|. If |y=5,| then: ||\begin{align}(y-1)^2&=-8(x+3)\\(5-1)^2&=-8(x+3)\\16&=-8(x+3)\\-2&=x+3\\-5&=x\end{align}|| The parabola passes through point |(-5,5).| Since the parabola is horizontal and its focus is at |(-5,1)| , the vertical distance between the focus and the point found is |4| units. Therefore, the y-value of its symmetrical point can be found, is also at a distance of |4| units from the focus. This gives the following point: |(-5,-3).| -
Sketch the parabola and its directrix

Apply the following properties when representing a region bounded by a parabola.
A parabola’s interior corresponds to the region where the focus is located. The signs of inequality are less than |(<)| or less than or equal to |(\leq).|
Conversely, the exterior is the region where the focus is not located. The signs are greater than |(>)| or greater than or equal to |(\geq).|
Vertical parabola |
||
|
Region of the Cartesian Plane |
Graphical Representation |
Corresponding Inequality |
|---|---|---|
|
The interior, excluding the curve |
 |
||\begin{align}x^2&<4cy\\\\ |
|
The exterior, excluding the curve |
 |
||\begin{align}x^2&>4cy\\\\ |
Horizontal parabola |
||
|
Region of the Cartesian Plane |
Graphical Representation |
Corresponding Inequality |
|
The interior, excluding the curve |
 |
||\begin{align}y^2&<4cx\\\\ |
|
The exterior, excluding the curve |
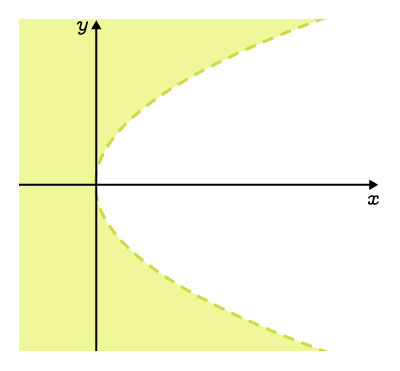 |
||\begin{align}y^2&>4cx\\\\ |
To include the points that are on the parabola, change the inequality symbols |<,>| for symbols |\leq,\geq.|