To find the intersection point(s) between a line and a conic, we solve the system of equations composed of first-degree and second-degree equations.
-
Use the substitution method to obtain an equation with one variable.
-
Manipulate the equation so it equals |0.|
-
Solve the equation to find the value(s) of the isolated variable.
-
Replace the value(s) obtained into one of the original equations to obtain the value(s) of the other variable.
-
Write the coordinates of the point(s) of intersection.
Unlike the intersection between a parabola and a conic, there are three possible cases regarding the number of solutions:
-
the line and the conic do not intersect;
-
the line and the conic intersect only at one place, called the point of tangency;
-
the line and the conic intersect at two distinct places.
In the following interactive video, select a conic and drag the cursor to study the possible cases.
-
Use the substitution method
We use the substitution method since variable |y| in the equation of the line is already isolated.||\begin{align}
x^2+\color{#3a9a38}{y}^2&=10\\
x^2+(\color{#3a9a38}{2x+5})^2&=10
\end{align}|| -
Manipulate the equation so that it equals |0|
||\begin{align}
x^2+(2x+5)^2&=10\\
x^2+(4x^2+20x+25)&=10\\
\color{#3B87CD}{5}x^2+\color{#3A9A38}{20}x+\color{#EC0000}{15}&=0
\end{align}|| -
Solve the equation
Using the quadratic formula, we obtain:||\begin{align}
x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\
&=\dfrac{-(\color{#3A9A38}{20})\pm\sqrt{(\color{#3A9A38}{20})^2-4(\color{#3B87CD}{5})(\color{#EC0000}{15})}}{2(\color{#3B87CD}{5})}\\\\
&=\dfrac{-20\pm\sqrt{100}}{10}\\\\
x_{\small{A}}&=-3\\
x_{\small{B}}&=-1
\end{align}|| -
Substitute the values obtained in one of the starting equations
For point |A| en |x_{\small{A}}=-3,| we have:||\begin{align}
y_{\small{A}}&=2\color{#3A9A38}{x_{\small{A}}}+5\\
&=2(\color{#3A9A38}{-3})+5\\
&=-1
\end{align}||As for the point |B| en |x_{\small{B}}=-1,| we have:||\begin{align}
y_{\small{B}}&=2\color{#3A9A38}{x_{\small{B}}}+5\\
&=2(\color{#3A9A38}{-1})+5\\
&=3
\end{align}|| -
Write the coordinates of the points of intersection
The coordinates of the two points of intersection between the line |y=2x+5| and the circle |x^2+y^2=10| are |A(-3,-1)| and |B(-1,3).|

-
Use substitution method
We use the substitution method since variable |y| in the equation of the line is already isolated.||\begin{align}\dfrac{x^2}{36}+\dfrac{\color{#3a9a38}{y}^2}{49}&=1\\\\ \dfrac{x^2}{36}+\dfrac{(\color{#3a9a38}{-2x+6})^2}{49}&=1\end{align}|| -
Manipulate the equation so that it equals |0|
||\begin{align}\dfrac{x^2}{36}+\dfrac{(-2x+6)^2}{49}&=1\\\\ \dfrac{49x^2}{1\ 764}+\dfrac{36(-2x+6)^2}{1\ 764}&=1\\\\ \dfrac{49x^2+36(4x^2-24x+36)}{1\ 764}&=1\\\\ 49x^2+144x^2-864x+1\ 296&=1\ 764\\ \color{#3B87CD}{193}x^2\color{#3A9A38}{-864}x\color{#EC0000}{-468}=0\end{align}|| -
Solve the equation
Using the quadratic formula, we obtain: ||\begin{align}x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\ &=\dfrac{-(\color{#3A9A38}{-864})\pm\sqrt{(\color{#3A9A38}{-864})^2-4(\color{#3B87CD}{193})(\color{#EC0000}{-468})}}{2(\color{#3B87CD}{193})}\\\\ &=\dfrac{864\pm\sqrt{1\ 107\ 792}}{386}\\\\ x_{\small{A}}&\approx-0{.}49\\ x_{\small{B}}&\approx4{.}97\end{align}|| -
Substitute the values obtained in one of the starting equations
For point |A| en |x_{\small{A}}=-0{.}49,| we have: ||\begin{align}y_{\small{A}}&=-2\color{#3A9A38}{x_{\small{A}}}+6\\ &=-2(\color{#3A9A38}{-0{.}49})+6\\ &=6{.}98\end{align}|| As for the point |B| with |x_{\small{B}}=4{.}97,| we have: ||\begin{align}y_{\small{B}}&=-2\color{#3A9A38}{x_{\small{B}}}+6\\ &=-2(\color{#3A9A38}{4{.}97})+6\\ &=-3{.}94\end{align}|| -
Write the coordinates of the points of intersection
The coordinates of the two points of intersection between the line |y=-2x+6| and the ellipse |\dfrac{x^2}{36}+\dfrac{y^2}{49}=1| are |A(-0{.}49;6{.}98)| and |B(4{.}97;-3{.}94).|

-
Use substitution method
We use the substitution method since variable |y| in the equation of the line is already isolated.||\begin{align}\dfrac{x^2}{25}-\dfrac{\color{#3a9a38}{y}^2}{100}&=1\\\\ \dfrac{x^2}{25}-\dfrac{(\color{#3a9a38}{2x-13})^2}{100}&=1\end{align}|| -
Manipulate the equation so that it equals |0|
||\begin{align}\dfrac{x^2}{25}-\dfrac{(2x-13)^2}{100}&=1\\\\ \dfrac{4x^2-(2x-13)^2}{100}&=1\\\\ 4x^2-(4x^2-52x+169)&=100\\ 52x-269&=0\end{align}|| -
Solve the equation||\begin{align}52x-269&=0\\ 52x&=269\\ x_{\small{A}}&\approx5{.}17\end{align}||
-
Substitute the value obtained in one of the starting equations
||\begin{align}y_{\small{A}}&=2\color{#3A9A38}{x_{\small{A}}}-13\\ &=2(\color{#3A9A38}{5{.}17})-13\\ &=-2{.}66\end{align}|| -
Write the coordinates of the point of intersection
The coordinates of the point of intersection between the line |y=2x-13| and the hyperbola |\dfrac{x^2}{25}-\dfrac{y^2}{100}=1| are |A(5{.}17,-2{.}66).|

-
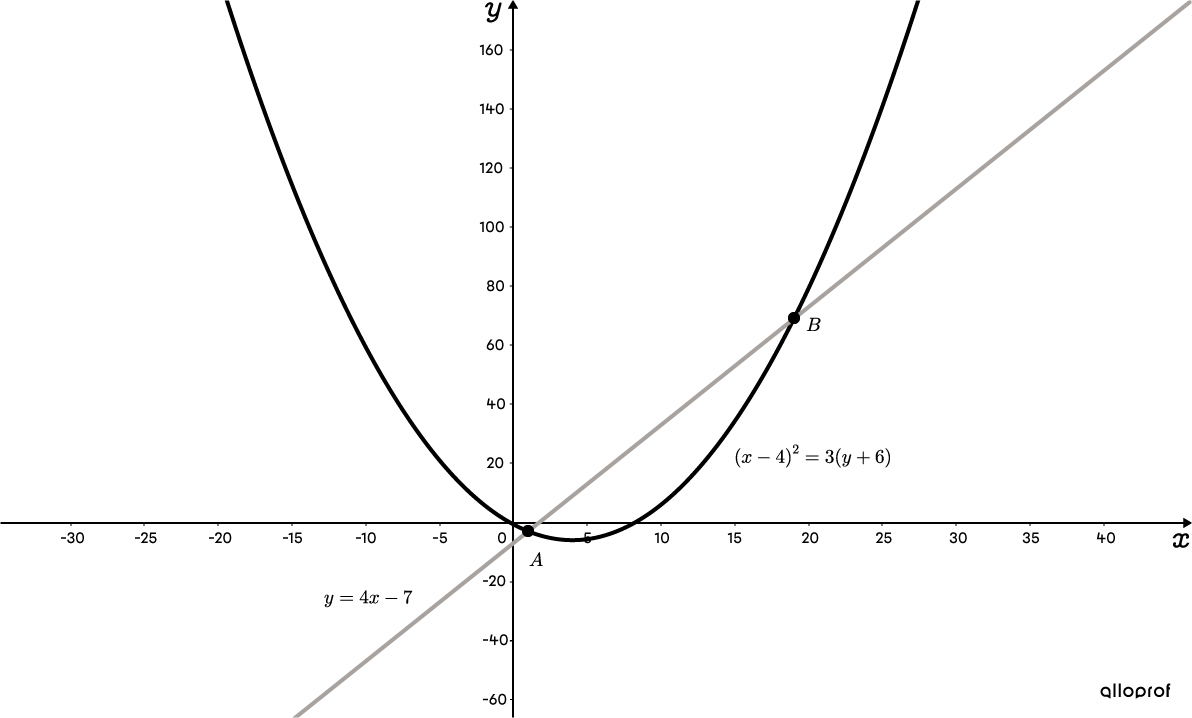
Use substitution method
We use the substitution method since variable |y| in the equation of the line is already isolated. ||\begin{align}(x-4)^2&=3(\color{#3a9a38}{y}+6)\\ (x-4)^2&=3(\color{#3a9a38}{4x-7}+6)\\ (x-4)^2&=3(4x-1)\end{align}|| -
Manipulate the equation so that it equals |0|
||\begin{align}(x-4)^2&=3(4x-1)\\ x^2-8x+16&=12x-3\\ \color{#3B87CD}{1}x^2\color{#3A9A38}{-20}x+\color{#EC0000}{19}&=0\end{align}|| -
Solve the equation
Using the quadratic formula, we obtain: ||\begin{align}x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\ &=\dfrac{-(\color{#3A9A38}{-20})\pm\sqrt{(\color{#3A9A38}{-20})^2-4(\color{#3B87CD}{1})(\color{#EC0000}{19})}}{2(\color{#3B87CD}{1})}\\\\ &=\dfrac{20\pm\sqrt{324}}{2}\\\\ x_{\small{A}}&=1\\ x_{\small{B}}&=19\end{align}|| -
Substitute the values obtained in one of the starting equations
For the point |A| with |x_{\small{A}}=1,| we have: ||\begin{align}y_{\small{A}}&=4\color{#3A9A38}{x_{\small{A}}}-7\\ &=4(\color{#3A9A38}{1})-7\\ &=-3\end{align}|| As for the point |B| with |x_{\small{B}}=19,| we have: ||\begin{align}y_{\small{B}}&=4\color{#3A9A38}{x_{\small{B}}}-7\\ &=4(\color{#3A9A38}{19})-7\\ &=69\end{align}|| -
Write the coordinates of the intersection points
The coordinates of the two points of intersection between the line |y=4x-7| and the parabola |(x-4)^2=3(y+6)| are |A(1,-3)| and |B(19,69).|