The ellipse is one of the conics. It is obtained by the intersection of a cone and a plane.
An ellipse is the geometric locus of all points whose sum of the distances to 2 fixed points, called foci, is constant.
-
An ellipse has two axes of symmetry. The longest is called the major axis, and the shortest, the minor axis.
-
An ellipse has two foci, |F_1| and |F_2.|
-
An ellipse has four vertices, |V_1,| |V_2,| |V_3,| and |V_4.|
-
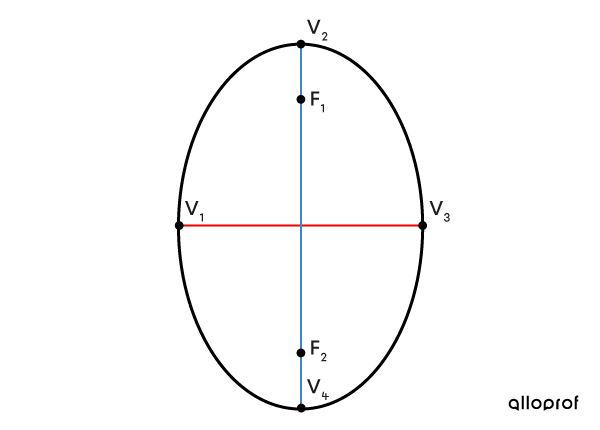
An ellipse can be vertical or horizontal.
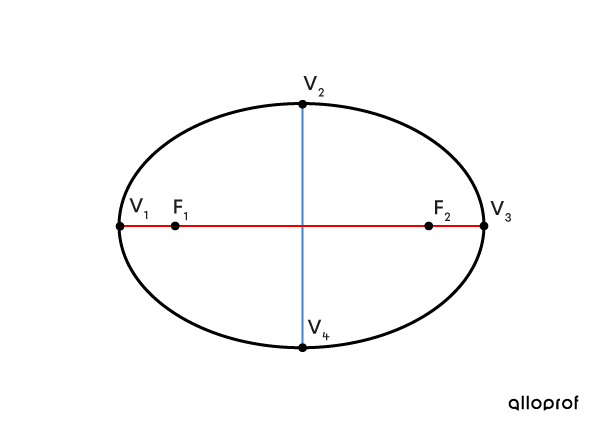
The equation that defines an ellipse centred at the origin uses parameters |a| and |b.|
||\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1|| where ||\begin{align} a &:\text{Half the length of the major axis }\\ b &: \text{Half the length of the minor axis } \end{align}||
-
If |\color{#ec0000}a < \color{#3b87cd}b,| the ellipse is vertical.
-
If |\color{#ec0000}a > \color{#3b87cd}b,| the ellipse is horizontal.
Here are the graphic representations of the two types of ellipses on which the important points are placed. The coordinates of these points in relation to the parameters of the ellipse are also given.
Vertical ellipse
The sum of the distances between a point on a vertical ellipse and its two foci is |2\color{#3b87cd}b.|
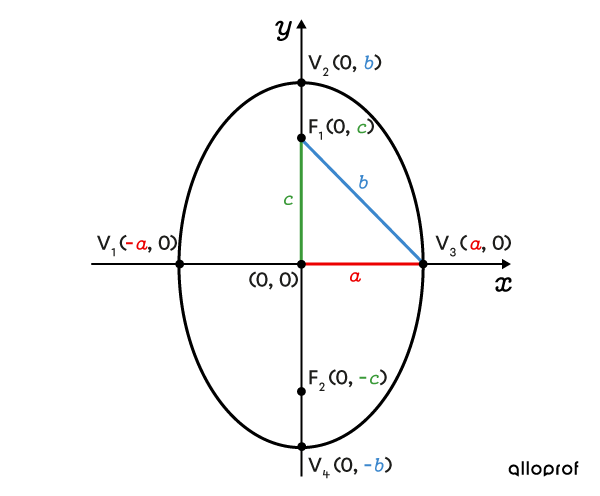
The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||
Horizontal ellipse
The sum of the distances between a point on a horizontal ellipse and its two foci is |2\color{#ec0000}a.|
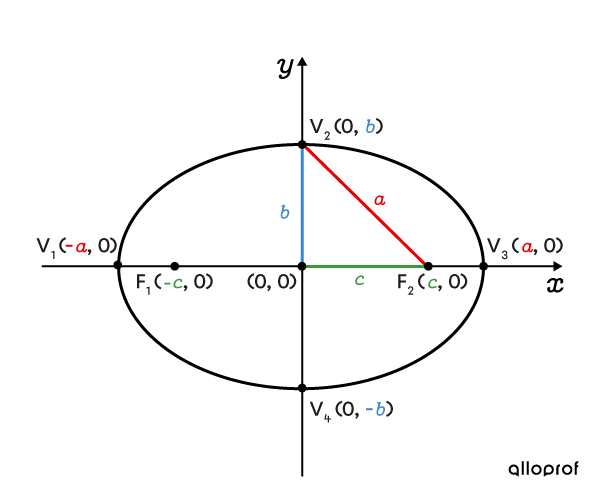
The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||
Find the value of the parameters |a| and |b| to determine the equation of an ellipse centred at the origin.
Generally, the procedure below is used.
-
Determine the value of parameter |\color{#ec0000}a,| which corresponds to half of the ellipse’s horizontal axis, and/or that of parameter |\color{#3B87CD}b,| which corresponds to half of the vertical axis.
-
If one of the two parameters is missing, find it using one of the following strategies:
a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is given, use the Pythagorean Theorem to determine the value of the missing parameter. ||\begin{align}\text{Vertical ellipse :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Horizontal ellipse :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||
b) If a point on the ellipse |(x,y)| is provided, substitute these coordinates into the equation and determine the value of the missing parameter.
-
Write the ellipse’s equation.
Determine the equation of this ellipse.
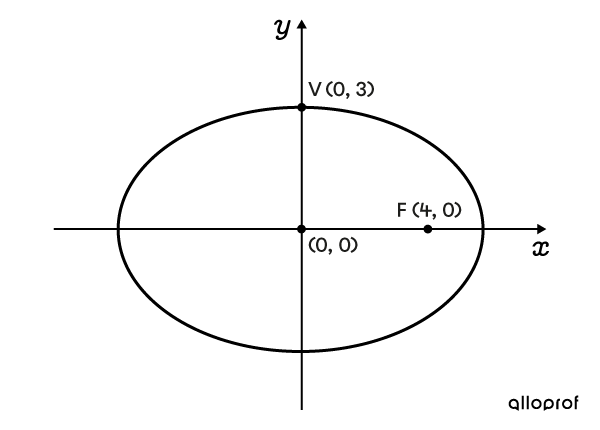
-
Determine the values of parameter |a| and/or |b|
The coordinates of one of the vertices is provided: |V(0,3),| which allows us to determine |b.| We obtain: ||\color{#3b87cd}b=\color{#3b87cd}3|| -
Find the missing parameter
The coordinates of one of the foci, |F(4,0),| is also provided. It is used to determine |c,| which is the distance between the centre and a focus. This means: ||\color{#3a9a38}c=\color{#3a9a38}4||
Since the ellipse is horizontal and parameters |b| and |c| are provided, the Pythagorean Theorem is used to find the value of |a.| This gives:
||\begin{align}\color{#3a9a38}c^2&=\color{#ec0000}a^2-\color{#3b87cd}b^2\\\color{#3a9a38}4^2&=\color{#ec0000}a^2-\color{#3b87cd}3^2\\16&=\color{#ec0000}a^2-9\\25&=\color{#ec0000}a^2\\\color{#ec0000}5&=\color{#ec0000}a\end{align}|| -
Write the equation of the ellipse
Substituting the value of parameters |a| and |b| in the basic equation results in the desired equation. ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=1\\ \dfrac{x^2}{\color{#ec0000}{5}^2}+\dfrac{y^2}{\color{#3B87CD}{3}^2}=1\\ \dfrac{x^2}{25}+\dfrac{y^2}{9}=1\end{align}||
Determine the equation of this ellipse.
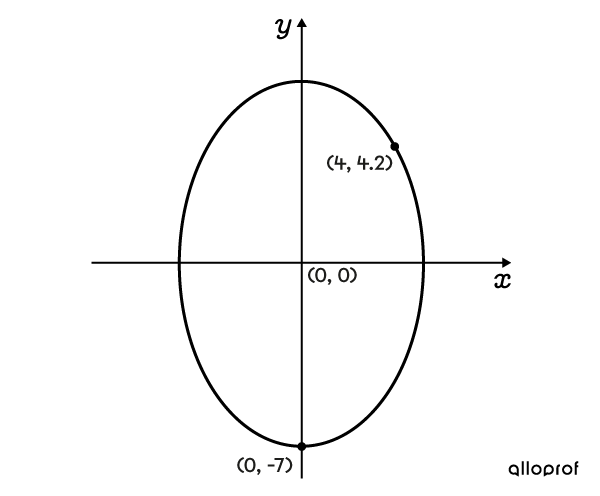
-
Determine the value of parameters |a| and/or |b|
The coordinates of one of the vertices is given: |V(0,-7)|, on the vertical axis. It is used to determine |b,| which results in:
||\color{#3b87cd}b=\color{#3b87cd}7|| -
Find the missing parameter
The coordinates of a point, |P(4,4{.}2),| are also given. In the equation, |b| is replaced with |7,| |x| with |4,| and |y| with |4{.}2,| then parameter |a| is isolated.
||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=&\ 1\\ \dfrac{4^2}{\color{#ec0000}{a}^2}+\dfrac{4{.}2^2}{\color{#3B87CD}{7}^2}=&\ 1\\ \dfrac{16}{\color{#ec0000}{a}^2}+\dfrac{17{.}64}{49}=&\ 1 \\\dfrac{16}{\color{#ec0000}{a}^2}+0{.}36=&\ 1 \\ \dfrac{16}{\color{#ec0000}{a}^2}=&\ 0{.}64 \\ 25=&\ \color{#ec0000}{a}^2\\ \color{#ec0000}{5}=&\ \color{#ec0000}a \end{align}|| -
Write the equation of the ellipse
Substituting the value of parameters |a| and |b| in the basic equation results in the desired equation. ||\begin{align}\dfrac{x^2}{\color{#ec0000}a^2}+\dfrac{y^2}{\color{#3b87cd}b^2}=1\\ \dfrac{x^2}{\color{#ec0000}{5}^2}+\dfrac{y^2}{\color{#3B87CD}{7}^2}=1\\ \dfrac{x^2}{25}+\dfrac{y^2}{49}=1\end{align}||
Follow these steps to draw an ellipse centred at the origin using its equation.
-
Mark the centre of the ellipse.
-
Use the value of parameter |\color{#EC0000}a| to mark the two vertices located on the horizontal axis. Here are the coordinates of the vertices: ||\begin{align}V_1&=(\color{#EC0000}{-a},0)\\ V_3&=(\color{#EC0000}a,0)\end{align}||
-
Use the value of parameter |\color{#3B87CD}b| to mark the two vertices located on the vertical axis. Here are the vertices’ coordinates: ||\begin{align}V_2&=(0,\color{#3B87CD}b)\\ V_4&=(0,\color{#3B87CD}{-b})\end{align}||
-
Connect the four vertices to draw the ellipse.
Draw the ellipse represented by the following equation. ||\dfrac{x^{2}}{289}+\dfrac{y^{2}}{196}=1||
-
Mark the centre of the ellipse
In an ellipse centred at the origin, the centre is point |(0,0).| -
Mark the two vertices on the horizontal axis
We have |\color{#ec0000}{a}=\sqrt{289}=\color{#ec0000}{17}.| Mark the two vertices. ||\begin{align}V_1=&\ (-17,0)\\V_3=&\ (17,0)\end{align}|| -
Mark the two vertices on the vertical axis
We have |\color{#3b87cd}b=\sqrt{196}=\color{#3b87cd}{14}.| Mark the two vertices.
||\begin{align}V_2=&\ (0,14)\\V_4=&\ (0,-14)\end{align}||
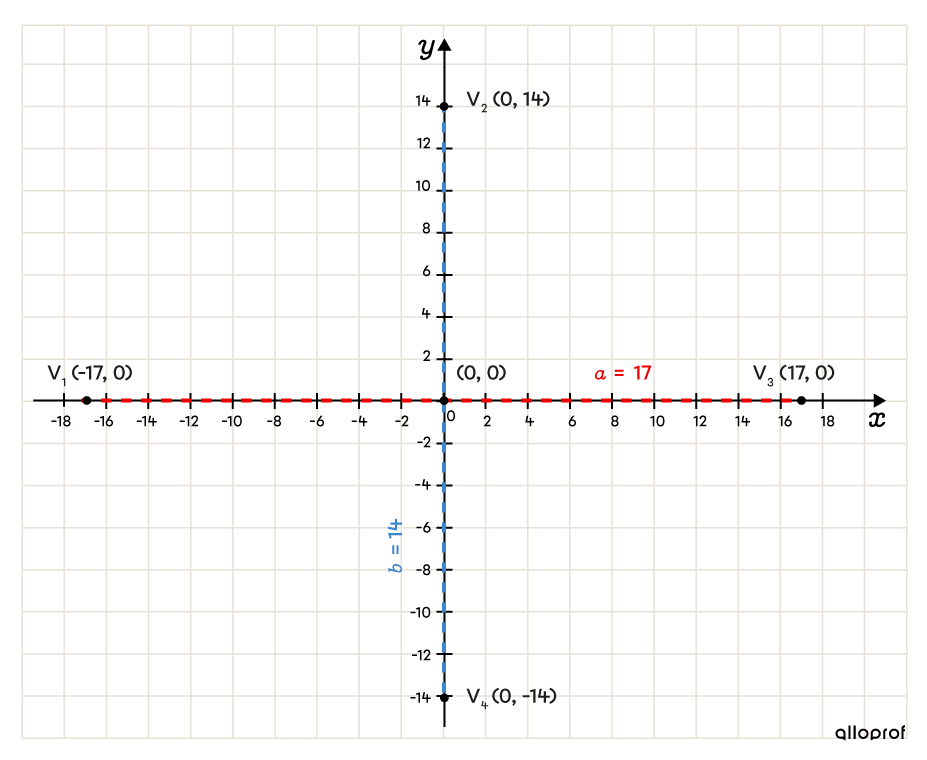
-
Sketch the ellipse
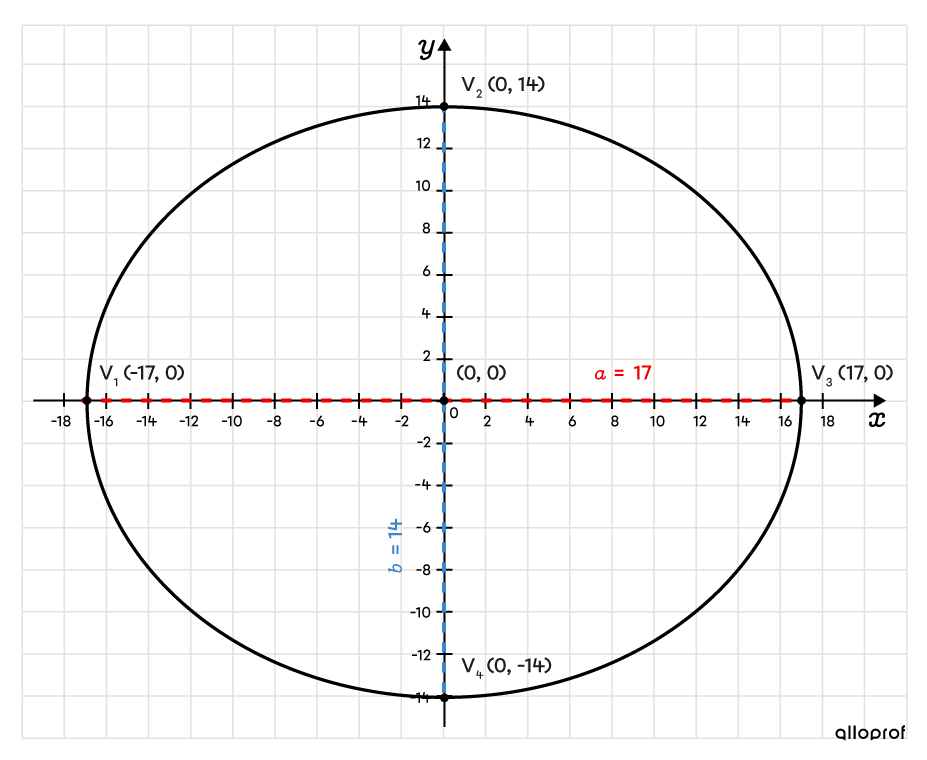
The equation that defines an uncentered ellipse uses parameters |a,| |b,| |h,| and |k.|
||\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|| or ||\begin{align} a &:\text{Half the length of the horizontal axis }\\ b &: \text{Half the length of the vertical axis }\\ (h,k) &: \text{Coordinates of the ellipse’s centre }\end{align}||
-
If |\color{#ec0000}a < \color{#3b87cd}b,| the ellipse is vertical.
-
If |\color{#ec0000}a > \color{#3b87cd}b,| the ellipse is horizontal.
Vertical ellipse
The sum of the distances between a point on a vertical ellipse and its two foci is |2\color{#3b87cd}b.|
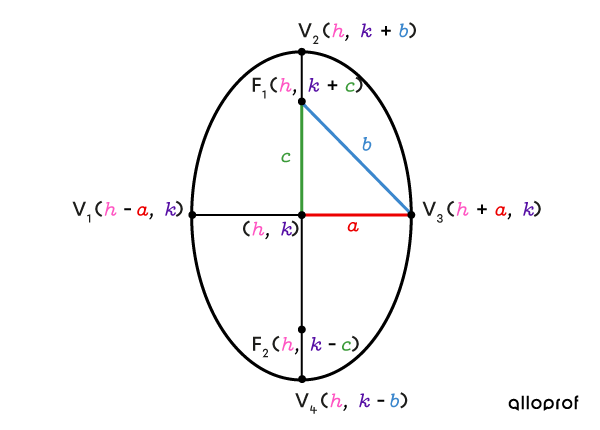
The relationship between the parameters |\color{#ec0000}a,| |\color{#3b87cd}b| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||
Horizontal ellipse
The sum of the distances between a point on a horizontal ellipse and its two foci is |2\color{#ec0000}a.|
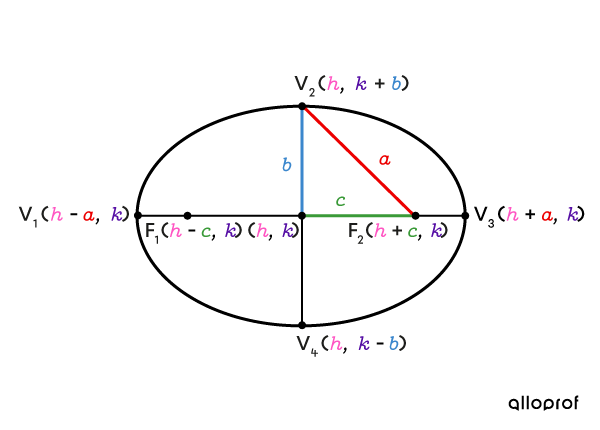
The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||
To use a graph to determine the equation of an ellipse not centred at the origin, find the value of parameters |a,| |b,| |h,| and |k.|
Generally, the process looks like this.
-
Determine the values of parameters |\color{#FF55C3}h| and |\color{#560FA5}k| from the coordinates of the ellipse’s centre.
-
Determine the value of parameter |\color{#ec0000}a,| which corresponds to half of the ellipse’s horizontal axis, and/or that of parameter |\color{#3B87CD}b,| which corresponds to half of the vertical axis.
-
If either parameter |a| or |b| is missing find it using one of the following strategies:
a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is provided, use the Pythagorean Theorem to determine the missing parameter’s value. ||\begin{align}\text{Vertical ellipse :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Horizontal ellipse :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||
b) If a point on ellipse |(x,y)| is provided, substitute its coordinates into the equation and determine the value of the missing parameter.
-
Write the ellipse’s equation.
Determine the equation of this ellipse.
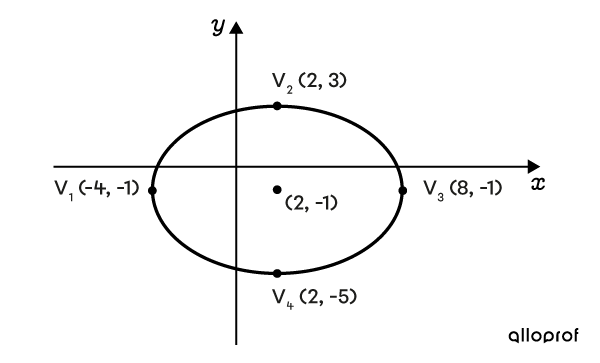
-
Determine the value of parameters |h| and |k|
The ellipse is centred at point |(2,-1),| which gives the following |h| and |k| parameters. ||\begin{align} \color{#ff55c3}{h}&=\color{#ff55c3}{2}\\ \color{#560fa5}{k}&=\color{#560fa5}{-1} \end{align}|| -
Determine the value of parameters |a| and |b|
The value of each of the ellipse’s vertices is given. So, it is possible to determine the value of |a| and |b| directly, which corresponds to the half measurement of the horizontal and vertical axes, respectively.
Since the horizontal axis measures |12| units and the vertical axis measures |8| units, the parameters of |a| and |b| are: ||\begin{align} \color{#ec0000}{a}&=\color{#ec0000}{6}\\ \color{#3b87cd}{b}&=\color{#3b87cd}{4} \end{align}|| -
Determine the value of missing parameters
For this example, all the information needed to write the equation is provided. -
Write the ellipse’s equation
Substituting the value of parameters in the basic equation results in the desired equation being found. ||\begin{align}\dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}=1\\ \dfrac{(x-\color{#ff55c3}{2})^{2}}{\color{#ec0000}{6}^2}+\dfrac{(y-(\color{#560fa5}{-1}))^{2}}{\color{#3B87CD}{4}^2}=1\\ \dfrac{(x-2)^{2}}{36}+\dfrac{(y+1)^{2}}{16}=1\end{align}||
Determine the equation of this ellipse, knowing that its horizontal axis measures |16| units.
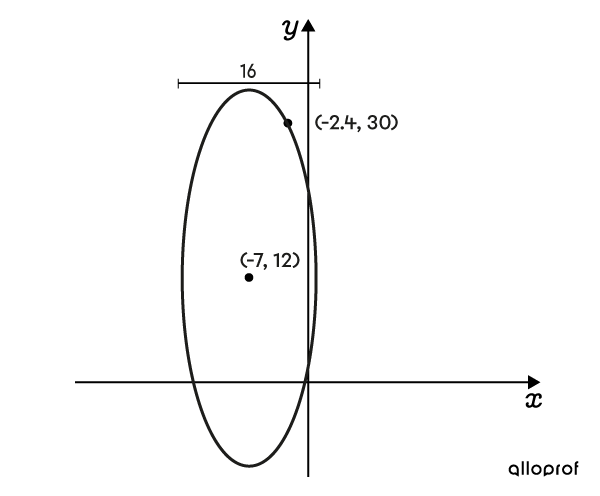
-
Determine the values of parameter |h| and |k|
The ellipse is centred at point |(-7,12),| which gives the following |h| and |k| parameters. ||\begin{align} \color{#ff55c3}{h}&=\color{#ff55c3}{-7}\\ \color{#560fa5}{k}&=\color{#560fa5}{12} \end{align}|| -
Determine the values of parameter |a| and |b|
The length of the horizontal axis is given. Therefore, the value of |a| can be determined directly.
Since the horizontal axis measures |16| units, the result is: ||\color{#ec0000}{a}=\color{#ec0000}{8}|| -
Determine the value of missing parameters
The only missing value is parameter |b.| Find it by substituting point |(-2{.}4,30)| in the equation. ||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}&=1\\ \dfrac{(-2{.}4-(\color{#ff55c3}{-7}))^{2}}{\color{#ec0000}{8}^2}+\dfrac{(30-\color{#560fa5}{12})^{2}}{\color{#3B87CD}{b}^2}&=1\\ \dfrac{21{.}16}{64}+\dfrac{324}{\color{#3B87CD}b^2}&=1\\ \dfrac{529}{1\ 600}+\dfrac{324}{\color{#3B87CD}b^2}&=1\\ \dfrac{324}{\color{#3B87CD}b^2}&=\dfrac{1\ 071}{1\ 600}\\ 1\ 071\color{#3B87CD}b^2&=518\ 400\\ \color{#3B87CD}{b}^2&\approx484{.}03\\ \color{#3b87cd}{b}&\approx\color{#3b87cd}{22} \end{align}|| -
Write the equation of the ellipse
Replacing the value of the parameters in the basic equation results in the desired equation. ||\begin{align} \dfrac{(x-\color{#ff55c3}h)^{2}}{\color{#ec0000}a^2}+\dfrac{(y-\color{#560fa5}k)^{2}}{\color{#3b87cd}b^2}&=1\\ \dfrac{(x-(\color{#ff55c3}{-7}))^{2}}{\color{#EC0000}{8}^2}+\dfrac{(y-\color{#560fa5}{12})^{2}}{\color{#3b87cd}{22}^2}&=1\\ \dfrac{(x+7)^{2}}{64}+\dfrac{(y-12)^{2}}{484}&=1\\ \end{align}||
Follow these steps to draw an ellipse using its equation.
-
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and mark the ellipse’s centre.
-
Use the value of parameter |\color{#EC0000}a| to mark the two vertices located on the horizontal axis. Here are the vertices’ coordinates. ||\begin{align}V_1:(\color{#FF55C3}h\color{#EC0000}{-a},\color{#560FA5}k)\\ V_3:(\color{#FF55C3}h\color{#EC0000}{+a},\color{#560FA5}k)\end{align}||
-
Use the value of parameter |\color{#3B87CD}b| to place the two vertices on the vertical axis. Here are the vertices’ coordinates. ||\begin{align}V_2:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{+b})\\ V_4:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{-b})\end{align}||
-
Connect the four vertices to draw the ellipse.
Draw the ellipse represented by the following equation. ||\dfrac{(x-5)^{2}}{64}+\frac{(y+4)^{2}}{100}=1||
-
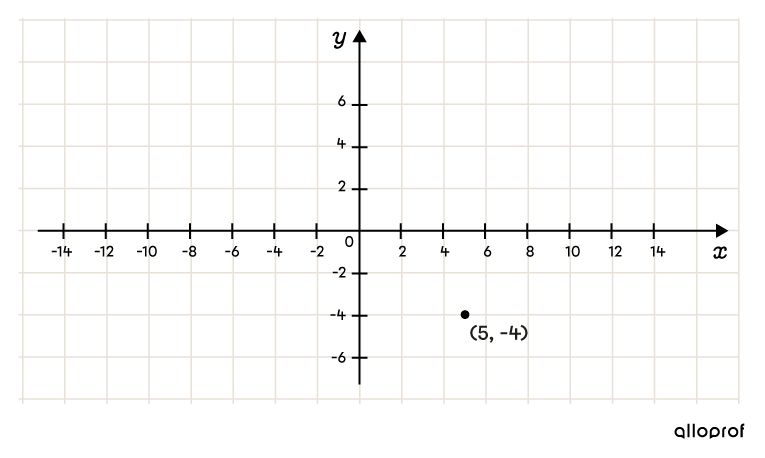
Identify parameters |h| and |k| in the equation and place the centre
According to the equation, the centre is at the following coordinates: ||(\color{#FF55C3}h,\color{#560fa5}k)=(\color{#FF55C3}5,\color{#560fa5}{-4})||
-
Mark the two vertices on the horizontal axis
The following is given: |\color{#ec0000}{a}=\sqrt{64}=\color{#ec0000}{8}.| Place the two vertices. ||\begin{align}V_1=&\ (\color{#FF55C3}5\color{#EC0000}{-8},\color{#560FA5}{-4})= (-3,-4)\\ V_3=&\ (\color{#FF55C3}5\color{#EC0000}{+8},\color{#560FA5}{-4})=(13,-4)\end{align}|| -
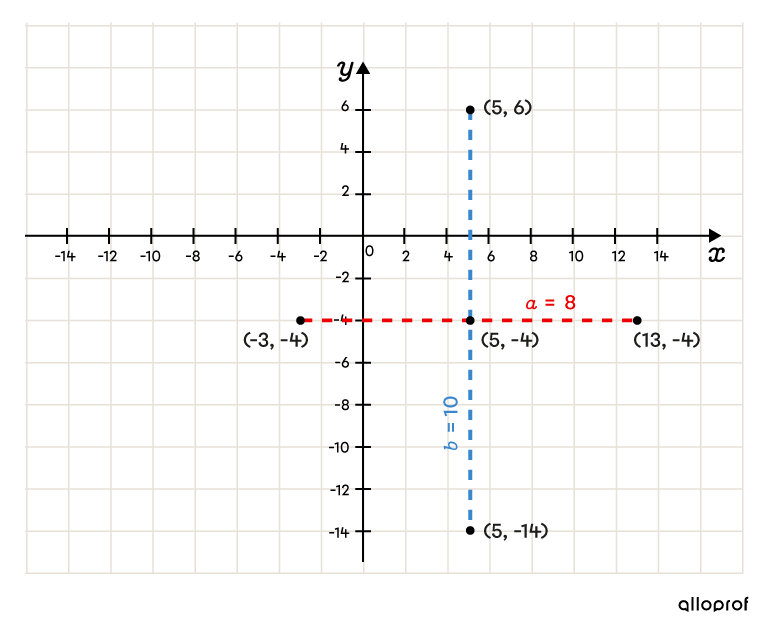
Mark the two vertices on the vertical axis
The following is given: |\color{#3B87CD}{b}=\sqrt{100}=\color{#3B87CD}{10}.| Place the two vertices. ||\begin{align}V_2=&\ (\color{#FF55C3}5,\color{#560FA5}{-4}\color{#3B87CD}{+10})= (5,6)\\ V_4=&\ (\color{#FF55C3}5,\color{#560FA5}{-4}\color{#3B87CD}{-10})=(5,-14)\end{align}||
-
Draw the ellipse
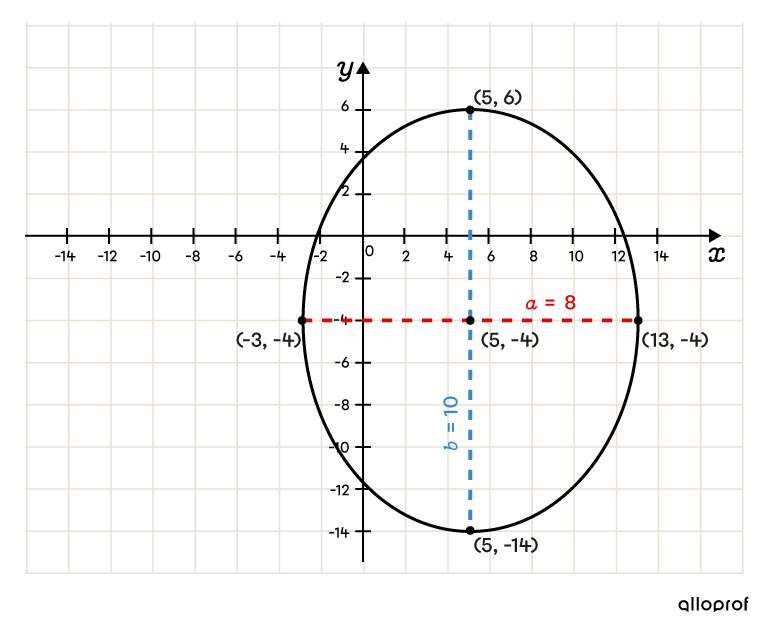
Apply the following relations to represent a region bounded by an ellipse
|
Sector of the Cartesian Plane |
Graphical Representation |
Corresponding Inequality |
|---|---|---|
|
The exterior, excluding the curve |
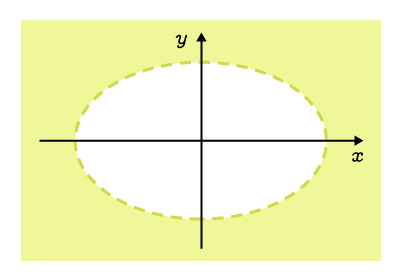 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}>1\\\\ |
|
The interior, excluding the curve |
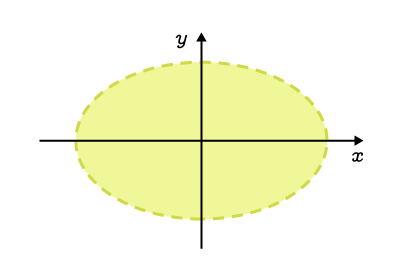 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}<1\\\\ |
|
The exterior, including the curve |
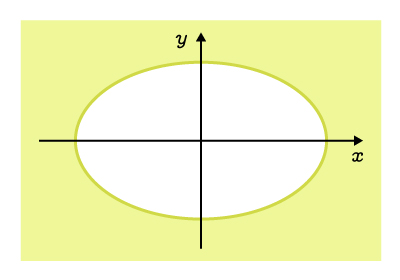 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\geq1\\\\ |
|
The interior, including the curve |
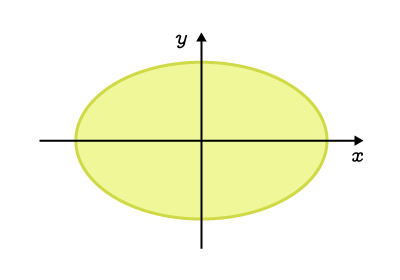 |
||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\leq1\\\\ |
The general form of the equation of all conics, including the ellipse, for which the horizontal axis is parallel to the x-axis and the vertical axis is parallel to the y-axis is: || Ax^2+ By^2+Cx+Dy+E=0||
It can be helpful to switch from general form to standard form when solving some problems concerning the ellipse.
Determine the ellipse’s focal length (distance between the two foci) represented by the following equation. ||x^2+9y^2 + 8x - 18y - 56 = 0||
-
Factor the equation by completing the square
Combine terms that share the same variable. ||\color{#3a9a38}{x^2+8x}+\color{#3B87CD}{9y^2-18y}-56=0||
Complete the square twice; once for the terms with variable x and again for the terms with variable y.
For terms with variable |x,| we get the following equation. ||\begin{align} \color{#3a9a38}{x^2+8x}&=(x)^2+2(x)(4)\color{#fa7921}{+(4)^2-(4)^2}\\ \color{#3a9a38}{x^2+8x}&=\color{#3a9a38}{(x+4)^2-16} \end{align}|| As for the terms with variable |y,| we get the following equation: ||\begin{align}\color{#3B87CD}{9y^2-18y}&=9\Big(y^2-2y\Big)\\ \color{#3B87CD}{9y^2-18y}&=9\Big((y)^2-2(y)(1)\color{#fa7921}{+(1)^2-(1)^2}\Big)\\ \color{#3B87CD}{9y^2-18y}&=9\Big((y-1)^2-1\Big)\\ \color{#3B87CD}{9y^2-18y}&=\color{#3B87CD}{9(y-1)^2-9}\\ \end{align}||
Substitute the expressions found when completing the square for the terms with variables |x| and |y| into the original equation and then simplify the constant terms. ||\begin{align} \color{#3a9a38}{x^2+8x}+\color{#3B87CD}{9y^2-18y}-56&=0\\ \color{#3a9a38}{(x+4)^2-16}+\color{#3B87CD}{9(y-1)^2-9}-56&=0\\ (x+4)^2+9(y-1)^2-81&=0\\ \end{align}|| -
Manipulate this equation to find the equation in standard form
Since the standard form of an ellipse is equal to |1| , we have to do some manipulations. ||\begin{align} (x+4)^2+9(y-1)^2-81&=0\\ (x+4)^2+9(y-1)^2&=81\\ \dfrac{(x+4)^2}{81}+\dfrac{9(y-1)^2}{81}&=\dfrac{81}{81} \\ \dfrac{(x+4)^2}{81}+\frac{(y-1)^2}{9}&=1\\ \end{align}|| -
Find the values of |a| and |b|
The values of |a| and |b| must be found when searching for the focal length. To achieve this, find the square roots of the two denominators. ||\begin{align} \dfrac{(x+4)^2}{81} + \dfrac{(y-1)^2}{9} &=1\\ \dfrac{(x+4)^2}{\color{#ec0000}9^2} + \dfrac{(y-1)^2}{\color{#3b87cd}3^2} &=1\end{align}|| -
Calculate the value of |c|
Since |a > b,| the following equation is used: ||\begin{align}\color{#3a9a38}c^2&=\color{#ec0000}a^2-\color{#3b87cd}b^2\\ \color{#3a9a38}c^2&= \color{#ec0000}9^2-\color{#3b87cd}3^2\\ \color{#3a9a38}c^2&=81-9\\ \color{#3a9a38}c^2&=72\\ \color{#3a9a38}c\ &\approx \color{#3a9a38}{8{.}5}\end{align}||
Therefore, the focal length of this ellipse is |2 \times 8{.}5 = 17.|