Circles are part of the conics. It is obtained by the intersection of a cone and a plane.
The circle is the geometric locus of all points equidistant from a point called the centre.
Any point |(x,y)| that belongs to a circle can be found using Pythagorean Theorem (also called the Pythagorean Relation).
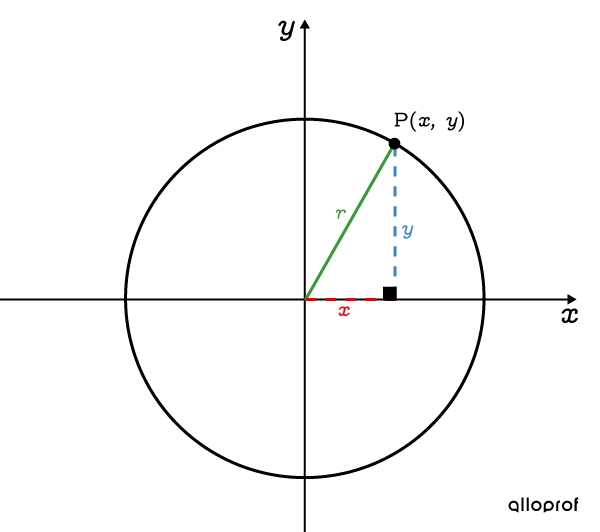
The equation that defines a circle centred at the origin uses parameter |r.|
||x^2+ y^2= r^2||
where
||r=\text{radius of a circle}||
The value of radius |r| must be found to determine the equation of a circle centred at the origin.
-
Find the value of parameter |\color{#3a9a38}r,| the circle’s radius. If necessary, substitute |x| and |y| with a point on the circle and solve the equation.
-
Write the equation of the circle.
Find the equation of the circle centred at the origin that passes through point |(7,-3).|
-
Find the value of parameter |r|
Replace |x| and |y| in the equation for a circle centred at the origin. ||\begin{align}x^2+ y^2&= \color{#3a9a38}r^2\\7^2+ (-3)^2&=\color{#3a9a38}r^2\\49+9&=\color{#3a9a38}r^2\\ 58&=\color{#3a9a38}r^2\\ \sqrt{58}&=\color{#3a9a38}r\end{align}|| -
Write the equation of the circle
The desired equation is found by substituting the value of parameter |r| with |\sqrt{58}| in the basic equation: ||\begin{align}x^2+y^2&=\color{#3a9a38}r^2\\ x^2+y^2&=(\color{#3a9a38}{\sqrt{58}})^2\\ x^2+y^2&=58\end{align}||
-
Place the centre of the circle at the origin of the Cartesian plane.
-
Use the equation to find parameter |\color{#3a9a38}r|.
-
Starting from the centre, use a compass to sketch a circle whose radius is equal to |\color{#3a9a38}r.|
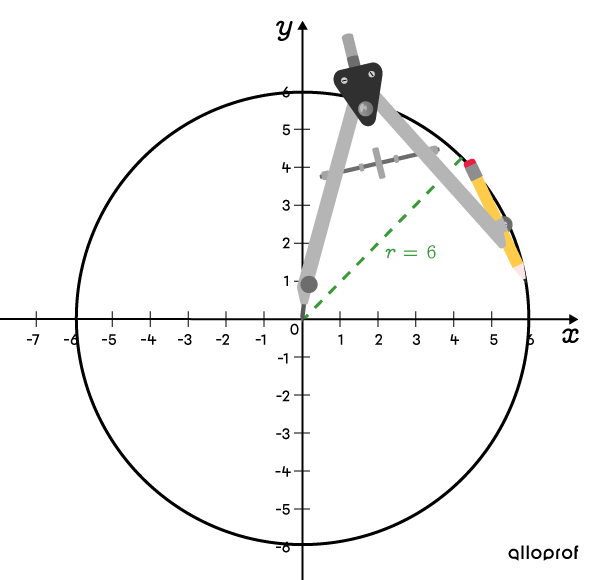
Sketch the circle of the equation |x^2+y^2=36.|
-
Place the centre of the circle
Since the circle is centred at the origin, the centre is |(0,0).| -
Find parameter |r|
||\color{#3a9a38}r=\sqrt{36}=\color{#3a9a38}6|| -
Use a compass to sketch the circle
The Pythagorean Theorem can be used for any point |(x,y)| that belongs to the circle even if it is not centred at the origin.
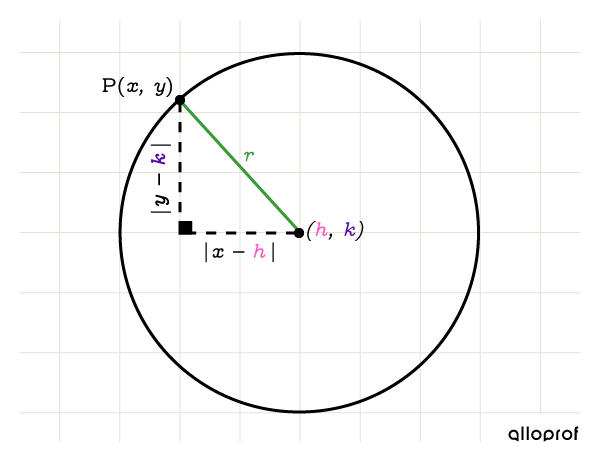
The equation that defines a circle not centred at the origin uses parameters |r,| |h,| and |k.|
||(x-h)^2+(y-k)^2= r^2||
where
||\begin{align} r&=\text{radius of the circle}\\ (h,k)&=\text{coordinates of the circle’s centre}\end{align}||
Find the value of radius |r| and coordinates |(h, k)| of the centre to find the equation of a circle not centred at the origin.
-
Find the values of parameters |\color{#FF55C3}h| and |\color{#560FA5}k| from the coordinates of the circle’s centre.
-
Find the value of parameter |\color{#3a9a38}r,| the radius of the circle. If necessary, substitute |x| and |y| with a point on the circle. Then, solve the equation.
-
Write the equation of the circle.
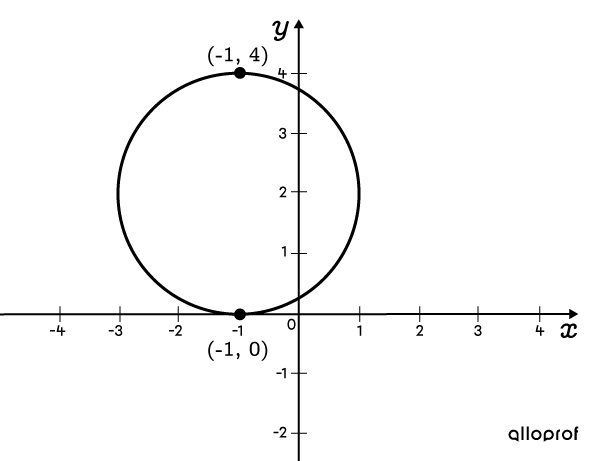
Find the equation of a circle which passes through points |(-1, 0)| and |(-1, 4).|
-
Find the values of parameters |h| and |k|
Note that the two points given are opposite each other since they have the same x-value but not the same y-value. Thus, the segment that connects them is the diametre and the midpoint of this segment is the circle’s centre. The centre has the same x-value as the two points: |\color{#ff55c3}h=\color{#ff55c3}{-1}.| All that remains is finding the y-value of the circle’s centre. ||\color{#560fa5}k=\dfrac{4+0}{2} =\color{#560fa5}{2}|| -
Find the value of parameter |r|
Since the circle’s diameter measures |4,| its radius is ||\color{#3a9a38}r=\dfrac{4}{2}=\color{#3a9a38}2|| -
Write the equation of the circle
It equals: ||\begin{align}(x-\color{#ff55c3}h)^2+(y-\color{#560fa5}k)^2&= \color{#3a9a38}r^2\\ \big(x-(\color{#ff55c3}{-1})\big)^2+(y-\color{#560fa5}2)^2&=\color{#3a9a38}{2}^2\\ (x+1)^2+(y-2)^2&=4\end{align}||
-
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and place the centre of the circle.
-
Determine parameter |\color{#3a9a38}r| in the equation.
-
Starting from the centre, use a compass to sketch a circle whose radius is equal to |\color{#3a9a38}r.|
Sketch the circle with the equation: |(x+4)^2+(y-3)^2=16.|
-
Identify parameters |h| and |k| in the equation and place the centre of the circle
According to the equation, the centre is located at the following coordinates: ||(\color{#FF55C3}h,\color{#560FA5}k)=(\color{#FF55C3}{-4},\color{#560FA5}{3})||
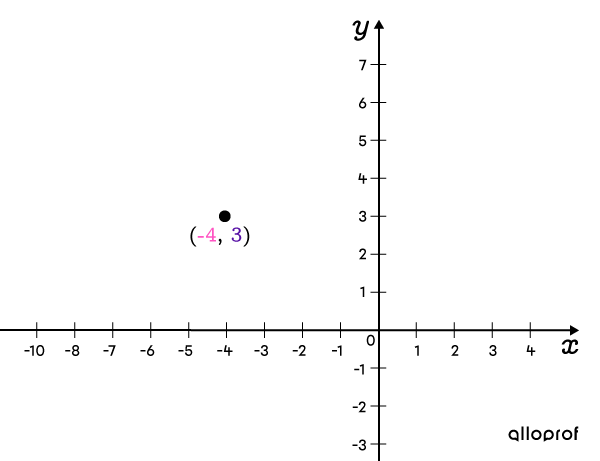
-
Determine parameter |r|
||\color{#3a9a38}r=\sqrt{16}=\color{#3a9a38}4|| -
Use a compass to sketch the circle
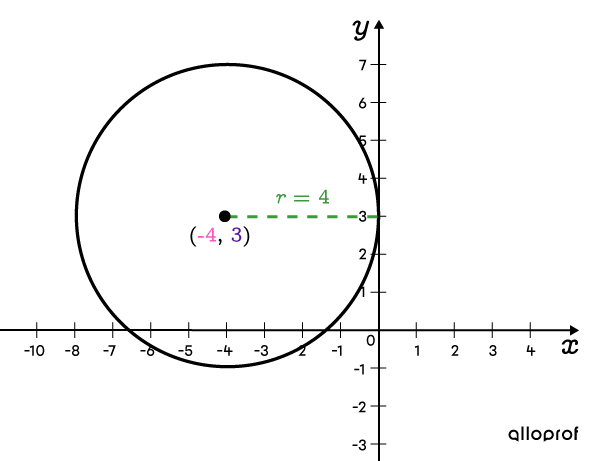
When we want to represent a region bounded by a circle, we apply the following relations.
|
Sector of the Cartesian Plane |
Graphic Representation |
Corresponding Inequality |
|---|---|---|
|
The exterior, excluding the curve |
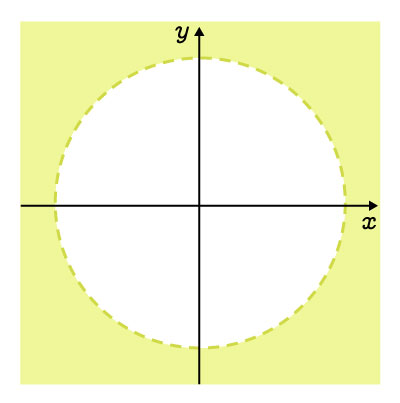 |
||\begin{align}x^2&+y^2>r^2\\\\(x-h)^2&+(y-k)^2>r^2\end{align}|| |
|
The interior, excluding the curve |
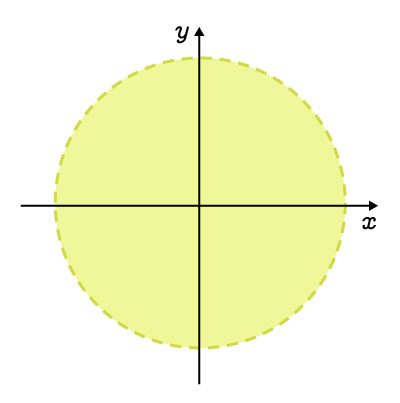 |
||\begin{align}x^2&+y^2<r^2\\\\(x-h)^2&+(y-k)^2<r^2\end{align}|| |
|
The exterior, including the curve |
 |
||\begin{align}x^2&+y^2\geq r^2\\\\(x-h)^2&+(y-k)^2\geq r^2\end{align}|| |
|
The interior, including the curve |
 |
||\begin{align}x^2&+y^2\leq r^2\\\\(x-h)^2&+(y-k)^2\leq r^2\end{align}|| |
A tangent to a circle is a line perpendicular to the radius that passes through the point of tangency.
-
Find the slope of the line that passes through the centre of the circle and the point of tangency.
-
Find the slope of the tangent line using the relationship between two perpendicular lines.
-
Find the y-intercept of the tangent line using its slope and the coordinates of the point of tangency.
-
Write the tangent line’s equation.
Find the equation of the line tangent to the circle with the following equation: |(x+1)^2+(y-2)^2=25| at the point |(2,6).|
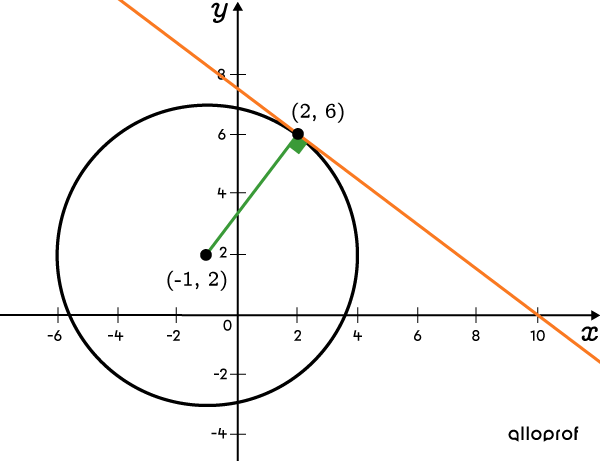
-
Find the slope of the line that passes through the centre of the circle and the given point
The circle’s centre is located at coordinates |(-1,2).| Calculate the slope of the line that passes through the circle’s centre and the point of tangency |(2,6).| ||\begin{align}a&=\frac{y_2-y_1}{x_2-x_1}\\ \\&= \frac{6-2}{2--1}\\ \\&=\frac{4}{3}\end{align}|| -
Find the slope of the tangent line
The slope of the tangent line is always the negative reciprocal of the slope of the line that passes through the circle’s centre and the point of tangency. So, the slope of the tangent line is |a = - \dfrac{3}{4}.| -
Find the y-intercept of the tangent line
Substitute |a| with the slope of the tangent line and |x| and |y| with the coordinates of the point of tangency to find the y-intercept. This gives: ||\begin{align}y&=ax+b \\ 6&={-\dfrac{3}{4}}(2)+b\\6&=-\dfrac{3}{2}+b\\ \dfrac{15}{2}&=b\end{align}|| -
Write the equation of the tangent line
So, the tangent line’s equation is: ||y =-\dfrac{3}{4}x +\dfrac{15}{2}||
The general form of the equation of all conics, including the circle, for which the horizontal axis is parallel to the x-axis and the vertical axis is parallel to the y-axis is: || Ax^2+ By^2+Cx+Dy+E=0.||
Expand the standard form of the equation of a circle to find the general form: ||\begin{align}(x-h)^2 + (y-k)^2 &= r^2\\ (x-h)(x-h) + (y-k)(y-k) &= r^2 \\ x^2 - 2hx + h^2 + y^2 - 2ky + k^2 &= r^2 \\x^2 + y^2 - 2hx - 2ky + h^2 + k^2 &= r^2 \\ x^2 + y^2 \color{#ec0000}{- 2h}x \color{#3b87cd}{- 2k}y +\color{#3a9a38}{(h^2 + k^2 - r^2)} &=0 \\ x^2 + y^2 + \color{#ec0000}{C}x + \color{#3b87cd}{D}y + \color{#3a9a38}{E} &= 0\end{align}||
where ||\begin{align}A&=1\\B&=\ 1\\\color{#ec0000}{C}&=\color{#ec0000}{-2h}\\ \color{#3b87cd}D&=\color{#3b87cd}{-2k}\\ \color{#3a9a38}E&=\color{#3a9a38}{h^2 + k^2 - r^2}\end{align}||