Sometimes we are looking for missing measurements in plane figures. To find them, you must solve a system of equations using the comparison method, substitution method or elimination method. You also need to know the perimeter and area formulas. Here are the steps to follow to do so.
-
Create a system of 2 equations using the information given in the problem.
-
Solve the system of equations.
-
Answer the question.
Here are a series of examples. The first are geometry problems that do not have a specific context, while the last 2 are word problems that present a short situation.
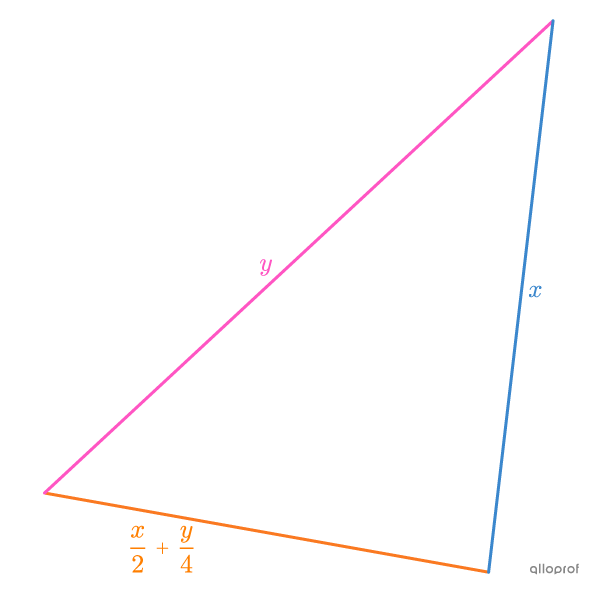
In the following triangle, |y| represents the longest side, |\dfrac{x}{2}+\dfrac{y}{4}| represents the shortest side and |x| represents the 3rd side.
Find the measure of each of the sides if the perimeter of the triangle is |49\ \text{cm}| and the length of the shortest side is |13\ \text{cm}.|
-
Create a system of 2 equations
1st equation
The 1st equation is created using the perimeter.
||\begin{align}P&=\,\text{Sum of all sides}\\49&=x+y+\dfrac{x}{2}+\dfrac{y}{4}\end{align}||
We eliminate the fractions by multiplying both sides of the equation by |4,| and reducing.
||\begin{align}49\color{#ec0000}{\times4}&=\color{#ec0000}{\left(\color{black}{x+y+\dfrac{x}{2}+\dfrac{y}{4}}\right)\times4}\\196&=4x+4y+2x+y\\196&=6x+5y\end{align}||
2nd equation
The 2nd equation is created using the information about the shortest side.
||\begin{align}13&=\text{Measure of the shortest side}\\
13&=\dfrac{x}{2}+\dfrac{y}{4}
\end{align}||
We eliminate the fractions by multiplying both sides of the equation by |4.|
||\begin{align}
13\color{#ec0000}{\times4}&=\color{#ec0000}{\left(\color{black}{\dfrac{x}{2}+\dfrac{y}{4}}\right)\times4}\\
52&=2x+y\end{align}||
-
Solve the system of equations
It’s possible to use the elimination method to solve this system of equations. We begin by multiplying the 2nd equation by |3| to make the coefficient of |x| the same in both equations.
||\begin{align}\color{#ec0000}{3\times \big(}52&=2x+y\color{#ec0000}{\big)}\\156&=6x+3y\end{align}||
We subtract the 2nd equation from the 1st.
||\begin{align}196&=6x+5y\\ -\ (156&=6x+3y)\\\hline40&=0x+2y\end{align}||
We solve the newly obtained equation.
||\begin{align}40&=2y\\20&=y\end{align}||
We find the |x| value by substituting |y| with |20| in one of the 2 equations.
||\begin{align}52&=2x+\color{#3a9a38}y\\ 52&=2x+\color{#3a9a38}{20}\\ 32&=2x\\ 16&= x\end{align}||
-
Answer the question
Therefore, the longest side measures |20\ \text{cm}.|
To find the measure of the small side, we replace |x| with |16| and |y| with |20| in the algebraic expression.
||\begin{align}\text{Small side}&=\dfrac{\color{#3a9a38}x}{2}+\dfrac{\color{#3a9a38}y}{4}\\&=\dfrac{\color{#3a9a38}{16}}{2}+\dfrac{\color{#3a9a38}{20}}{4}\\&=8+5\\&=13\ \text{cm}\end{align}||
The 3rd side measures |16\ \text{cm.}|
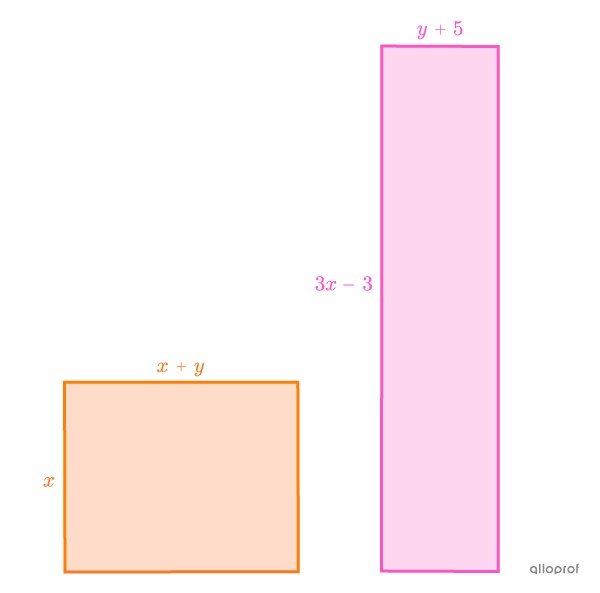
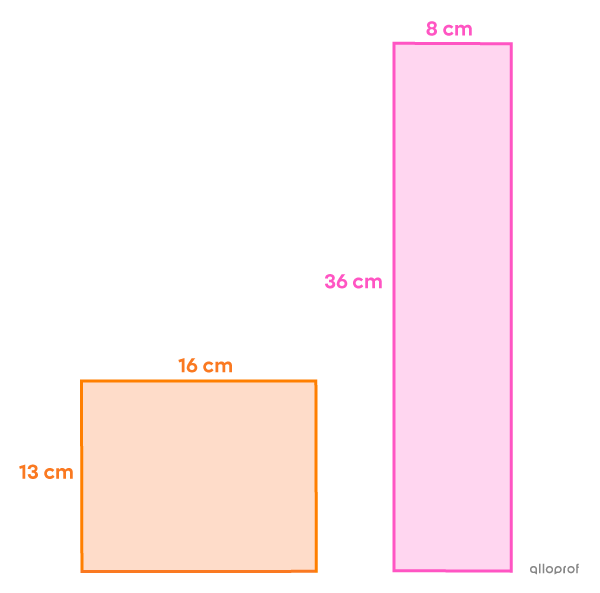
What is the measure of each of the sides of the 2 following rectangles if their respective perimeters are |58\ \text{cm}| and |88\ \text{cm}|?
-
Create a system of equations
1st equation
The 1st equation is created using the perimeter of the 1st rectangle.
||\begin{align}P&=\text{Sum of all sides}\\
58 &= x + x + (x+y) + (x+y) \\
58 &= 4x +2y\end{align}||
2nd equation
The 2nd equation is created using the perimeter of the 2nd rectangle.
||\begin{align}P&= \text{Sum of all sides}\\ 88 &= (3x-3)+(3x-3)+(y+5)+(y+5)\\
88 &= 6x + 2y +4 \\
84&= 6x+2y\end{align}||
-
Solve the system of equations
We can use the comparison method to solve this system of equations. To do so, we must isolate |y| in both equations.
||\begin{align}58 &= 4x +2y\\58-4x&=2y\\29-2x&=y\end{align}||
||\begin{align}84&= 6x+2y\\84-6x&=2y\\42-3x&=y\end{align}||
We can now apply the comparison method and solve the equation.
||\begin{align}y&=y\\29-2x&=42-3x\\x&=13\end{align}||
Substituting |x| with |13| in one of the 2 starting equations, we find the |y| value.
||\begin{align}58&=4\color{#3a9a38}x+2y\\ 58&=4\color{#3a9a38}{(13)}+2y\\58&=52+2y\\ 6&=2y&\\ 3&=y\end{align}||
-
Answer the question
Therefore, here are the measures of each side of the 2 rectangles.
Width of the 1st rectangle: |x=13\ \text{cm}|
Length of the 1st rectangle: |x+y=13+3=16\ \text{cm}|
Width of the 2nd rectangle: |3x-3=3(13)-3=36\ \text{cm}|
Length of the 2nd rectangle: |y+5=3+5=8\ \text{cm}|
How long are the diagonals of the following 2 rhombuses if they have respective areas of |17.28\ \text{cm}^2| and |17.2\ \text{cm}^2|?

-
Create a system of equations
1st equation
The 1st equation is created using the 1st rhombus.||\begin{align}A &=\dfrac{D \times d}{2}\\ 17.28&=\dfrac{6 (y-x)}{2}\\ 17.28&=3y-3x\end{align}||
2nd equation
The 2nd equation is created using the 2nd rhombus.||\begin{align}A&=\dfrac{D \times d}{2}\\ 17.2&=\dfrac{(x+y)\times 4}{2}\\ 17.2&= 2x + 2y\end{align}||
-
Solve the system of equations
We can use the comparison method to solve this system of equations. To do so, we must isolate |y| in both equations.
||\begin{align}17.28&=3y-3x\\17.28+3x&=3y\\5.76+x&=y\end{align}||
||\begin{align}17.2&= 2x + 2y\\17.2-2x&=2y\\8.6-x&=y\end{align}||
We can now apply the comparison method and solve the equation.
||\begin{align}\color{#3b87cd}{y}&=\color{#ff55c3}{y}\\ \color{#3b87cd}{5.76+x}&=\color{#ff55c3}{8.6 - x}\\ 2x &= 2.84\\ x &= 1.42\end{align}||
Substituting |x| with |1.42| in one of the 2 starting equations, we find the |y| value.
||\begin{align}17.28&=\dfrac{6 (y-\color{#3a9a38}x)}{2}\\17.28 &=3(y-\color{#3a9a38}{1.42}) \\17.28 &=3y-4.26\\21.54 &= 3y \\7.18 &= y\end{align}||
-
Answer the question
Therefore, here are the measures of each diagonal of the rhombuses.
Small diagonal of the 1st rhombus: |y-x=7.18-1.42=5.76\ \text{cm}|
Large diagonal of the 1st rhombus: |6\ \text{cm}|
Small diagonal of the 2nd rhombus: |4\ \text{cm}|
Large diagonal of the 2nd rhombus: |x+y=1.42+7.18=8.6\ \text{cm}|

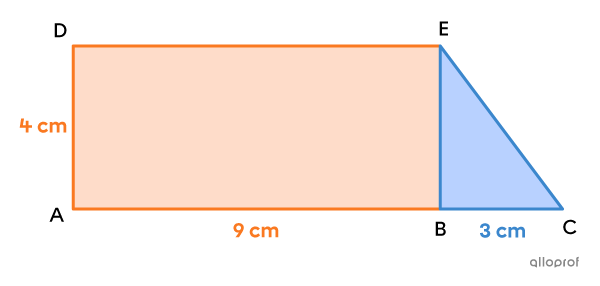
What is the measure of the sides |\overline{AD},| |\overline{AB}| and |\overline{BC}| of the trapezoid if the total area of the trapezoid is |42\ \text{cm}^2| and the area of the triangular region is |6\ \text{cm}^2|?

-
Create a system of 2 equations
1st equation
The 1st equation is created using the area of the trapezoid.
||\begin{align}A&=\dfrac{(B+b) \times h}{2}\\ 42&=\dfrac{\big((x+y)+x\big) \times \dfrac{4x}{9}}{2}\\ 42&=\dfrac{(2x+y) \times \dfrac{4x}{9}}{2}\\ 42&=\dfrac{8x^2+4xy}{18}\\ 756 &= 8x^2 +4xy\end{align}||
2nd equation
The 2nd equation is created using the area of the triangle.
||\begin{align}A&=\dfrac{b \times h}{2}\\6&=\dfrac{y \times \dfrac{4x}{9}}{2}\\ 6&= \dfrac{4xy}{18}\\108&=4xy\end{align}||
-
Solve the system of equations
Using the substitution method, we get the following equation and solve it.
||\begin{align}756&=8x^2+\color{#3a9a38}{4xy}\\ 756&=8x^2+ \color{#3a9a38}{108}\\ 648&=8x^2\\ \color{#ec0000}{\sqrt{\color{black}{81}}}&=\color{#ec0000}{\sqrt{\color{black}{x^2}}}\\ \pm\ 9&=x\end{align}||
Due to the context, we only keep the positive |x| value, since a segment cannot have a negative length. So, we substitute |x| with |9| in one of the initial equations to find the |y| value.
||\begin{align}108&=4xy\\108&=4 \times 9 \times y\\108&=36y\\3&=y\end{align}||
-
Answer the question
Here are the lengths of the segments.
Length of |\overline{AB}:| |x=9\ \text{cm}|
Length of |\overline{BC}:| |y=3\ \text{cm}|
Length of |\overline{AD}:| |\dfrac{4x}{9}=\dfrac{4(9)}{9}=4\ \text{cm}|
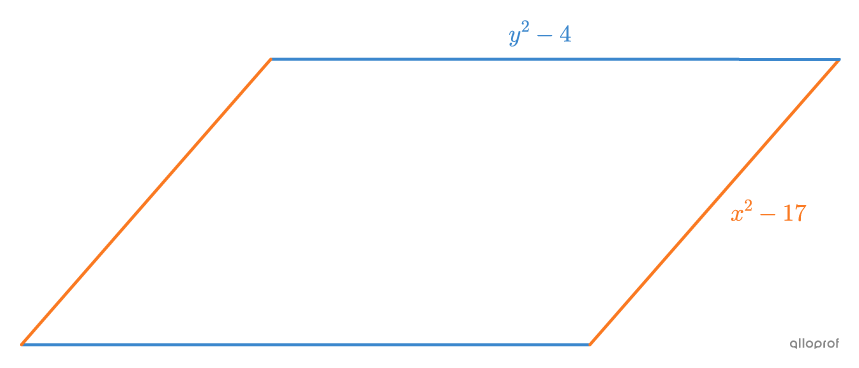
What is the measure of each side of the following parallelogram, if its perimeter is |40\ \text{cm}| and the measure of the shorter side is |\dfrac{2}{3}| the length of the longer side?
-
Create a system of 2 equations
1st equation
The 1st equation is created using the perimeter.
||\begin{align}P&= \text{Sum of all sides} \\
40 &=2\left(y^2-4\right) + 2 \left(x^2-17\right)\\
40&=2y^2-8+2x^2-34 \\
82 &= 2x^2+2y^2\end{align}||
2nd equation
The 2nd equation is created using the fact that the shortest side corresponds to |\dfrac{2}{3}| the length of the longest side.
||\begin{align}x^2-17&=\dfrac{2}{3} (y^2-4)\\ 3(x^2-17)&=2(y^2-4)\\ 3x^2-51&=2y^2-8\\-43&=-3x^2+2y^2\end{align}||
-
Solve the system of equations
Since the coefficients of |y^2| are the same in the 2 equations, we can use the elimination method.
||\begin{align}82&=\ \ \ 2x^2+2y^2\\-\ (-43&=-3x^2+2y^2)\\ \hline 125&=\ \ \ 5x^2+0y^2\end{align}||
We now solve this new equation.
||\begin{align}125&=5x^2\\25&=x^2\\\pm 5&=x\end{align}||
To find the |y| value, we can use one of the starting equations. If we use |5| or |-5,| the measure of the segment will be the same.
||\begin{align}y^2 &= 41-\color{#3a9a38}x^2\\
y^2&=41 - (\color{#3a9a38}{\pm\, 5})^2\\y^2&=41-25\\y^2&=16\\
y&=\pm 4\end{align}||
-
Answer the question
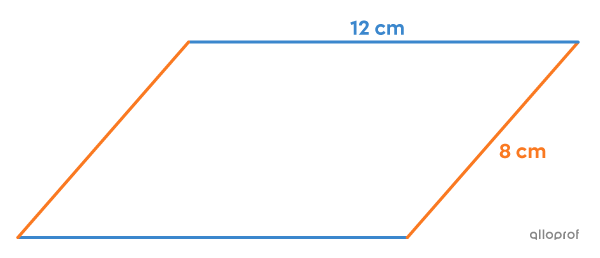
The measure of the base can be found as follows:
||\begin{align}y^2-4&=(\pm\, 4)^2-4\\&=16-4\\&=12\ \text{cm}\end{align}||
The measure of the orange sides can be found as follows:
||\begin{align}x^2-17&=(\pm\, 5)^2-17\\&=25-17\\&=8\ \text{cm}\end{align}||
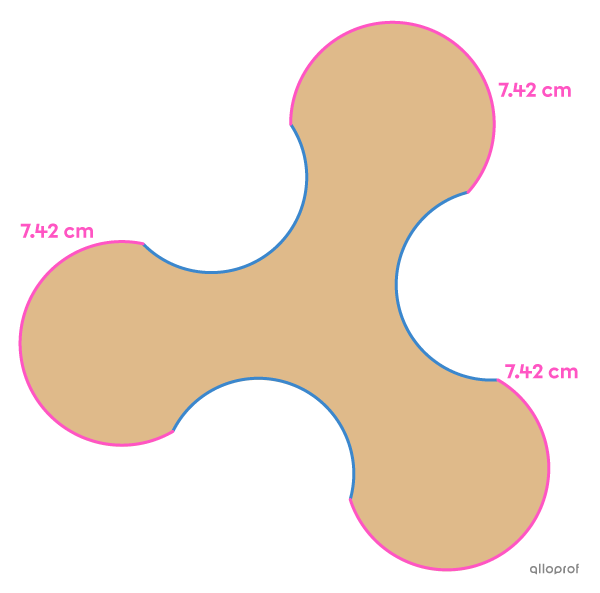
In an experimental setting, a company is trying to develop a new type of boomerang. To prevent people from getting hurt, a rubber band is installed around each end.

What is the necessary length of rubber if we know that:
-
the arcs of the same colour are congruent to one another;
-
the perimeter of the toy is |38.16\ \text{cm};|
-
a convex arc of the circle is |1.4| times longer than a concave arc of a circle?
-
Create a system of equations
1st equation
The 1st equation is created using the perimeter.
||\begin{align}P&= \text{Sum of the arcs of the circle}\\ 38.16&= 3x+3y\end{align}||
2nd equation
The 2nd equation is created using the fact that a convex arc of the circle is |1.4| times longer than a concave arc of a circle.
||\begin{align}\text{Convex arc} &= 1.4 \times \text{Concave arc}\\ x&=1.4y\end{align}||
-
Solve the system of equations
Using the substitution method, we get the following equation and we solve it.
||\begin{align}38.16 &=3\color{#3a9a38}x+3y\\ 38.16&=3(\color{#3a9a38}{1.4y})+3y\\ 38.16&=7.2y\\ 5.3&= y\end{align}||
We find the |x| value by substituting |y| with |5.3| in one of the initial equations.
||\begin{align}x&=1.4y\\ x&=1.4 (5.3)\\ x&= 7.42\end{align}||
-
Answer the question
Since there are 3 convex arcs, we find that the length of rubber needed is |3 \times 7.42,| so |22.26\ \text{cm}.|
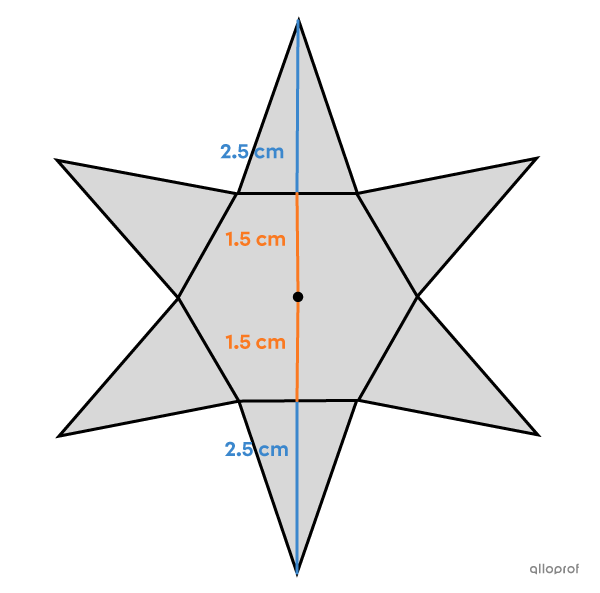
For a Halloween party, a student decides to wear a ninja costume. In order not to break any school rules, he must make sure that his accessories are no longer than |10\ \text{cm}.|
To add authenticity to his costume, he decides to make a cardboard shuriken.
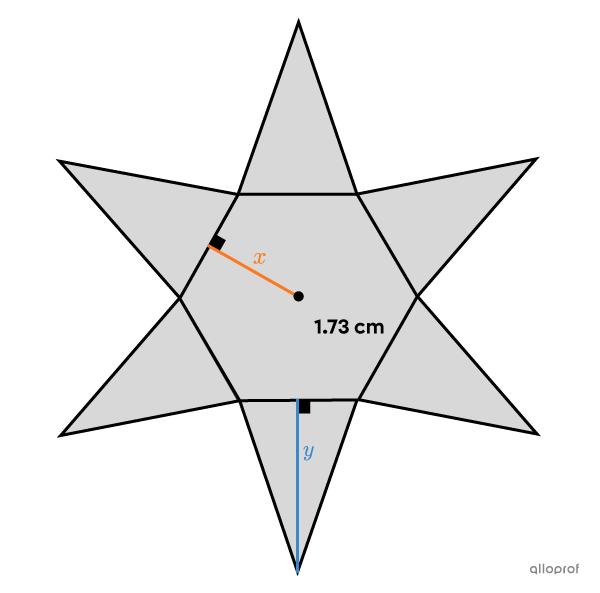
According to his calculations, his stars should meet the following constraints.
-
Each star is formed by a regular hexagon encased by 6 congruent isosceles triangles.
-
The total area of each star is |20.74\ \text{cm}^2.|
-
The measure of the height of a triangle exceeds that of the apothem by |1\ \text{cm}.|
Based on this information, do the stars comply with school regulations?
-
Construct a system of 2 equations
1st equation
The 1st equation is created using the total area of a star.
||\begin{align}A_\text{total}&=A_\text{hexagon}+6\times A_\text{triangle}\\ 20.74&=\dfrac{s\times a\times n}{2}+6 \left(\dfrac{b\times h}{2}\right)\\ 20.74&=\dfrac{1.73 \times x \times 6}{2}+6\left(\dfrac{1.73 \times y}{2}\right)\\ 20.74&=5.19x+5.19y\end{align}||
2nd equation
The 2nd equation is created using the fact that the measure of the height of a triangle exceeds that of the apothem by |1\ \text{cm}.|
||y=x+1||
-
Solve the system of equations
Using the substitution method, we get the following equation and solve it.
||\begin{align}20.74&=5.19x+5.19\color{#3a9a38}{y}\\ 20.74&=5.19x+5.19\color{#3a9a38}{(x+1)}\\ 20.74&=5.19x+5.19x+5.19\\ 15.55&=10.38x\\ 1.5&\approx x\end{align}||
We find the |y| value by substituting |x| with |1.5| in either of the initial equations.
||\begin{align}y&=\color{#3a9a38}x+1\\&=\color{#3a9a38}{1.5}+1\\&=2.5\end{align}||
-
Answer the question
It is okay to bring his shuriken to school since its length is |2.5+1.5+1.5+2.5 = 8\ \text{cm},| which does not exceed |10\ \text{cm}.|