In cases where the perimeter of a figure is known, one or more missing measurements may be sought. To solve problems related to perimeter, it is useful to know the perimeter formulas for different plane figures. Here are the steps to follow to find a missing measurement.
-
Determine the formula.
-
Replace the variables by the known values.
-
Isolate the unknown variable.
-
Answer the question.
Here are a series of examples. The first are geometry problems that have no particular context, while the last is a word problem that has a short scenario.
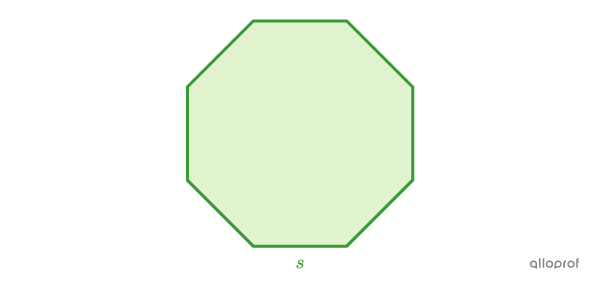
What is the measure of one side of a regular octagon with a perimeter of |28\ \text{cm}|?
-
Determine the formula.
Use the formula for the perimeter of a regular polygon.
||\begin{align}P&= \text{Sum of all sides}\\ &=8 \times s\end{align}|| -
Replace the variables by the known values.
||\begin{align} \color{#3a9a38}{P}&= 8s\\ \color{#3a9a38}{28}&=8s \end{align}|| -
Isolate the unknown variable.
We isolate |s| using the balancing equations method.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{28}}{8}}&=\color{#ec0000}{\dfrac{\color{black}{8s}}{8}}\\ 3.5 &=s\end{align}|| -
Answer the question.
One side of the regular octagon measures |3.5\ \text{cm}.|
What is the measure of the circle's radius if its circumference is |110\ \text{cm}|?

-
Determine the formula
Use the formula for the circumference of a circle.
||C= 2 \pi r|| -
Replace the variables by the known values.
||\begin{align}\color{#3a9a38}C&=2\pi r\\\color{#3a9a38}{110} &=2\pi r\end{align}|| -
Isolate the unknown variable.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{110}}{2\pi}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{2\pi}}\\ 17.51&\approx r \end{align}|| -
Answer the question.
The radius measures around |17.51\ \text{cm}.|
In the next examples, there are several missing measurements. Therefore, we must use algebraic expressions to represent the side measures.
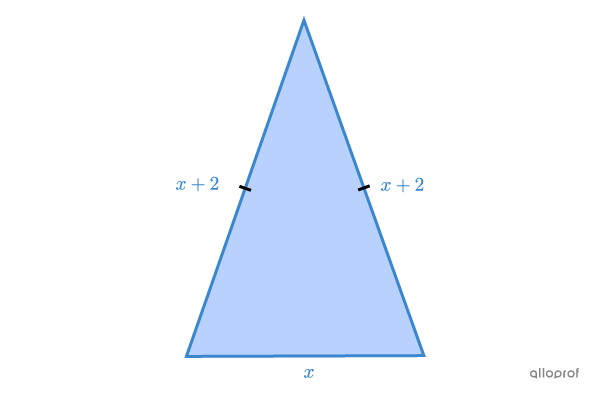
What are the side measures of an isosceles triangle that has a perimeter of |16\ \text{cm}| and whose congruent sides are 2 units more than its 3rd side?
-
Determine the formula.
Use the formula for the perimeter of a triangle.
||P= \text{Sum of all sides}|| -
Replace the variables by the known values.
Several pieces of information are missing. We can sketch a diagram to help find the measure of the sides using algebra. Let |x| represent the measure of the 3rd side, since it is the side for which we have the least information. Therefore, the algebraic expression that represents the measure of the 2 congruent sides is |x+2.|
Substituting this information into the perimeter formula, we get this:
||16=x+(x+2)+(x+2)||
-
Isolate the unknown variable.
Collect the like terms and isolate |x.|
||\begin{align}16&=\color{#3a9a38}x+\color{#3a9a38}x+\color{#3b87cd}2+\color{#3a9a38}x+\color{#3b87cd}2\\16&=\color{#3a9a38}{3x}+\color{#3b87cd}4\\16\color{#ec0000}{-4}&=3x+4\color{#ec0000}{-4}\\12&=3x\\\color{#ec0000}{\dfrac{\color{black}{12}}{3}}&=\color{#ec0000}{\dfrac{\color{black}{3x}}{3}}\\4&=x\end{align}|| -
Answer the question.
The congruent sides measure |6\ \text{cm},| because |x+2=4+2=6,| and the 3rd side measures |4\ \text{cm}.|
What are the side measures of a rectangle that has a perimeter of |192\ \text{cm}| and whose length measures three times the width?
-
Determine the formula.
Use the formula for the perimeter of a rectangle.
||P= \text{Sum of all sides}|| -
Replace the variables with the known values.
Several pieces of information are missing. We can sketch a diagram to help us find the measure of the sides using algebra. We assign |x| to the measure of the width, since we have less information about this side. Therefore, the algebraic expression that represents the length is |3x.|

Substituting this information into the perimeter formula, we get:
||192=x+x+(3x)+(3x)||
-
Isolate the unknown variable.
||\begin{align}192&=x+x+3x+3x\\192&=8x\\\color{#ec0000}{\dfrac{\color{black}{192}}{8}}&=\color{#ec0000}{\dfrac{\color{black}{8x}}{8}}\\24&=x\end{align}|| -
Answer the question.
The width measures |24\ \text{cm},| while the length measures |72\ \text{cm}| |(3x = 3\times 24=72).|
The Cycling Grand Prix, which has been held for the past few years in Quebec City and Montreal, requires organizers to create new routes while respecting certain constraints.
This year, the race circuit must be |15\ 000\ \text{m}| long and must consist of different sections, including a climb, a descent and a straight line for the final sprint.
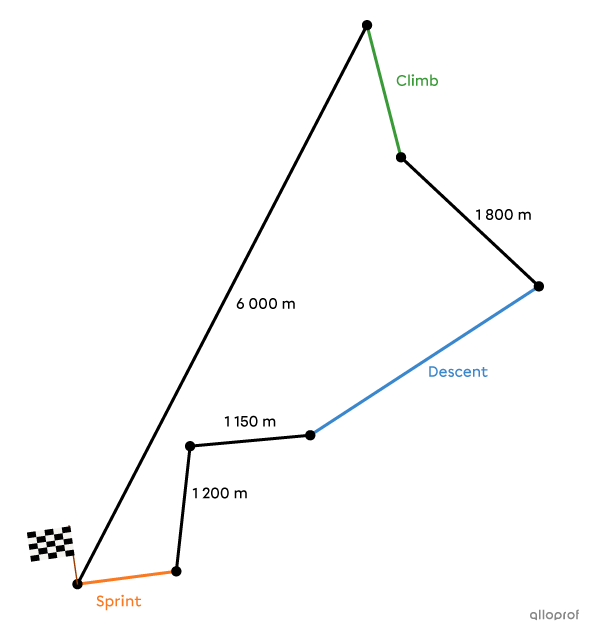
To respect the standards between races, the descent must be twice as long as the climb and the straight line for the sprint must be |300\ \text{m}| longer than half the climb.
What is the travelling distance for each of these 3 sections?
-
Determine the formula.
The total length of the course circuit is known.
||\text{Length of the circuit}=\text{Sum of all segments}||
-
Replace the variables with the known values.
Several pieces of information are missing. We can use the image to help us find the length of the climb, descent and sprint using algebra. We write that |\color{#3a9a38}x| is the length of the climb. So, the algebraic expression that represents the descent is |\color{#3b87cd}{2x}| and the expression which represents the sprint is |\color{#fa7921}{\dfrac{x}{2}+300}.|
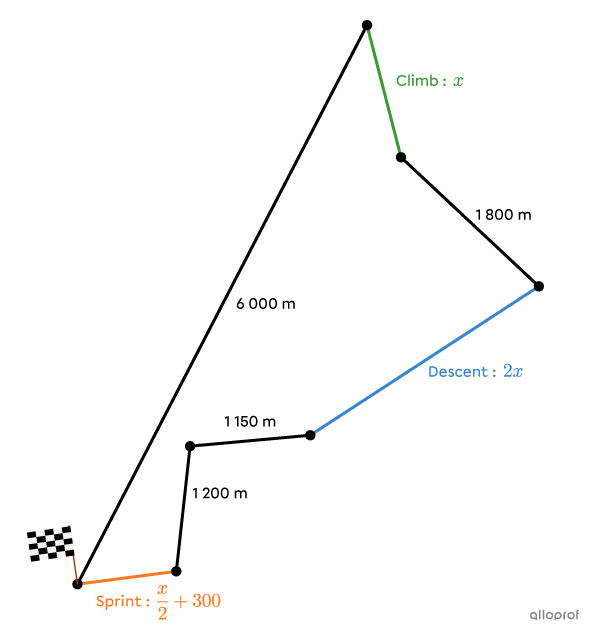
Substituting this information into the total length of the circuit formula, we get:
||15\ 000=6\ 000+x+1\ 800+2x+1\ 150+1\ 200+\left(\dfrac{x}{2}+300\right)||
-
Isolate the unknown variable.
||\begin{align}15\ 000&=6\ 000+x+1\ 800+2x+1\ 150+1\ 200+\dfrac{x}{2}+300\\15\ 000&=\dfrac{7x}{2}+10\ 450\\15\ 000\color{#ec0000}{-10\ 450}&=\dfrac{7x}{2}+10\ 450\color{#ec0000}{-10\ 450}\\4\ 550&=\dfrac{7x}{2}\\4\ 550\color{#ec0000}{\times 2}&=\dfrac{7x}{2}\color{#ec0000}{\times 2}\\9\ 100&=7x\\\color{#ec0000}{\dfrac{\color{black}{9\ 100}}{7}}&=\color{#ec0000}{\dfrac{\color{black}{7x}}{7}}\\1\ 300&=x\end{align}||
-
Answer the question.
So, the climb's length is |1\ 300\ \text{m},| the descent's length is |2\ 600\ \text{m}| |(2x= 2\times 1\ 300=2\ 600)| and the sprint's length is |950\ \text{m}| |\left(\dfrac{x}{2}+300=\dfrac{1\ 300}{2}+300=950\right).|

Pour valider ta compréhension des mesures manquantes dans les figures planes de façon interactive, consulte la MiniRécup suivante :
