We often have to find missing measurements in plane figures. Sometimes, solving such problems creates a 2nd degree (quadratic) equation or a system of equations.
To solve them, we must use the quadratic formula or factoring. You also need to know the area and perimeter formulas. Here are the steps to follow to do so.
-
Construct an equation or a system of equations from the context.
-
Solve the equation or the system of equations.
-
Answer the question.
Here are a series of examples. The first ones are geometry problems that do not have a specific context, while the last one is a word problem that presents a short scenario.
Find the measure of each side of the following isosceles triangle if its perimeter is |100\ \text{cm}.|
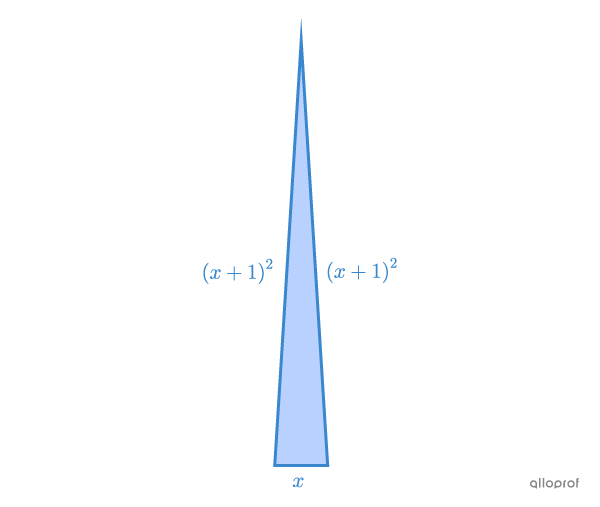
-
Construct an equation from the context
We will use the perimeter of a triangle formula.
||\begin{align}P&= \text{Sum of all sides} \\ 100 &= x + (x+1)^2 + (x+1)^2 \\ 100 &= x + x^2+2x + 1 +x^2 + 2x + 1\\ 100 &= 2x^2 +5x+2 \end{align}|| -
Solve the equation
Since this is a 2nd degree (quadratic) equation, we will place all terms on the same side of the equation so that we can solve it using the quadratic formula.
||\begin{align}100&=2x^2+5x+2\\0&=2x^2+5x-98\\\\x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(5)\pm\sqrt{(5)^2-4(2)(-98)}}{2(2)} \\&=\dfrac{-5\pm\sqrt{809}}{4}\end{align}\\\begin{aligned}\\x_1&=\dfrac{-5-\sqrt{809}}{4}&x_2&=\dfrac{-5+\sqrt{809}}{4}\\x_1&\approx-8.36&x_2&\approx5.86\end{aligned}||
Since we are looking for a length, we reject |x_1\approx-8.36,| since its value is negative. Therefore we have |x\approx5.86\ \text{cm}.|
-
Answer the question
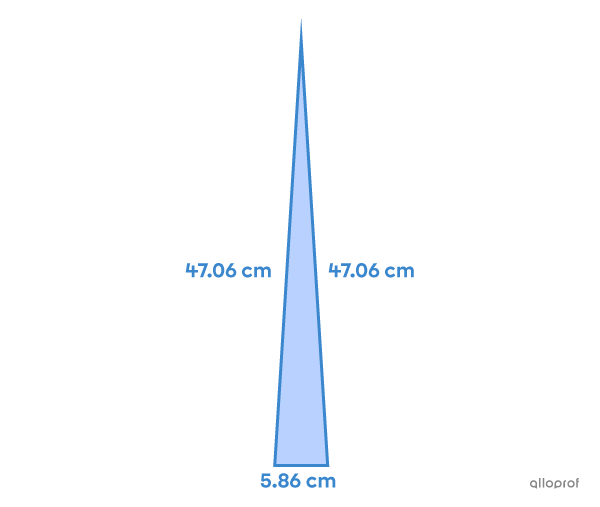
The congruent sides measure approximately |47.06\ \text{cm},| since |(x+1)^2 = (5.86+1)^2 \approx 47.06.| The measure of the 3rd side is about |5.86\ \text{cm},| since |x\approx 5.86.|
Find the measure of the rectangle’s sides if its area is |15\ \text{m}^2.|
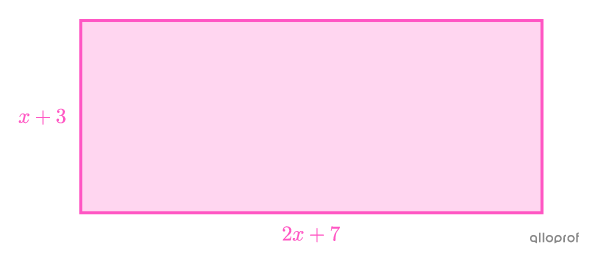
-
Construct an equation from the context
Use the formula for the area of a rectangle.
||\begin{align}A&=b\times h \\ 15&=(2x+7)(x+3)\\ 15&=2x^2+6x+7x+21\\ 15&=2x^2+13x+21\end{align}|| -
Solve the equation
Since this is a 2nd degree (quadratic) equation, we will place all terms on the same side of the equation so that we can solve it. To do so, we will use the product-sum method.
||\begin{align}15&=2x^2+13x+21\\0&=2x^2+13x+6\end{align}||
We are looking for 2 numbers that have a product of |2\times 6 = 12| and whose sum is |13.| The numbers are |1| and |12.|
||\begin{align}0&=2x^2+\color{#3a9a38}{13x}+6\\0&=2x^2+\color{#3a9a38}{x+12x}+6\\ 0&=x(2x+1)+6(2x+1)\\ 0&=(2x+1)(x+6) \end{align}\\ \begin{aligned}\\0&=2x+1&0&=x+6\\-1&=2x&-6&=x_2\\-0.5&=x_1\end{aligned}||
We must reject |x_2=-6,| since this |x| value would imply that the measure of the sides is negative, which is impossible.
-
Answer the question
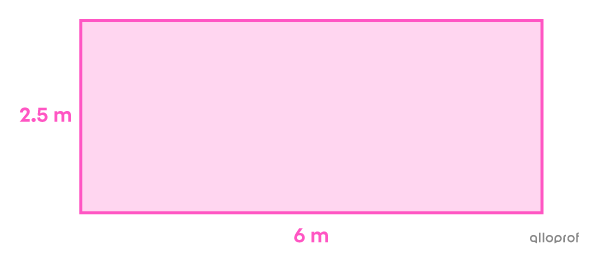
The base measures |6\ \text{m},| since |2x+7=2(-0.5)+7 =6.| The height is |2.5\ \text{m},| since |x+3=-0.5+3 =2.5.|
What are the measures of the legs of the triangle if its perimeter is |38.4\ \text{cm}| and its area is |61.44\ \text{cm}^2?|
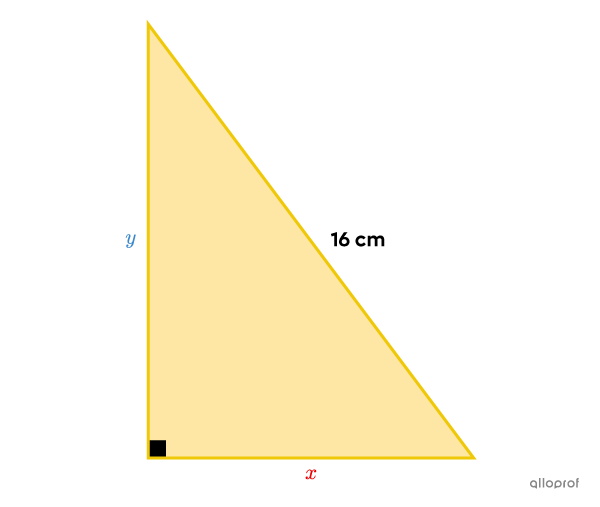
-
Construct a system of equations from the context
Since there are 2 unknowns, we must make 2 equations. To do so, we will use the perimeter and the area of the triangle.
||\begin{align} P&= \text{Sum of all sides}\\ 38.4&= \color{#ec0000}x + \color{#3b87cd}{y}+16 \\22.4&= x + y\end{align}||
||\begin{align} A&= \dfrac{\color{#ec0000}b\times \color{#3b87cd}h}{2}\\61.44&= \dfrac{\color{#ec0000}x \times \color{#3b87cd}{y}}{2} \\122.88&= x\times y\end{align}||
-
Solve the system of equations
We can isolate |y| in the 1st equation and substitute it into the 2nd equation.
||\begin{align} 22.4&=x+y\\22.4-x&=y\\\\122.88&=x\times \color{#ec0000}y\\122.88&=x\times \color{#ec0000}{(22.4-x)}\\122.88&=22.4x-x^2\\ 0&=-x^2+22.4x-122.88\end{align}||
Since it is a 2nd degree (quadratic) equation, we can use the quadratic formula to solve it.
||\begin{align}x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(22.4) \pm \sqrt{(22.4)^2-4(-1)(-122.88)}}{2(-1)}\\&=\dfrac{-22.4\pm \sqrt{10.24}}{-2}\end{align}\\\begin{aligned}\\x_1&=\dfrac{-22.4- \sqrt{10.24}}{-2}& x_2&=\dfrac{-22.4+ \sqrt{10.24}}{-2}\\ &= 12.8 &&= 9.6\end{aligned}||
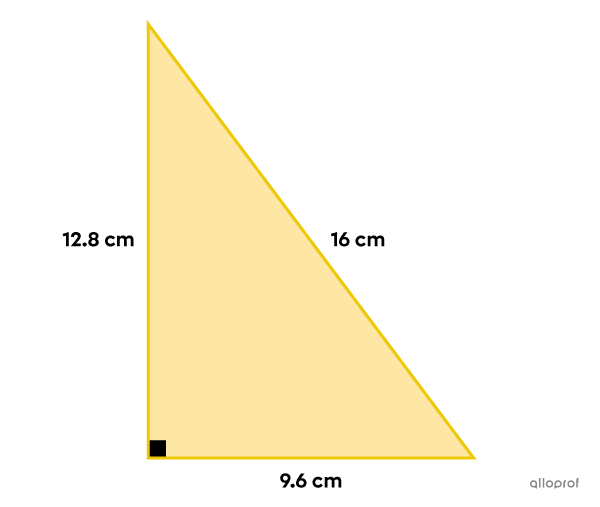
Both values are valid. They each respectively represent the measure of the legs. We assume that |x| is the shorter leg, so |x=9.6\ \text{cm}| and |y=12.8\ \text{cm}.|
-
Answer the question
The short leg measures |9.6\ \text{cm}| and the long leg measures |12.8\ \text{cm}.|
Find the total height of this figure using the following information:
-
The height of the rectangle measures |3\ \text{dm}| more than its base.
-
The measure of the diameter of the half-circle is triple the measure of the rectangle’s base.
-
The total area of this figure is |84.55\ \text{dm}^2.|
-
Construct an equation from the context
Since there is no information about the base of the rectangle, we set its measure as the variable |x.|
|x :| base of the rectangle
The height is |3\ \text{dm}| longer than the base, so the algebraic expression that represents it is |x+3.|
The diameter of the half-circle is triple the base of the rectangle, so it can be represented by the algebraic expression |3x.|
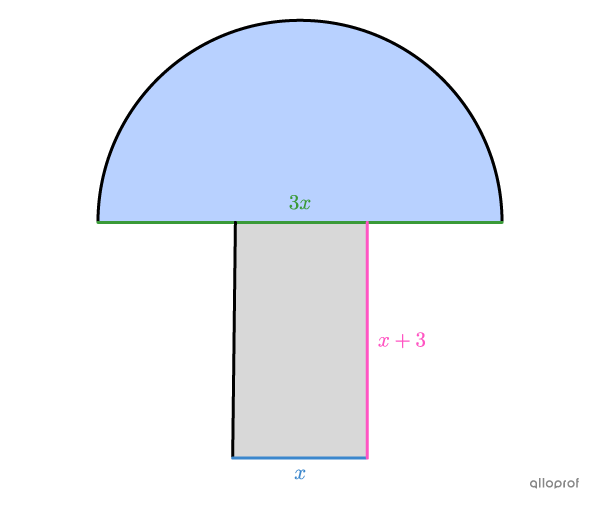
We use the total area of a decomposable figure to construct the equation. The figure is composed of a half-circle and a rectangle. We therefore find the following equation:
||\begin{align} A_\text{total} &= A_\text{rectangle} + A_\text{half-circle}\\A_\text{total} &= bh + \dfrac{\pi r^2}{2}\\ 84.55 &=\color{#3b87cd}x (\color{#ff55c3}{x+3}) + \dfrac{\pi \left(\dfrac{\color{#3a9a38}{3x}}{2}\right)^2}{2}\\ 84.55 &\approx x^2+3x+3.53x^2\\84.55&\approx4.53x^2+3x \end{align}||
-
Solve the equation
Since it is a 2nd degree (quadratic) equation, we put all the terms on one side of the equation to solve it using the quadratic formula.
||\begin{align}84.55&\approx4.53x^2+3x\\ 0&\approx4.53x^2+3x-84.55\\\\x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(3) \pm \sqrt{(3)^2-4(4.53)(-84.55)}}{2(4.53)}\\&=\dfrac{-3\pm \sqrt{1\ 541.046}}{9.06}\end{align}\\ \begin{aligned}\\x_1&=\dfrac{-3- \sqrt{1\ 541.046}}{9.06}& x_2&=\dfrac{-3+ \sqrt{1\ 541.046}}{9.06}\\ &\approx -4.66 &&\approx 4\end{aligned}||
Since we are looking for a length, we reject |x_1\approx-4.66,| since it is a negative value. Therefore, we have |x\approx 4\ \text{dm}.| -
Answer the question
The total height of the figure is found using the height of the rectangle and the radius of the half-circle.
||\begin{align}\begin{aligned}\color{#ff55c3}{h_{\text{rectangle}}}&=x+3\\[10pt]&=4+3\\[10pt]&=7\ \text{dm}\\[-2pt]\\ \end{aligned}\quad \begin{aligned}\color{#3a9a38}{r_{\text{half-circle}}}&=\dfrac{3x}{2}\\&=\dfrac{3(4)}{2}\\&=\dfrac{12}{2}\\&=6\ \text{dm}\end{aligned}\end{align}||
||\begin{align}h_{\text{total}}&=\color{#ff55c3}{h_{\text{rectangle}}}+\color{#3a9a38}{r_{\text{half-circle}}}\\&=7\ \text{dm}+6\ \text{dm}\\&=13\ \text{dm}\end{align}||
The total height of the figure is |13\ \text{dm}.|

With the opening of his new business, the owner of an ice cream shop wants to buy an advertising poster.
However, his budget limits him to the following constraints:
-
The area of the half-circle and the ice cream rim should be equal to |253\ \text{cm}^2.|
-
The area of the ice cream cone drawing and the rim of the ice cream should be equivalent to |276\ \text{cm}^2.|
-
The height of the cone must be |18\ \text{cm}.|
-
The height of the ice cream rim must be |4\ \text{cm}.|
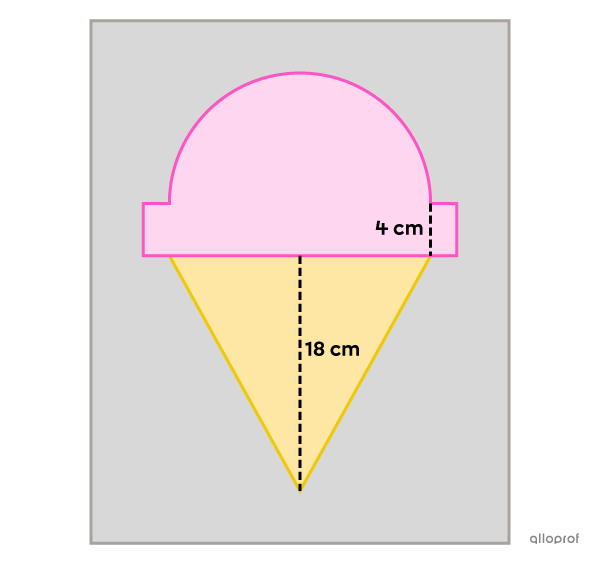
What must be the dimensions of the poster if the poster extends |4\ \text{cm}| beyond each end of the drawing?
-
Construct a system of equations from the context
To determine the dimensions of the poster, we need to find the length of the rim and the radius of the half-circle.
|x :| Radius of the half-circle
|y :| Length of the rim
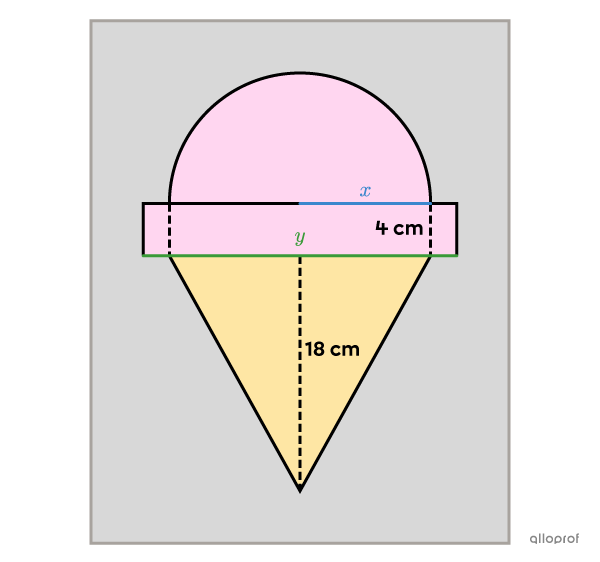
Since we have 2 pieces of information about the area, it is possible to create 2 equations.
||\begin{align}253&=A_{\text{half-circle}}+A_{\text{rim}}\\ 253&=\dfrac{\pi\color{#3b87cd}x^2}{2}+4\color{#3a9a38}y\\506&=\pi x^2+8y\end{align}||
||\begin{align}276&=A_{\text{triangle}}+A_{\text{rim}}\\276&=\dfrac{2\color{#3b87cd}x\times 18}{2}+4\color{#3a9a38}y\\276&=18x+4y\end{align}||
-
Solve the system of equations
To solve this system of equations, we can multiply the 2nd equation by |2| and use the elimination method.
||\begin{align}\color{#ec0000}{2\times \big(}276&=18x+4y\color{#ec0000}{\big)}\\552&=36x+8y\end{align}||
We subtract the 2nd equation from the 1st.
||\begin{align}506&=\pi x^2\ \ \phantom{+36x} +8y\\ -\ (552&=\ \ \phantom{\pi x^2+} 36x+8y)\\\hline-46&=\pi x^2-36x+0y\end{align}||
We use the quadratic formula to solve this 2nd degree equation.
||\begin{align}-46&=\pi x^2-36x\\ 0&=\pi x^2-36x+46\\\\x&=\dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\&= \dfrac{-(-36) \pm \sqrt{(-36)^2-4(\pi)(46)}}{2\pi}\\ &\approx\dfrac{36\pm \sqrt{717.95}}{6.28}\end{align}\\\begin{aligned}\\x_1&\approx\dfrac{36- \sqrt{717.95}}{6.28}& x_2&\approx\dfrac{36+ \sqrt{717.95}}{6.28}\\ &\approx 1.47 &&\approx 10\end{aligned}||
Both answers are valid and meet the criteria. For the rest of the problem, we will choose |\color{#3b87cd}{x_2 \approx 10}| so that the form of the ice cream cone is more realistic. Next, we can find the value of |y| by replacing |x| with |10| in one of the preceding equations.
||\begin{align}276 &= 18\color{#3b87cd}x + 4y\\ 276 &= 18(\color{#3b87cd}{10}) + 4y \\276&=180+4y\\96&=4y\\ 24&=y\end{align}||
-
Answer the question
All that is left is to calculate the dimensions of the poster.
For the width, we use |y.|
||\begin{align}\text{Width}&=4+y+4\\&=4+24+4\\&=32\ \text{cm}\end{align}||
For the length, we use |x.|
||\begin{align}\text{Length}&=4+18+4+x+4\\&=4+18+4+10+4\\&=40\ \text{cm}\end{align}||
The poster must have a width of |32\ \text{cm}| and a length of |40\ \text{cm}.|
