Tree diagrams are very useful in probability. There are two variations of tree diagrams: those that represent and enumerate (or list) all the possible outcomes in the sample space, and those that represent and calculate the probability of each outcome.
A tree diagram is a visual representation of all the possible outcomes of a multi-step random experiment.
A coin and a |6|-sided die are tossed at the same time. How many possible outcomes are there?
We start with the 1st coin toss. The possible outcomes are heads (H) or tails (T). So, |2| branches are drawn like this.
We continue with the 2nd toss of the die. The possible outcomes of rolling a |6|-sided die are: 1, 2, 3, 4, 5 and 6. We therefore draw |6| branches at the end of each of the 2 branches from the 1st toss. To finish, the possible outcomes are written in brackets in a column on the right.

By counting the possible outcomes one by one, there are |12| possible outcomes. We can also use the multiplication rule, since each of the |2| branches of the first toss generated |6| branches. There are therefore |2\times 6=12| possible outcomes.
The tree diagram should not branch in all directions. The results of each step of the random experiment should be vertically aligned (in one column to the right of the previous step). If needed, add the Outcomes column completely to the right.

If the random experiment is composed of simple events that are equiprobable, then, after enumerating all possible outcomes with the help of a tree diagram, probability questions can be answered.
What is the probability of getting tails at least 2 times in a row if you toss 3 coins successively?
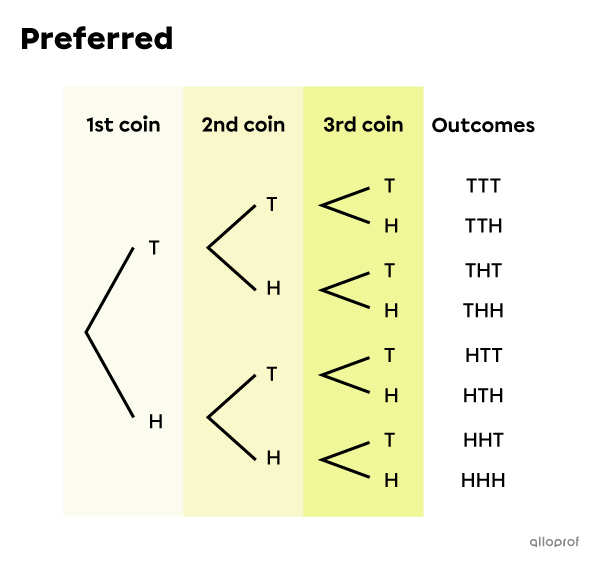
We start by making the tree diagram where we represent the outcome Tails by the letter T and the outcome Heads by the letter H.
This is a 3-step random experiment with replacement where the order matters, since 3 coins are thrown successively, each with a heads and tails side.
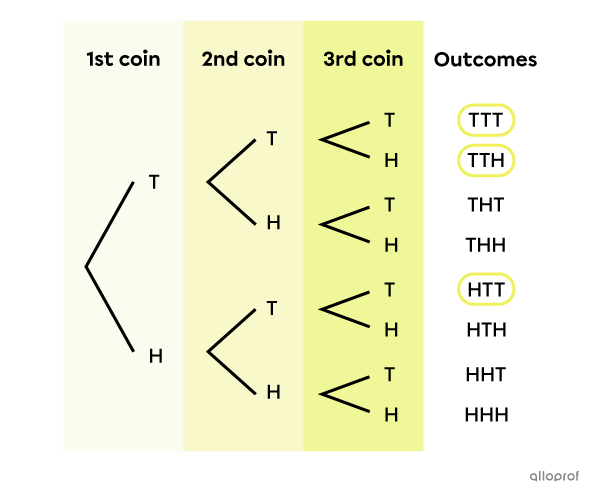
Note that there are 8 possible outcomes: TTT, TTH, THT, THH, HTT, HTH, HHT, and HHH. These 8 results are all equiprobable, because the theoretical probability of getting heads is always equal to the probability of getting tails.
Of these 8 cases, 3 have at least 2 instances of tails in a row: TTT, TTH and HTT.
Since there are 3 favourable outcomes to the event "getting tails at least 2 times in a row" and all possible outcomes are equiprobable, we get the following probability:
||\begin{align}P\left(\begin{gathered}\text{Getting Heads}\\ \text{2 Times in a Row}\end{gathered}\right)&=\dfrac{\text{Number of Favourable Outcomes}}{\text{Number of Possible Outcomes}}\\ &=\dfrac{3}{8}\end{align}||
Answer: The probability of getting tails at least 2 times in a row is |\dfrac{3}{8}.|
In a tree diagram, each outcome is found only once, even though some outcomes have a higher probability of occurring than others. For example, if you draw 2 marbles from a bag containing 2 black marbles (B) and 1 white marble (W), you should get the 1st diagram below, which shows 4 possible outcomes.
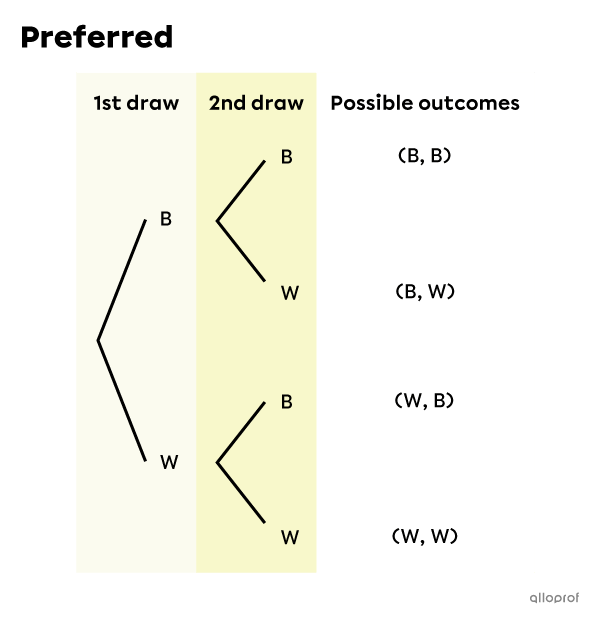
There are therefore 4 possible outcomes, even if they are not all equiprobable. For the moment, we cannot answer probability questions until we transform this tree diagram to one that also includes probabilities, referred to as a probability tree.
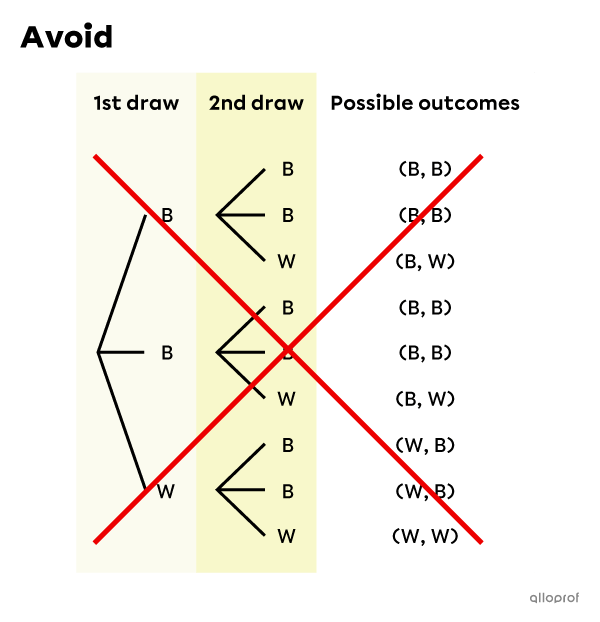
This diagram is confusing, because it looks like there are 9 possible outcomes, but there are only 4 different ones. In other words, there are unnecessary branches drawn.
The probability tree is a tree diagram where each branch of a multi-step random experiment has its probabilities included.
Une erreur s’est glissée dans cette vidéo.
À 2 min 31 s, on devrait entendre « R, B » et non « R, V ».
To answer probability questions using a probability tree, follow these steps:
-
Determine the possible outcomes.
-
Make a tree diagram.
-
Place the probabilities on the branches.
-
Calculate the probability of each outcome.
-
Calculate the probability sought.
There are 2 possible situations.
In the case of a random experiment with replacement, the probabilities written on each of the branches of the diagram are the same from one step to the next.
Romy cuts out all the letters of the word MISSISSIPPI and puts them in a bag. She draws a 1st letter at random, writes it down and puts it back in the bag. Then she draws a 2nd letter. Using the 2 letters she drew, she forms a 2-letter code. She wants to know the probability of her code consisting of 2 different letters.
-
Determine the possible outcomes
We start by making a tree diagram of the situation to represent all possible outcomes.
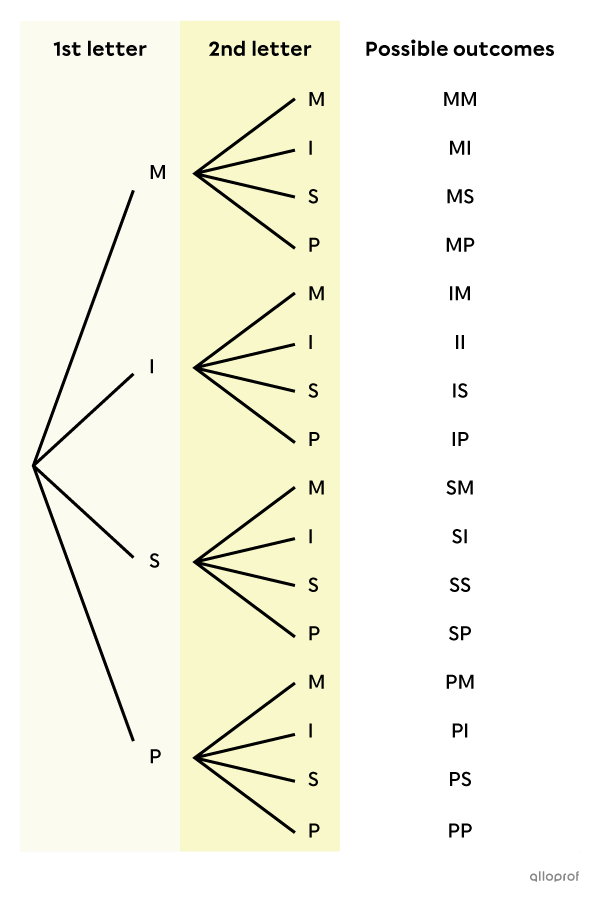
There are therefore |4\times 4=16| possible outcomes.
-
Make a tree diagram
The possibilities are the final outcomes of the experiment: MM, MI, MS, MP, IM, II, IS, IP, SM, SI, SS, SP, PM, PI, PS and PP. In the tree diagram, they are found in the column on the far right -
Place the probabilities on the branches
In the following probability tree, the probabilities associated with the first draw are the same as those associated with the second.
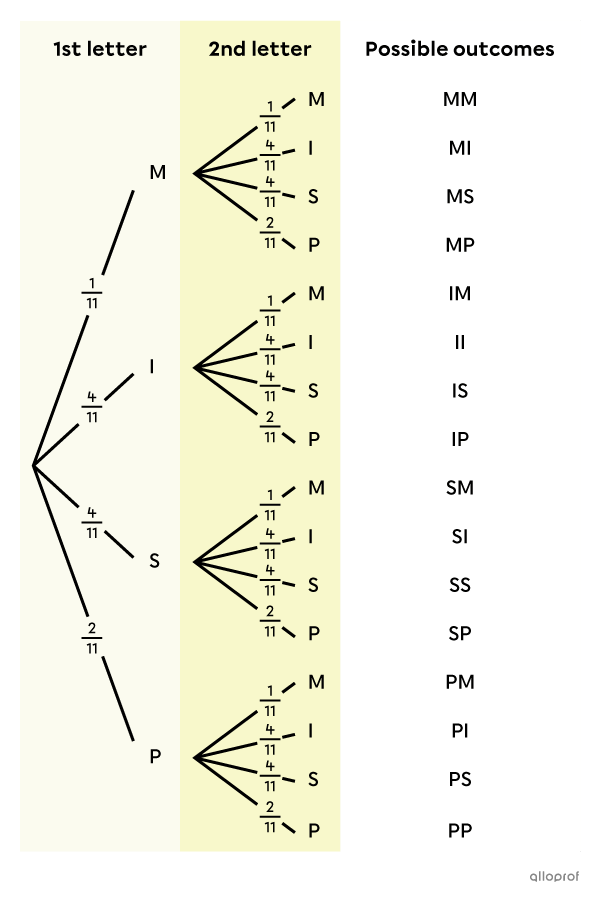
-
Calculate the probability of each outcome
To calculate the probability of each possible outcome, we use the multiplication rule: we calculate the product of the probabilities located on the branches that lead to the outcome. For example, for MM, we multiply |\dfrac{1}{11}\times \dfrac{1}{11},| for MI, we multiply |\dfrac{1}{11}\times \dfrac{4}{11},| and so on. The following complete probability tree is then obtained.
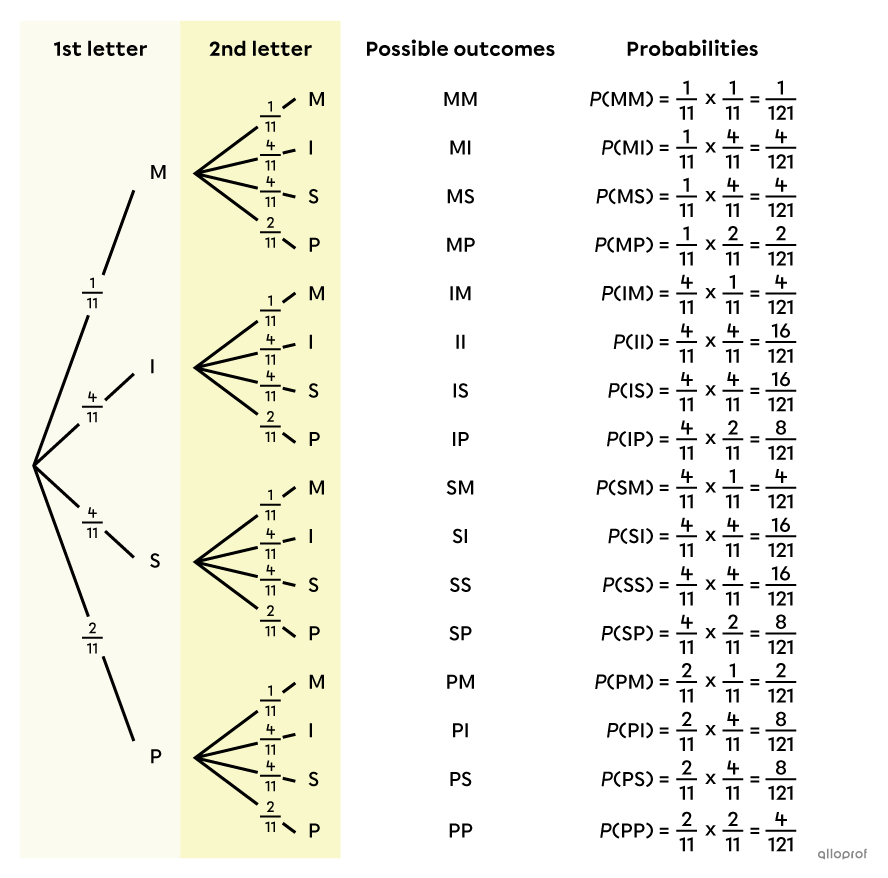
-
Calculate the probability sought.
Remember that Romy wants to know the probability of her code being composed of 2 different letters. This can be done by adding up the probability of all the favourable outcomes: MI, MS, MP, IM, IS, IP, SM, SI, SP, PM, PI and PS.
||\begin{align}P\left(\begin{gathered}\text{getting 2 different}\\ \text{letters}\end{gathered}\right) =\ &P(\text{MI})+P(\text{MS})+P(\text{MP})+P(\text{IM})+P(\text{IS})+P(\text{IP})\,+\\&P(\text{SM})+P(\text{SI})+P(\text{SP})+P(\text{PM})+P(\text{PI})+P(\text{PS})\\ =\ &\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{2}{121}+\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\\&\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\dfrac{2}{121}+\dfrac{8}{121}+\dfrac{8}{121}\\ =\ &\dfrac{84}{121}\end{align}||
Answer: The probability that Romy's code is composed of 2 different letters is |\dfrac{84}{121},| or about |69\ \%.|
The events "getting a code composed of 2 different letters" and "getting a code composed of 2 identical letters" are complementary events. Because the sum of the probabilities of two complementary events is always |1| or |100\%,| it is sometimes more efficient to calculate the probability of the complementary event and then subtract, rather than calculating the required probability. In the previous example, the final calculation would have been as follows:
||\begin{align}P(\text{getting 2 different letters})&=100\ \% -P(\text{getting 2 identical letters})\\ &=100\ \%-\big(P(\text{MM})+P(\text{II})+P(\text{SS}) + P(\text{PP})\big)\\&=\dfrac{121}{121}-\left(\dfrac{1}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{4}{121}\right)\\&=\dfrac{121}{121}-\dfrac{37}{121}\\&=\dfrac{84}{121}\end{align}||
In a probability tree, the sum of the probabilities of each cluster of branches must always equal |1| or |100\%.|
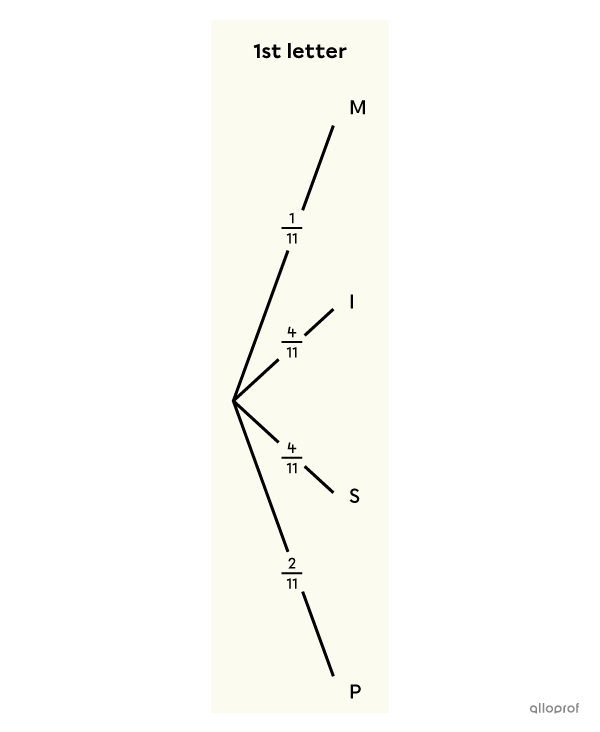
||\dfrac{1}{11}+\dfrac{4}{11}+\dfrac{4}{11}+\dfrac{2}{11}=\dfrac{11}{11}=1||
The sum of the probabilities of the 4 branches is indeed |100\ \%.| If it is not, it indicates that there is an error to correct.
The sum of the probabilities of all the possible outcomes of the tree should also equal |1| or |100\%.|
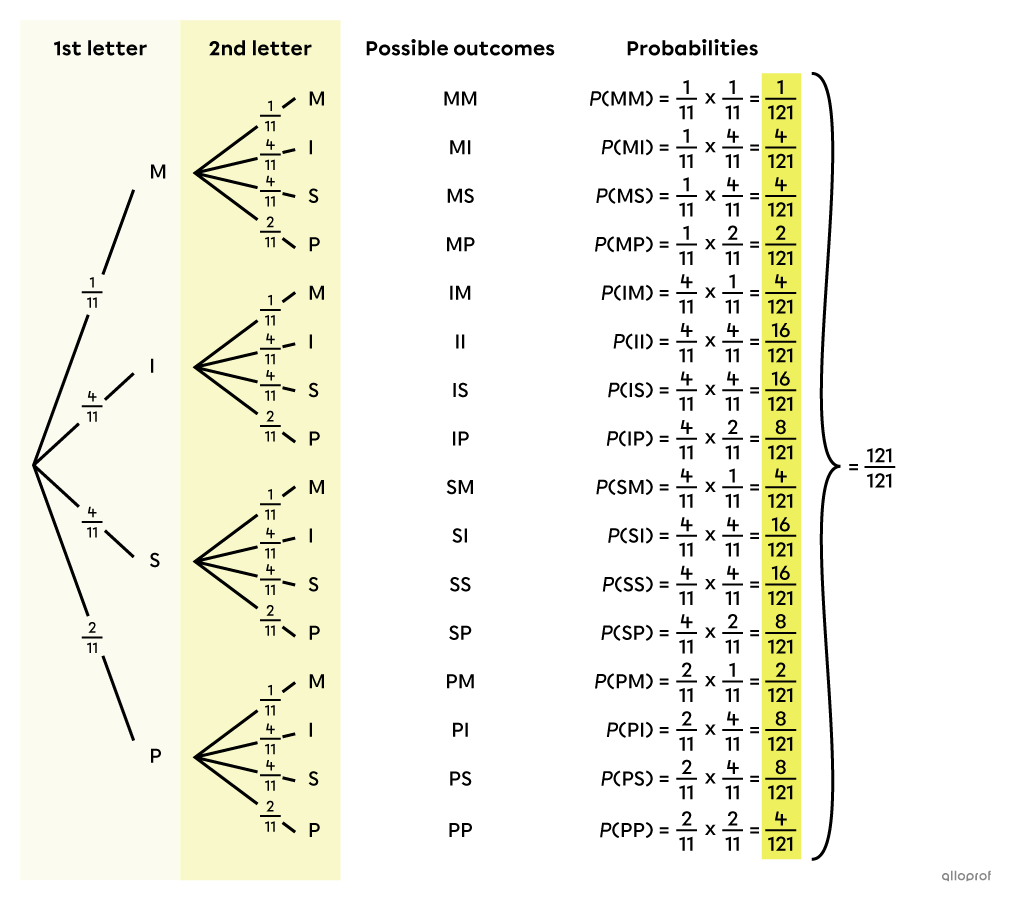
||\begin{align}\dfrac{1}{121}+\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{2}{121}+\dfrac{4}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{8}{121}\,&+\\ \dfrac{4}{121}+\dfrac{16}{121}+\dfrac{16}{121}+\dfrac{8}{121}+\dfrac{2}{121}+\dfrac{8}{121}+\dfrac{8}{121}+\dfrac{4}{121}&=\dfrac{121}{121}\end{align}||
The sum of all the probabilities is indeed |100\ \%.| If this is not the case, it is a sign that there is an error to correct.
For a random experiment without replacement, the probabilities on each of the branches of the diagram change from one step to the next.
Romy cuts out all the letters of the word MISSISSIPPI and puts them in a bag. She draws 2 letters at random to form a 2-letter code. She wants to know the probability that her code consists of 2 different letters.
-
Determine the possible outcomes
We start by making a tree diagram of the situation to represent all possible outcomes. Since both letters are drawn at the same time, this is a random experiment without replacement.
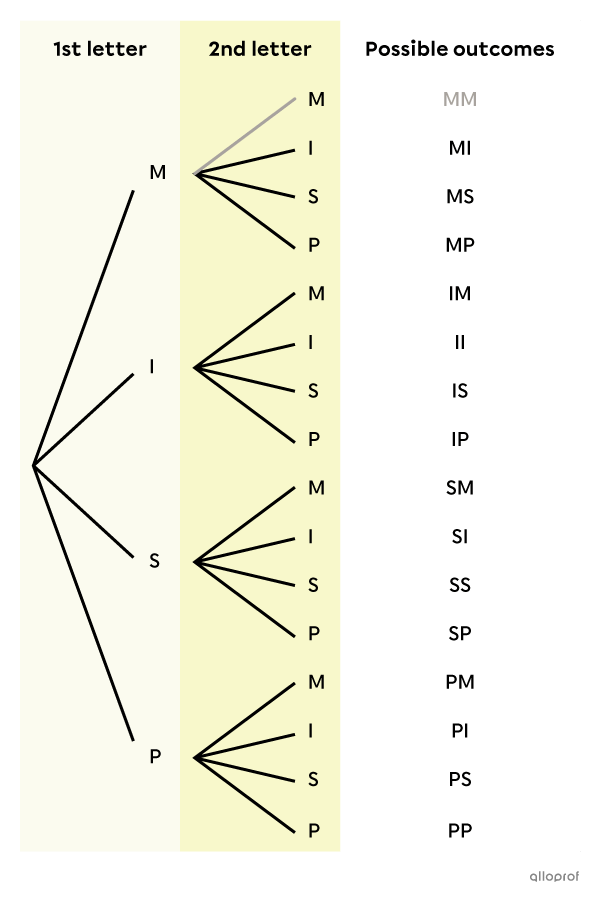
Therefore, there are |15| possible outcomes, since the outcome MM is impossible. There is only one letter M in the bag and it is a draw without replacement. We could therefore have decided not to put this branch in the diagram at all.
-
Make a tree diagram
The outcomes in the sample space are: MI, MS, MP, IM, II, IS, IP, SM, SI, SS, SP, PM, PI, PS and PP. -
Place the probabilities on the branches
The following probability tree is formed.
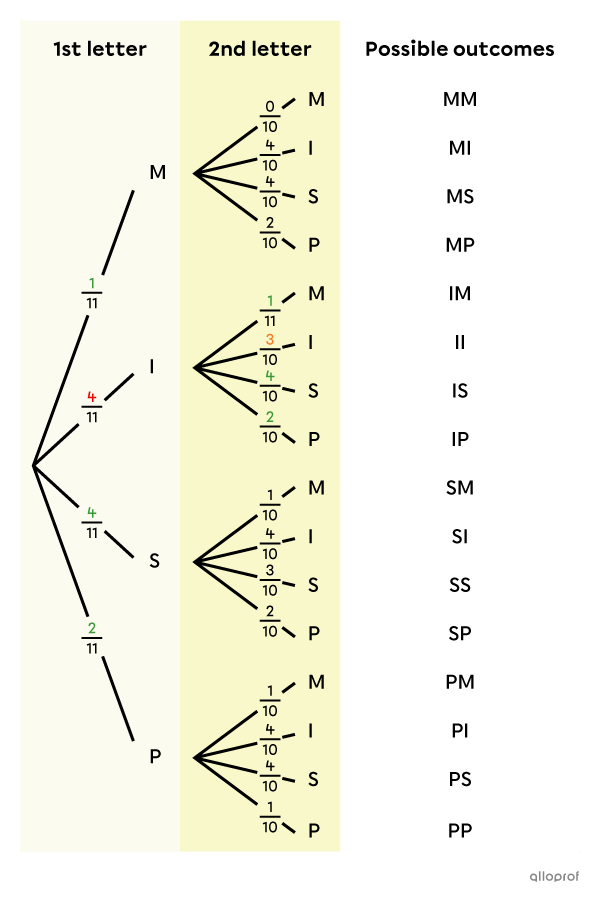
The denominator of the fractions associated with the 1st draw is 11, because there are 11 letters in the bag at the time of the 1st draw.
The fractions in the second draw are out of 10, because only 10 letters are left since the 1st drawn letter is not replaced in the bag.
The numerators do not change with the exception of the option chosen in the previous draw. For example, if you draw one of the 4 I's on the 1st draw, there are only 3 I's left for the 2nd draw.
Note:
For the outcome MM, the probability on the 2nd branch is |\dfrac{0}{10},| because no letter M is left in the bag.
For each cluster of branches in the 1st and 2nd draws, the sum of the probabilities is always |1.|
||\begin{align}\dfrac{1}{11}+\dfrac{4}{11}+\dfrac{4}{11}+\dfrac{2}{11}&=\dfrac{11}{11}\\\\ \dfrac{0}{10}+\dfrac{4}{10}+\dfrac{4}{10}+\dfrac{2}{10}&=\dfrac{10}{10}\\ \dfrac{1}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{2}{10}&=\dfrac{10}{10} \\ \dots\end{align}||
So we can move forward.
-
Calculate the probability of each outcome
To calculate the probability of each possible outcome, we use the multiplication rule: we calculate the product of the probabilities located on the branches that lead to the outcome. For example, for MM, we multiply |\dfrac{1}{11}\times \dfrac{0}{10},| for MI, we multiply |\dfrac{1}{11}\times \dfrac{4}{10},| and so on.
The following complete probability tree is then obtained.
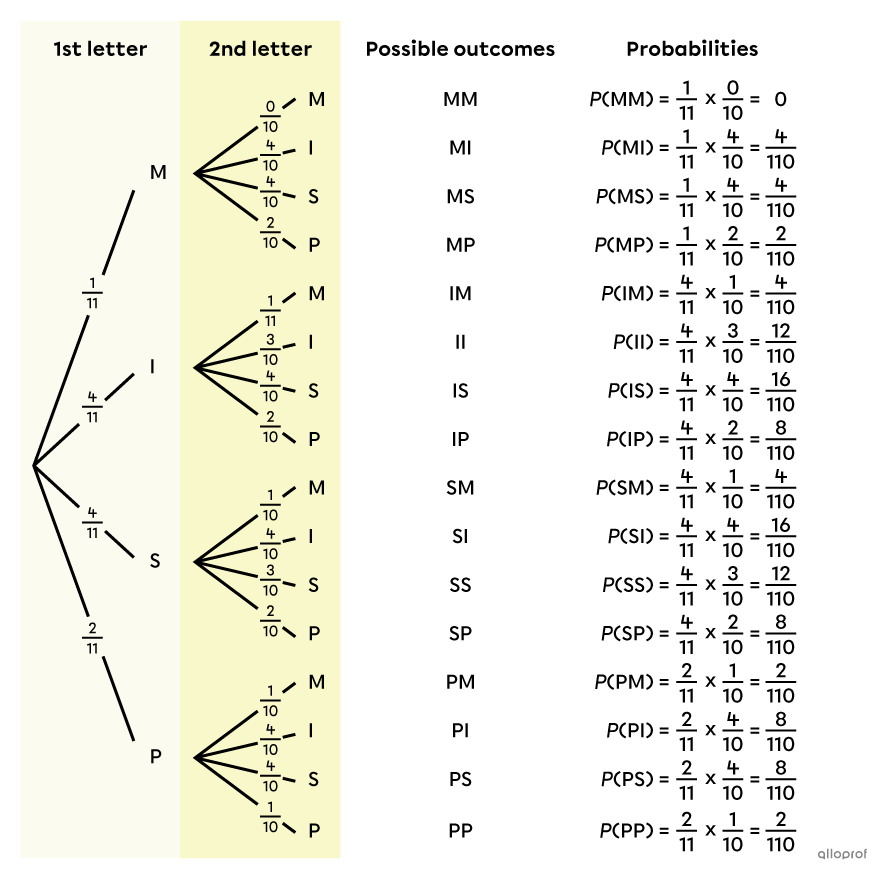
Note: On the probability tree, the fractions could have been reduced, but since there are fractions that must be added to complete the problem, it is easier not to simplify them yet.
-
Calculate the probability sought.
Remember that Romy wants to know the probability of her code being composed of 2 different letters. This can be done by adding up the probability of all the favourable outcomes: MI, MS, MP, IM, IS, IP, SM, SI, SP, PM, PI and PS.
We can also calculate |100\ \%| minus the probability of getting two identical letters. This way, fewer calculations are required.
||\begin{align}P(\text{getting 2 different letters})&=100\ \% -\big(P(\text{MM})+P(\text{II})+P(\text{SS}) + P(\text{PP})\big)\\&=\dfrac{110}{110}-\left(\dfrac{0}{110}+\dfrac{12}{110}+\dfrac{12}{110}+\dfrac{2}{110}\right)\\&=\dfrac{110}{110}-\dfrac{26}{110}\\&=\dfrac{84}{110}\end{align}||
Answer: The probability that Romy's code is composed of 2 different letters is |\dfrac{84}{110},| or about |76\ \%.|
The last 2 examples are problems of arrangements with and without replacement.
Tree diagrams are also found in other branches of mathematics.
-
In arithmetic, a factor tree is used to find the prime factorization of a number.
-
In graph theory, a tree is a connected graph that has no simple cycle.