When solving an optimization problem, look for a solution that maximizes or minimizes the function to be optimized, which is defined according to an objective. This is done by respecting constraints that are represented by a system of inequalities. On the Cartesian plane, these inequalities form a polygon of constraints and one or more vertices of this polygon corresponds to the solution sought.
-
Identify the variables.
To determine the variables, we look for elements which may vary, and not the element being optimized. Problems that are studied in high school only ever contain 2 variables.
-
Translate the constraints into a system of inequalities.
Each constraint is associated with a single inequality. In addition, if the variables represent quantities that cannot be negative, non-negative constraints must be set so there are only positive values. Here is a table containing some expressions that are regularly found in constraints, as well as the inequalities they represent.
|
Symbol |
Expressions |
|---|---|
|
|x<y| |
“|x| is less than |y|,” “|x| is smaller than |y|,” “|x| is (strictly) less than |y|,” etc. |
|
|x\leq y| |
“|x| is less than or equal to |y|,” “|x| is smaller than or equal to |y|,” “|x| is a maximum of |y|,” “|x| is at most equal to |y|,” “|x| is not more than |y|,” etc. |
|
|x>y| |
“|x| is greater than |y|,” “|x| is more than |y|,” “|x| exceeds |y|,” “|x| is (strictly) greater than |y|,” etc. |
|
|x\geq y| |
“|x| is greater than or equal to |y|,” “|x| is a minimum of |y|,” “|x| is at least equal to |y|,” “|x| is at least as much as |y|,” etc. |
-
Establish the rule of the function to be optimized |\boldsymbol{(z).}|
The rule of the function to be optimized can be written as |z=ax+by+c,| where |x| and |y| are the problem’s variables and |z| represents the quantity to be maximized or minimized. It is common for |z| to represent cost or revenue. In these cases, it is possible to use another variable, like |C| or |R.|
-
Graph the polygon of constraints.
To do so, graph all the inequalities on the Cartesian plane. The polygon of constraints is the common region on the Cartesian plane determined by the intersection of the solution sets of all the inequalities.
-
Determine the coordinates of the vertices of the polygon of constraints.
To find the coordinates of a vertex, take the equations of the 2 boundary lines that form the vertex and solve the system of equations. To do this, use the comparison method, the substitution method or the elimination method.
-
Find the optimal vertex (using a table or a scanning line).
Replace |x| and |y| in the function to be optimized with the coordinates of each point found in the previous step. Creating a table to compile all the outcomes is helpful. A scanning line can be used to reduce the number of vertices that need to be evaluated. The different |z| values must be then analyzed to determine the most advantageous one according to the objective.
-
Give a complete answer.
To answer the question, write a complete sentence containing the |(x,y)| pair that maximizes or minimizes the function, as well as the |z| value associated with this pair.
The scanning line technique is a way of reducing the number of vertices to evaluate when finding the optimal solution.
The scanning line is a line with a slope of |-\dfrac{a}{b}| that ‘scans’ the Cartesian plane, where |a| and |b| are the parameters of the function to be optimized |(z=ax+by+c).|
When the scanning line is slid along the Cartesian plane, the first and last vertices of the polygon of constraints it touches are the points that will either minimize or maximize the situation.
In the animation below, you can change parameters |a| and |b| of the function to be optimized using the sliders. You can also move the vertices of the polygon of constraints and slide the scanning line. To do so, simply move the green dot placed on the scanning line. When the scanning line is moved, its slope will always stay the same.
Pour valider ta compréhension à propos des problèmes d'optimisation de façon interactive, consulte la MiniRécup suivante.

Here is a complete example of an optimization problem. In this problem, the optimal solution is found using a table.
Melanie makes a living from her herd of |30| goats, each of which produces at most |20| litres of milk per week. She uses this milk to create |2| products that she sells at the market: yogurt and cream.
It takes |1.5\ \text{L}| of milk to make |1\ \text{L}| of yogurt. It also takes |6\ \text{L}| of milk to produce |1\ \text{L}| of cream.
Given the demand for her products, Melanie must produce at least |3| times more yogurt than cream and must produce at least |200\ \text{L}| of yogurt per week.
She sells her yogurt at the market for |\$36| per litre and her cream for |\$10| per litre.
How many litres of yogurt and litres of cream should Melanie produce per week to maximize her income?
-
Identify the variables.
|x:| number of litres of yogurt produced per week
|y:| number of litres of cream produced per week -
Translate the constraints into a system of inequalities.
|
Constraint |
Inequality |
|---|---|
|
It takes |1.5\ \text{L}| litres of milk to make |1\ \text{L}| of yogurt and |6\ \text{L}| of milk to make |1\ \text{L}| of cream. |
||1.5x + 6y \le 600|| |
|
The quantity of yogurt should be at least |3| times the quantity of cream. |
||x\ge 3y|| |
|
At least |200| litres of yogurt must be produced per week. |
||x\ge 200|| |
|
The number of litres of yogurt produced per week cannot be negative. |
||x\ge 0|| |
|
The number of litres of cream produced per week cannot be negative. |
||y\ge 0|| |
-
Establish the rule of the function to be optimized |\boldsymbol{(z)}.|
Melanie wants to maximize her income. She sells her yogurt for |\ $36\text{L}| and her cream for |\ $10\text{L}.| The function to be optimized is as follows:||R = 36x + 10y||where
|R:| revenue |(\$)| from the sale of yogurt and cream
-
Graph the polygon of constraints.
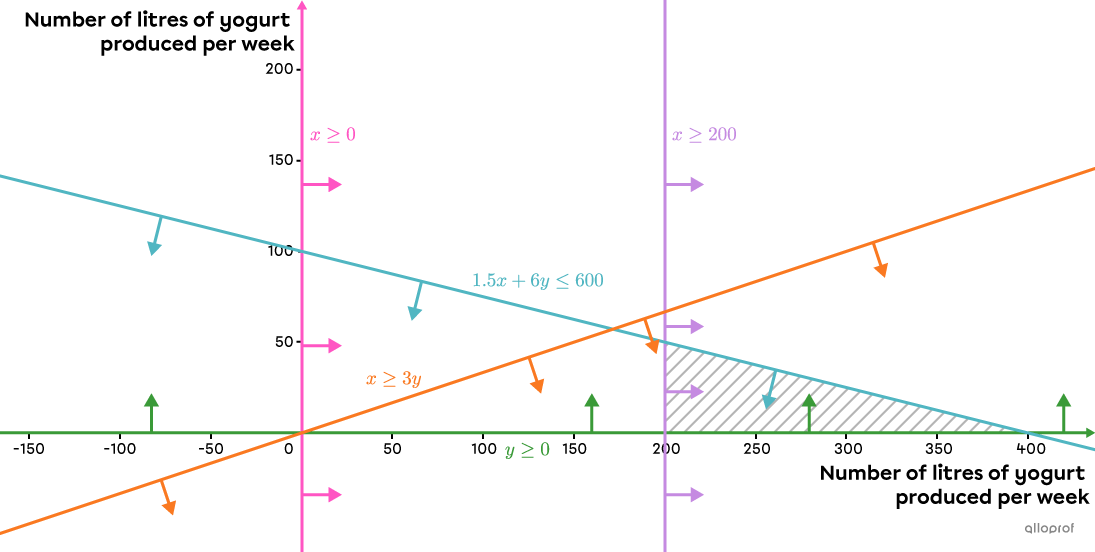
Note: The solution sets of the different inequalities are represented using arrows.
The polygon of constraints is a triangle, so there are 3 vertices. This implies that 2 of the inequalities are not directly used to form the polygon. Indeed, the inequality |x\ge0| is not needed, since the inequality |x\ge200| already implies that the |x| values are greater than |0.| As well, for |x| values greater than |200,| the solutions of the inequality |1.5x+6y\le600| automatically respect the inequality |x\ge3y.|
-
Determine the coordinates of the vertices of the polygon of constraints.
Using the methods for solving a system of linear equations, the coordinates of the vertices of the polygon of constraints can be found.
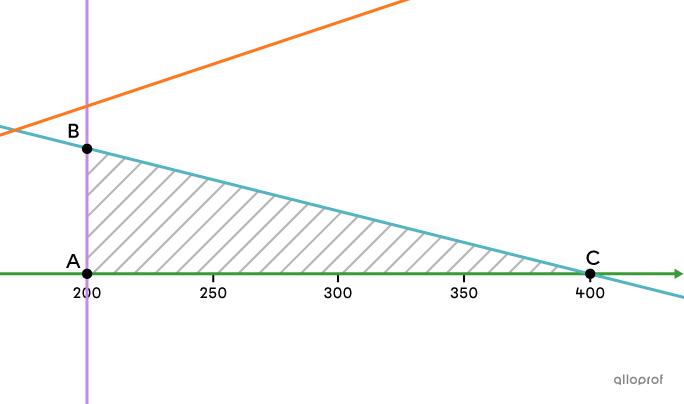
Vertex |\boldsymbol{A}| coordinates
The vertex is located at the intersection of lines |x=200| and |y=0.| Its coordinates are therefore the following:||A(200,0)||
Vertex |\boldsymbol{B}| coordinates
The vertex lies at the intersection of lines |1.5x+6y=600| and |x=200.| To find the coordinates, replace the |x| variable in the first equation with |200| and find the corresponding |y| value.||\begin{align}1.5x+6y&=600\\1.5(200)+6y&=600\\300+6y&=600\\6y&=300\\y&=50\end{align}||Its coordinates are therefore:||B(200,50)||
Vertex |\boldsymbol{C}| coordinates
The vertex is located at the intersection of lines |1.5x+6y=600| and |y=0.| To find its coordinates, replace the |y| variable in the first equation with |0| and find the corresponding |x| value.||\begin{align}1.5x+6y&=600\\1.5x+6(0)&=600\\1.5x&=600\\x&=400\end{align}||
Its coordinates are therefore:||C(400,0)||
-
Find the optimal vertex.
|
Vertex of the polygon |
Function to be optimized |
Income from the sale of yogurt and cream |
|---|---|---|
|
|A(200,0)| |
|\begin{align} R(x,y) &= 36x+10y \\ R(200,0) &= 36(200)+10(0) \\ &=7200 + 0 \\ &= \$7200\ \end{align}| |
|\$7200| |
|
|B(200,50)| |
|\begin{align} R(x,y) &= 36x+10y \\ R(200,50) &= 36(200)+10(50) \\ &=7200 + 500 \\ &= \$7700\ \end{align}| |
|\$7700 | |
|
|C(400,0)| |
|\begin{align} R(x,y) &= 36x+10y \\ R(400,0) &= 36(400)+10(0) \\ &=14\ 400 + 0 \\ &= \$14\ 400\ \end{align}| |
|\$14\ 400\ | |
Melanie wants to maximize her revenue. Since vertex |C| yields the maximum revenue, its coordinates optimize the situation.
-
Give a complete answer.
Melanie needs to produce |400\ \text{L}| of yogurt and not produce any cream to ensure the highest possible income of |\$14\ 400\ | per week.
Note: In this example, the scanning line technique can also be used to find the vertices that optimize the function. Then, the 2 vertices in question must be evaluated in the function to be optimized in order to find the vertex that maximizes the function.
In this 2nd example, a constraint was added. This means adding a new inequality that will change the polygon of constraints.
Victor sells skateboards. His professional skateboards cost |\ $300| and his standard skateboards cost |\ $50.| Due to his finances and the size of his store, he needs to respect certain constraints regarding the quantity of skateboards available in the store. The polygon below illustrates these constraints.
|x:| number of professional skateboards
|y:| number of standard skateboards

Victor wants to have a big sale next weekend. His sales consultant, John, suggests that he should have no more than |80| professional boards in stock at his store.
Should Victor follow John’s advice?
Since Victor wants to maximize his profits, the function to be maximized is as follows:||Z=300x+50y||
Calculate the profits from the initial polygon, using the function to be optimized, Z.
|
Vertex of the initial polygon |
Function to be optimized |
Profit |
|---|---|---|
|
|A(30,90)| |
|z=300(30)+50(90)| |
|\$13\ 500\ | |
|
|B(20,40)| |
|z=300(20)+50(40)| |
|\$8000\ | |
|
|C(50,10)| |
|z=300(50)+50(10)| |
|\$15\ 500\ | |
|
|D(110,50)| |
|z=300(110)+50(50)| |
|\$35\ 500\ | |
According to the initial polygon, the maximum possible profit is |\$35\ 500\ .|
By adding the new constraint recommended by John, the following polygon is created:
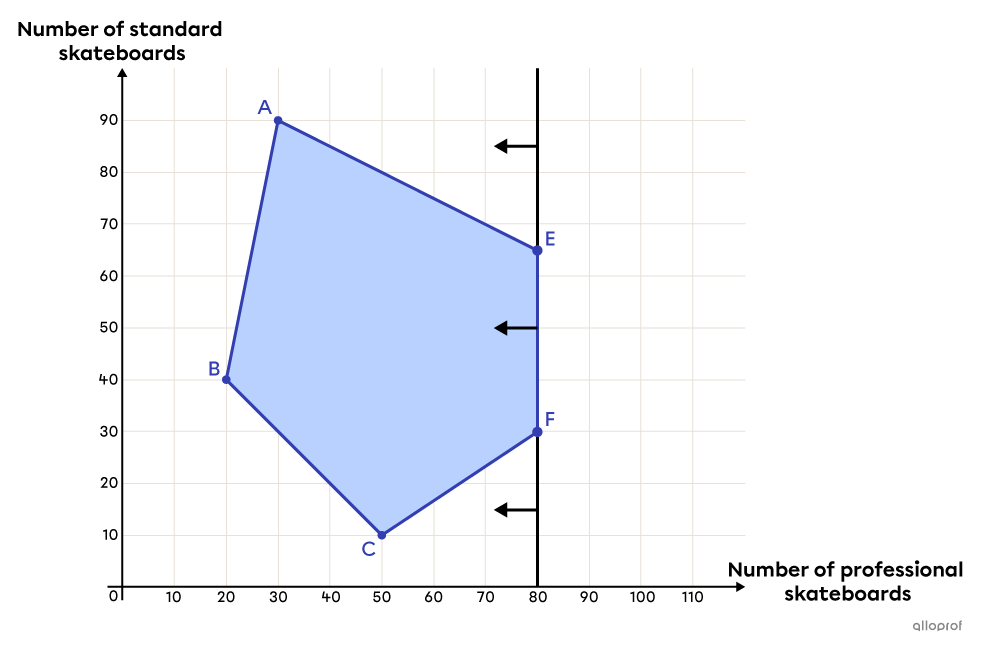
Calculate the profit associated with the polygon’s 2 new vertices.
|
Vertex of the polygon recommended by John |
Function to be optimized |
Profit |
|---|---|---|
|
|E(80,65)| |
|z=300(80)+50(65)| |
|\$27\ 250| |
|
|F(80,30)| |
|z=300(80)+50(30)| |
|\$25\ 500| |
Answer: With John’s recommendation, the maximum profit would be |\ $27\ 250.| So Victor should not follow John’s advice because he would lose out on |\ $8250\ | of profit.
When finding an optimal solution for a situation, it is possible to encounter some special cases.
When the constraints have strict inequality symbols |<| or |>,| the lines themselves are not included in the solution set. The graph will indicate this using a dotted line. If the vertex that optimizes the function is located on one or more dotted lines, the solution must be rejected since it does not respect all of the constraints. Test the points near and around this vertex that are part of the solution set and then choose the best one.
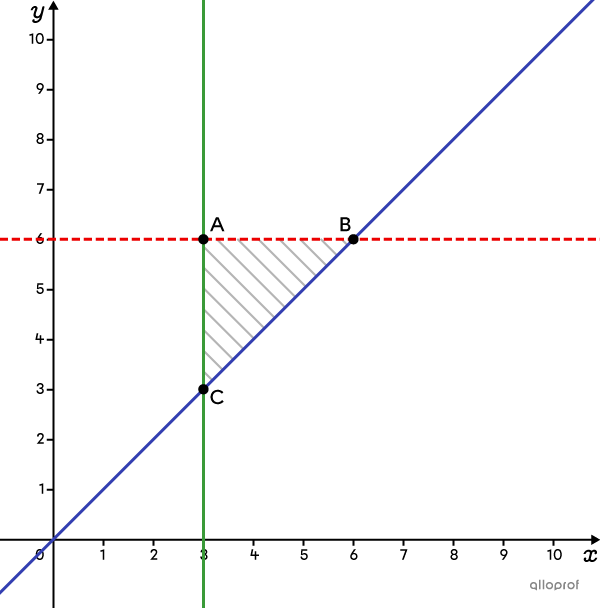
Depending on the context, sometimes the values of |x| and |y| must be integers. This is the case when |x| and |y| represent, for example, a number of objects, a number of animals or a number of people. However, the coordinates of the vertices of the polygon of constraints are not necessarily integers. When this happens, choose the point that has integer coordinates, that is part of the solution set, and that optimizes the situation.
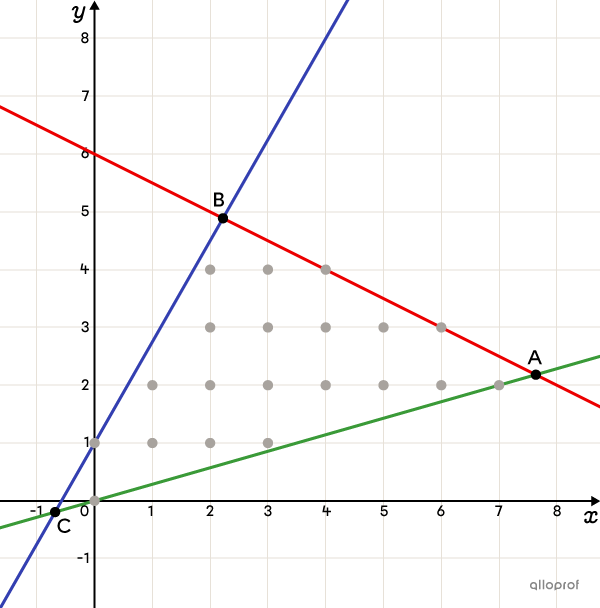
In the following example, vertex |A| and |B| do not have integer coordinates. If |A| is the vertex that optimizes the function |z,| then the point with integer coordinates that is the optimal solution and respects the context is either |(7,2)| or |(6,3).|
Sometimes, 2 vertices of the polygon optimize the function and give the same |z| value. When this is the case, it means that all the points located on the segment connecting these two vertices are optimal solutions. Therefore, there are several possible answers.
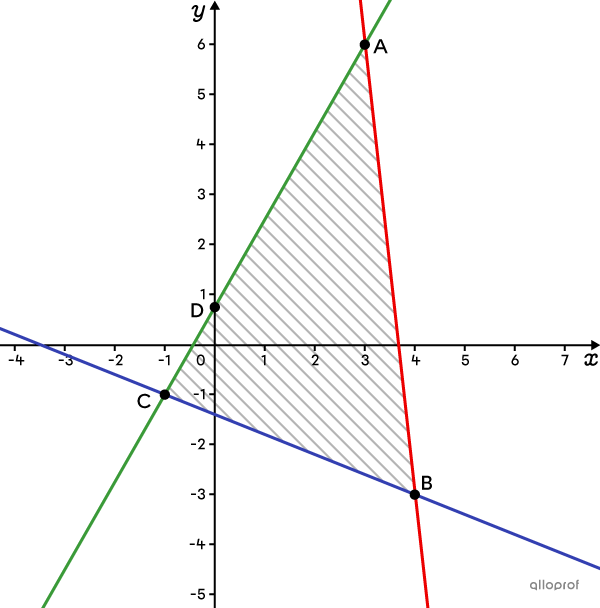
In the following example, vertices |A(3,6)| and |C(-1,-1)| both maximize the function with a |z| value of |3.| So, all the points on the segment |\overline{AC}| maximize it as well. Point |D(0,0.75)| is proof because it also yields a |z| of |3.|
|
Vertex of the polygon |
Function rule to be optimized |
Value of |\boldsymbol{z}| |
|---|---|---|
|
|A(3,6)| |
|z=-7(3)+4(6)| |
|3| |
|
|B(4,-3)| |
|z=-7(4)+4(-3)| |
|-40| |
|
|C(-1,-1)| |
|z=-7(-1)+4(-1)| |
|3| |
|
|D(0, 0.75)| |
|z=-7(0)+4(0.75)| |
|3| |
When a situation has several optimal solutions, the context sometimes provides an additional function to be optimized. This eliminates some of the solutions and makes it possible to find the one that optimizes both functions.
In the following example, there are 2 functions to be optimized. Start by finding the solutions that maximize the quantity of supplies to transport. Among these solutions, determine the one that minimizes the purchase cost.
Supplies are transported for disaster victims in 2 types of containers: bags and crates.
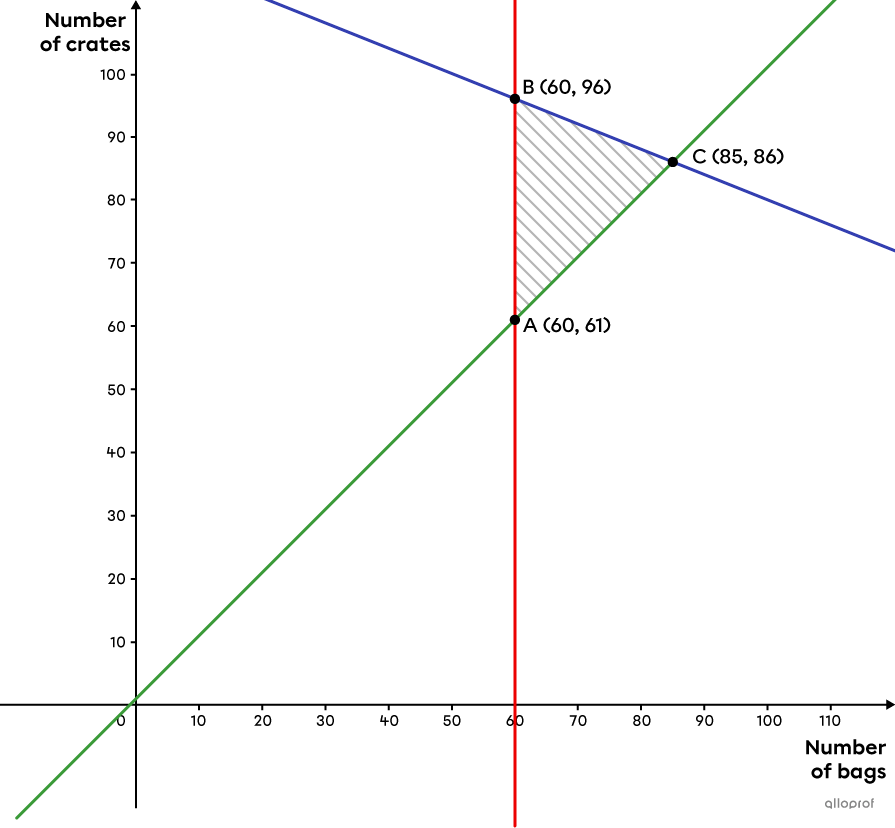
The polygon below represents the constraints associated with the number of bags and the number of crates that can be used.
Each bag can hold |10\ \text{kg}| of supplies and each crate can hold |25\ \text{kg}.| We want to maximize the quantity of supplies to deliver to the people affected by the disaster. In addition, bags can be purchased for |\$2\ | each and crates can be purchased for |\$8\ | each. The expenses associated with purchasing these containers must also be minimized.
The 1st function to be optimized involves the quantity of supplies to transport. The rule to be maximized is |Q=10x+25y.|
The 2nd function to be optimized involves the cost of the containers. The rule to be minimized is |C=2x+8y.|
Start by finding the one or more vertices that maximize the 1st function.
|
Vertex of the polygon |
Optimization rule |
Quantity of supplies |
|---|---|---|
|
|A(60,61)| |
|Q=10(60)+25(61)| |
|2125\ \text{kg}| |
|
|B(60,96)| |
|Q=10(60)+25(96)| |
|3000\ \text{kg}| |
|
|C(85,86)| |
|Q=10(85)+25(86)| |
|3000\ \text{kg}| |
Vertices |B| and |C| maximize the quantity of supplies to be delivered. This means all the points on the line segment connecting them are also solutions. However, since the number of bags and the number of crates must be integers, only the following points are valid solutions: |(60,96),| |(65,94),| |(70,92),| |(75,90),| |(80,88),| and |(85,86).| These points are found by testing all the integer values of |x| between |60| and |85| in the rule of the blue boundary line and choosing only those that result also in an integer value of |y|.
The 2nd function for minimizing the cost can now be used to analyze these points.
|
Point |
Optimization rule |
Cost |
|---|---|---|
|
|(60,96)| |
|C=2(60)+8(96)| |
|\$888| |
|
|(65,94)| |
|C=2(65)+8(94)| |
|\$882| |
|
|(70,92)| |
|C=2(70)+8(92)| |
|\$876| |
|
|(75,90)| |
|C=2(75)+8(90)| |
|\$870| |
|
|(80,88)| |
|C=2(80)+8(88)| |
|\$864| |
|
|(85,86)| |
|C=2(85)+8(86)| |
|\$858| |
So, with |85| bags and |86| crates, we maximize the quantity of supplies to be transported at |(3000\ \text{kg}),| while minimizing the cost of purchasing the containers at |(\$858).|