In a triangle, there are four types of lines with special properties that allow us to find the measure of specific angles or segments. These are called special lines.
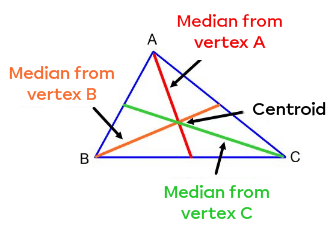
In a triangle, a median is a segment that connects a vertex to the midpoint of the opposite side.
Although this definition is given in terms of triangles, medians also exist in other plane figures.
The point where all 3 medians of any triangle intersect is called the centroid.
A median can also be constructed using geometric tools.
A perpendicular bisector is a line that passes through the midpoint of a segment and is perpendicular to that segment.
Perpendicular bisectors are usually found in plane figures but, unlike a median, are also found on line segments. Due to its position on a segment, it forms the line of symmetry of the segment it intersects.
The intersection point of the 3 perpendicular bisectors of any triangle is, in fact, the centre of the circle that circumscribes it.
To prove that this statement is always true for triangles, use the mouse to move each vertex wherever you like. You can also use the mouse to enlarge and slide the image so that the circle created can be clearly seen.
Like most line segments, it is always possible to construct a perpendicular bisector using geometric tools.
An angle bisector is a line or ray that divides an angle into 2 equal angles.
Once again, there is an interesting property relating to the angle bisectors that can be found by drawing them in any triangle. In short, the intersection point of the angle bisectors of a triangle corresponds to the centre of the inscribed circle of the triangle.
To prove that this statement is always true for any triangle, use the mouse to move each vertex wherever you like. You can also use the mouse to enlarge and slide the image so that the circle created can be clearly seen.
What’s more, we can construct an angle bisector using geometric tools.
The height (altitude) is a segment that connects a vertex to its opposite side or extended base and is perpendicular to this opposite side.
However, the height is not always a perfectly vertical segment. In fact, the focus is on the fact that it must be perpendicular to the opposite side onto which it is dropped.
Another interesting characteristic is that the point where the 3 heights intersect is the orthocentre of the triangle.
Depending on the type of triangle, this orthocentre may be situated outside the triangle.
Moreover, the height is not always inside the polygon.
Using geometric tools is the best way to accurately construct a height.
Move the vertices of the triangle to see the different properties of each special line.