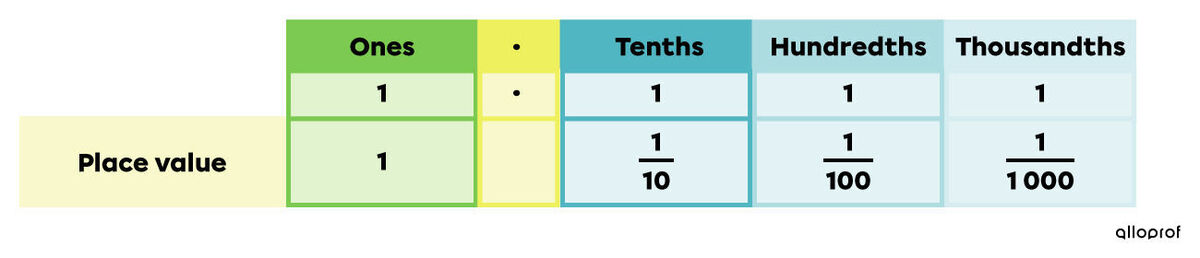
Decimal notation is a way of writing real numbers using an integer part and a decimal part separated by a decimal point.

When a number is written in decimal notation, each digit occupies a position linked to a specific value. This is called the place value.
The integer part refers to the digits to the left of the decimal point, namely the ones, tens, hundreds, etc. The decimal part includes the digits to the right of the decimal point, such as the tenths |\left(\dfrac{1}{10}\right)\!,| hundredths |\left(\dfrac{1}{100}\right)\!,| thousandths |\left(\dfrac{1}{1000}\right)\!,| etc.
Note: The decimal part of a number is sometimes called the fractional part, because it refers to a fraction of the whole.
When the decimal part of a number is repeated, that number is sometimes defined as a periodic number.
We call the repeating sequence a period.
Periodic numbers are also part of rational numbers.
To indicate a number’s decimal part is periodic, we draw a line above the repeating sequence (i.e., the period).
Here is an example of how to use decimal notation for each of the following categories of numbers.
Terminating Decimals ||1.4||
Repeating Decimals ||2.\overline{5}||
Irrational Numbers ||\pi=3.141592654…||
A terminating decimal number is a rational number whose decimal part has a finite number of digits.

If a given fraction of integers is equivalent to a fraction whose denominator is a power of |10,| then that fraction is a terminating decimal number; otherwise, it is a repeating decimal number.
Fractions whose denominator is a power of |10| are called decimal fractions.
Terminating Decimals
-
|\dfrac{1}{\bf{2}}\begin{align}\times\,\color{#3a9a38}{\bf{5}}\\[-1pt] \times\,\color{#3a9a38}{\bf{5}}\end{align}= \dfrac{5}{10}=0.5|
-
|\dfrac{3}{\bf{5}}\begin{align}\times\,\color{#3a9a38}{\bf{2}}\\[-1pt] \times\,\color{#3a9a38}{\bf{2}}\end{align}= \dfrac{6}{10}=0.6|
-
|\dfrac{14}{20}\begin{align}\div\,\color{#3a9a38}{\bf{2}}\\[-1pt] \div\,\color{#3a9a38}{\bf{2}}\end{align}= \dfrac{7}{10}=0.7|
-
|\dfrac{3}{4}\begin{align}\times\,\color{#3a9a38}{\bf{25}}\\[-1pt] \times\,\color{#3a9a38}{\bf{25}}\end{align}= \dfrac{75}{100}=0.75|
-
|\dfrac{12}{25}\begin{align}\times\,\color{#3a9a38}{\bf{4}}\\[-1pt] \times\,\color{#3a9a38}{\bf{4}}\end{align}= \dfrac{48}{100}=0.48|
-
|\dfrac{7}{8}\begin{align}\times\,\color{#3a9a38}{\bf{125}}\\[-1pt] \times\,\color{#3a9a38}{\bf{125}}\end{align}= \dfrac{875}{1000}=0.875|
-
|\dfrac{3}{6}\begin{aligned}\div\,\color{#3a9a38}{\bf{3}}\\[-1pt] \div\,\color{#3a9a38}{\bf{3}}\end{aligned}= \dfrac{1}{\bf{2}}\begin{aligned}\times\,\color{#3a9a38}{\bf{5}}\\[-1pt] \times\,\color{#3a9a38}{\bf{5}}\end{aligned}= \dfrac{5}{10}=0.5|
Repeating Decimals
-
|\dfrac{1}{\bf{3}}\begin{align}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{align}=\, \dfrac{\color{#ec0000}{\bf{?}}}{10...}|
There is no integer that can be used to convert |\dfrac{1}{3}| into a fraction with |10| as a denominator or any other power of |10.| Therefore, |\dfrac{1}{3}| does not represent a terminating decimal, but a repeating decimal.
|\dfrac{1}{3} =0.333333...=0.\overline{3}|
-
|\begin{align}\dfrac{2}{\bf{7}}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}&=\ \dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{2}{7} &=0.285714285...=0{,}\overline{285714} \end{align}|
-
|\begin{align}\dfrac{4}{9}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}&=\ \dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{4}{9} &=0.444...=0.\overline{4} \end{align}|
-
|\begin{align}\dfrac{4}{6}\begin{aligned}\,\div\ \,\color{#3a9a38}{\bf{2}}\\[-1pt] \div\ \,\color{#3a9a38}{\bf{2}}\end{aligned}&=\ \dfrac{2}{\bf{3}}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}\, =\,\dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{4}{6}=\dfrac{2}{3}&=0.666...=0.\overline{6}\end{align}|
A repeating decimal, also called a periodic number, is a rational number whose decimal part consists of a sequence of digits that repeats itself.
The part that repeats itself is called the period.
To indicate that a number’s decimal part is periodic, we draw a line above the repeating part (i.e., the period).
|\dfrac{4}{3}=1.333333...=1.\overline{3}|
The period is |3.|
|\dfrac{35}{11}=3.181818181...=3.\overline{18}|
The period is |18.|
It is not always the entire decimal part of a number that repeats itself.
|\dfrac{38}{15}=2.533333...=2.5\overline{3}|
The period is only |3.| The digit |5| does not repeat.
|\dfrac{41}{12}=3.416666666...=3.41\overline{6}|
The period is only |6.| The digits |4| and |1| do not repeat.
Calculators can sometimes be misleading. Many models round off the last displayed digit in the decimal part, which can lead us to believe that the number is not periodic, when in fact it is.
For example, to find the decimal notation of the fraction |\dfrac{2}{3},| you need to divide |2| by |3.| Most calculators display |0.666666667.| All rational numbers (i.e. those that can be written as a fraction of integers) are repeating numbers.||\dfrac{2}{3}=0.666666…=0.\overline{6}||

An irrational number is a number whose decimal part is non-terminating and non-repeating.
|\sqrt{2},| written in decimal notation is: |1.414213562…|
Although it is possible to write an approximation of the number |\sqrt{2}| using decimal notation, it is not a terminating decimal since the decimal part does not have a finite number of digits. It is also not a repeating decimal since it does not have a sequence of digits that repeats indefinitely. |\sqrt{2}| is therefore an irrational number.
Here are some other examples of irrational numbers with their representation in decimal notation.
|\begin{align}\dfrac{\sqrt{5}}{2}&=1.118033989…\\[4pt] \pi&=3.141592654…\end{align}|
The golden ratio: |\varphi=1.618033989…|
Radicals are not necessarily irrational numbers. They can be integers or terminating decimals.
-
|\sqrt{9}=3| is an integer.
-
|\sqrt{12.96}=3.6| is a terminating decimal.