A trigonometric angle is a central angle in the unit circle that results from a rotation starting from the positive part of the |x| axis.
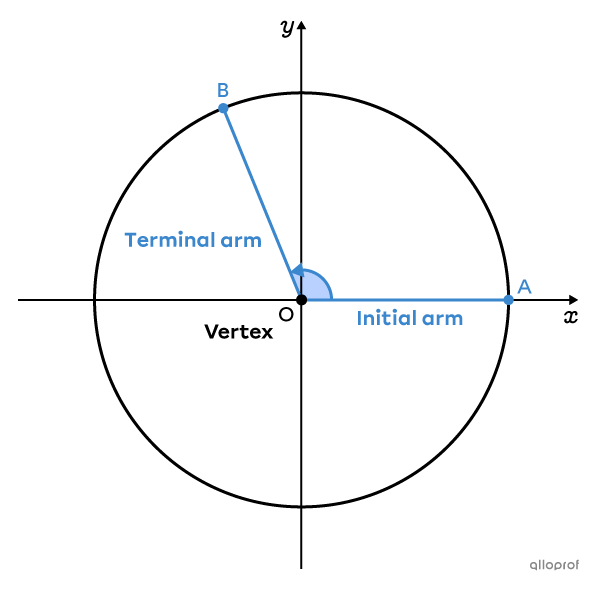
There are 3 elements of a trigonometric angle:
-
the vertex |(O),| located at the centre of the circle;
-
the initial arm |(\overline{AO}),| which is the side of the angle that coincides with the positive |x|-axis;
-
the terminal arm |(\overline{BO}),| which is the side of the angle obtained after rotating the initial arm around the centre of the circle.
Note: Both the initial and terminal arm of the angle are radii of the unit circle.
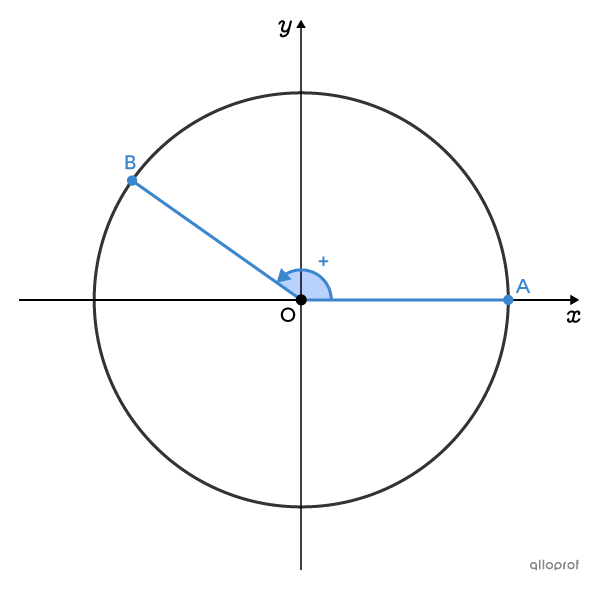
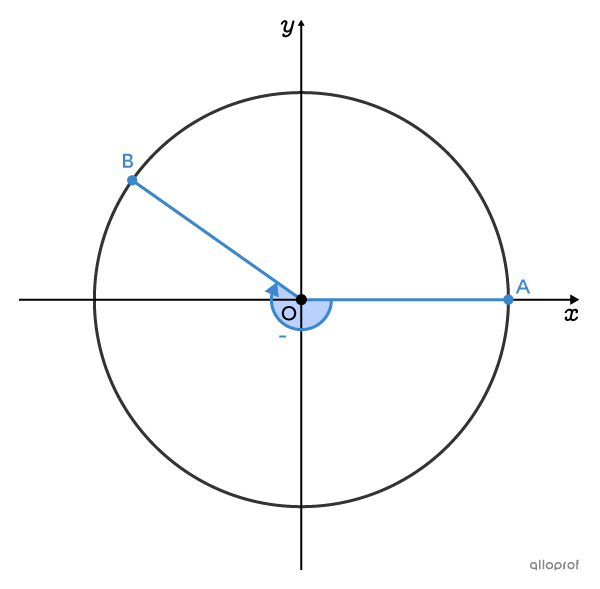
There are 2 different ways to analyze the same angle: using a counterclockwise rotation or a clockwise rotation. This affects the sign of the angle value.
If the initial arm rotates counterclockwise, the angle measure is positive.
If the initial arm rotates clockwise, the angle measure is negative.
When working with the unit circle, radians are used, not degrees.
One radian |(1\ \text{rad})| corresponds to the measure of the central angle whose sides intercept a circle arc whose length is equal to the radius of the circle.
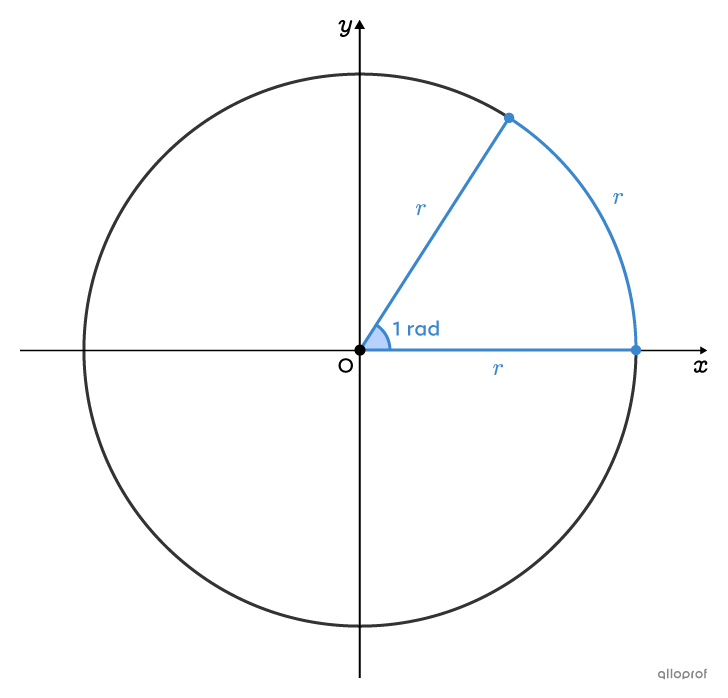
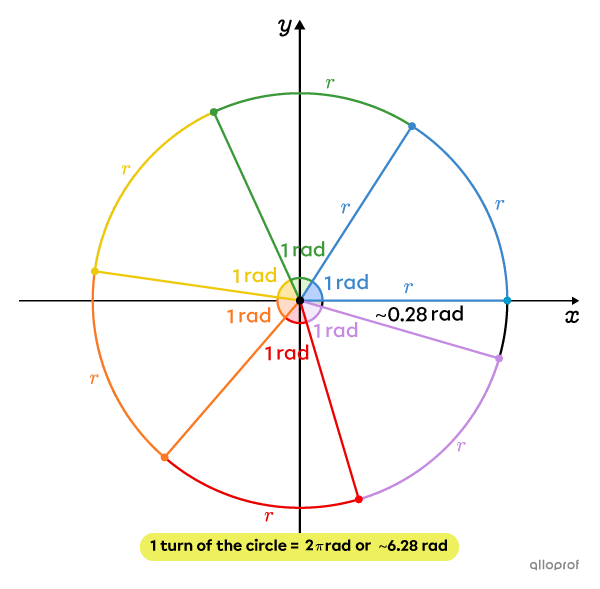
To find the angle formed by one complete rotation in radians, the following equation is solved:||\begin{align}\dfrac{1\ \text{rad}}{?\ \text{rad}}&=\dfrac{\text{Arc length equivalent to}\ 1\ \text{radius}}{\text{Circumference of the circle}}\\\\\dfrac{1}{?}&=\dfrac{r}{2\pi r}\\\\?&=\dfrac{1 \times 2\pi r}{r}\\\\?&=2\pi\ \text{rad}\end{align}||Therefore, the angle formed by one complete turn is equal to |2\pi\ \text{rad}\approx6.28\ \text{rad}.|
The image illustrates that |6\ \text{rad}| fit completely into the circle, along with a smaller part, which represents about |0.28\ \text{rad}.|
The equivalence in radians of some of the main angles can be determined from the fact that |360^\circ=2\pi\ \text{rad},|.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{2}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{2}}\\\\180^\circ&=\pi\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{4}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{4}}\\\\90^\circ&=\dfrac{\pi}{2}\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{6}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{6}}\\\\60^\circ&=\dfrac{\pi}{3}\ \text{rad}\end{align}||
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{360^\circ}}{12}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi\ \text{rad}}}{12}}\\\\30^\circ&=\dfrac{\pi}{6}\ \text{rad}\end{align}||
Using this method, we can determine the radian equivalence of several angles.
|
Angle in degrees |\boldsymbol{(^\circ)}| |
|30| |
|45| |
|60| |
|90| |
|120| |
|135| |
|150| |
|180| |
|210| |
|225| |
|240| |
|270| |
|300| |
|315| |
|330| |
|360| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Angle in radians |\boldsymbol{(\text{rad})}| |
|\dfrac{\pi}{6}| |
|\dfrac{\pi}{4}| |
|\dfrac{\pi}{3}| |
|\dfrac{\pi}{2}| |
|\dfrac{2\pi}{3}| |
|\dfrac{3\pi}{4}| |
|\dfrac{5\pi}{6}| |
|\pi| |
|\dfrac{7\pi}{6}| |
|\dfrac{5\pi}{4}| |
|\dfrac{4\pi}{3}| |
|\dfrac{3\pi}{2}| |
|\dfrac{5\pi}{3}| |
|\dfrac{7\pi}{4}| |
|\dfrac{11\pi}{6}| |
|2\pi| |
To switch from one unit of measure to another, a proportion must be established. This is possible based on the fact that one full circular rotation is equivalent to |2\pi\ \text{rad}| and |360^\circ.|
||\dfrac{\text{Central angle in degrees}}{360^\circ}=\dfrac{\text{Central angle in radians}}{2\pi\ \text{rad}}||
Find the measure of a |\dfrac{7\pi}{12}\ \text{rad}| angle in degrees.||\begin{align}\dfrac{\theta}{360^\circ}&=\dfrac{\color{#3a9a38}{\frac{7\pi}{12}\ \text{rad}}}{2\pi\ \text{rad}}\\\\
\theta&=\dfrac{360\times \frac{7\pi}{12}}{2\pi}\\ \theta&=105^\circ\end{align}||Answer: The angle measures |105^\circ.|
Find the measure of a |144^\circ| angle in radians.||\begin{align}\dfrac{\color{#3a9a38}{144^\circ}}{360^\circ}&=\dfrac{\theta}{2\pi\ \text{rad}}\\\\ \theta&=\dfrac{144 \times 2\pi}{360}\\\theta&=\dfrac{2\pi}{5}\ \text{rad}\end{align}||Answer: The angle measures |\dfrac{2\pi}{5}\ \text{rad}.|
To determine the measure of an arc, the following proportion can be established. ||\begin{align}\dfrac{\text{Central angle in degrees}}{360^\circ}&=\dfrac{\text{Intercepted arc}}{\text{Circumference of the circle}}\\\\
\dfrac{\theta}{360^\circ}&=\dfrac{L}{2\pi r}\end{align}||Since |360^\circ| is equivalent to |2\pi| radians, the following proportion exists, which is then simplified.||\begin{align}\dfrac{\theta\ \text{rad}}{\cancel{2\pi}\ \text{rad}}&=\dfrac{L}{\cancel{2\pi} r}\\\\
\dfrac{\theta\ \text{rad}}{1\ \text{rad}}&=\dfrac{L}{r}\end{align}||Manipulating the above proportion yields the following formula.
|L=\theta \times r|
where
|L|: arc length
|\theta|: central angle in radians
|r|: radius

This means the sides of a central angle of |\theta\ \text{rad}| intercept an arc whose length |(L)| is equal to |\theta| multiplied by the radius |r.|
Using the formula |L=\theta \times r| find the radius of a circle whose central angle is |220^\circ| when its intercepted arc length is |15\ \text{cm}.|
Start by converting |220^\circ| into radians.||\begin{align}\dfrac{\color{#3a9a38}{220^\circ}}{360^\circ}&=\dfrac{\theta}{2\pi\ \text{rad}}\\\\\dfrac{220\times 2\pi}{360}&=\theta\\\\\dfrac{11\pi}{9}\ \text{rad}&=\theta\end{align}||Now find the radius.||\begin{align}L&=\theta\times r\\15&=\dfrac{11\pi}{9}\times r\\15\times{\frac{9}{11\pi}}&=r\\3.91\ \text{cm}&\approx r\end{align}||Answer: The radius is about |3.91\ \text{cm}.|