A trigonometric identity is an equation that is always true, derived from the relationships between various trigonometric ratios.
The right triangle can be used to define various trigonometric ratios, which can then be transposed onto the unit circle.
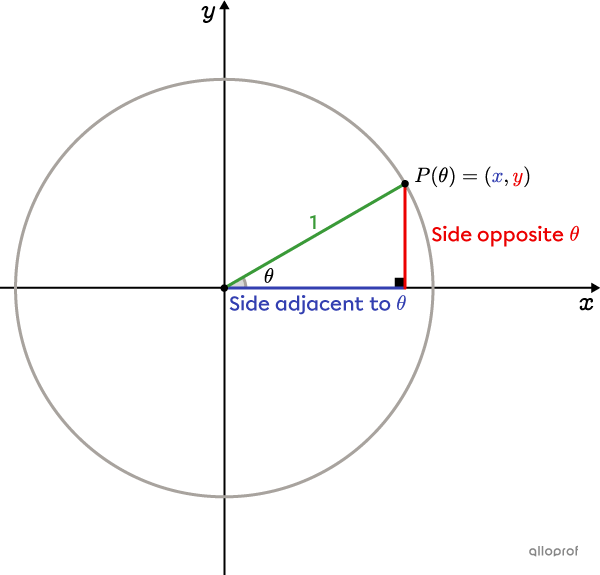
The sine ratio
||\sin\theta=\dfrac{\color{#ec0000}y}{\color{#3a9a38}1}=y||The sine of an angle |\theta| corresponds to the |y|-coordinate of the trigonometric point |P(\theta).|
The cosine ratio
||\cos\theta=\dfrac{\color{#333fb1}x}{\color{#3a9a38}1}=x||The cosine of an angle |\theta| corresponds to the |x|-coordinate of the trigonometric point |P(\theta).|
The tangent ratio
||\tan\theta=\dfrac{\sin\theta}{\cos\theta}=\dfrac{\color{#ec0000}y}{\color{#333fb1}x}||The tangent of an angle |\theta| corresponds to the ratio between the y-coordinate |(y)| and the x-coordinate |(x)| of the trigonometric point |P(\theta).|
The next 3 ratios are the reciprocal of the 3 previous ratios.
The cosecant ratio
The cosecant ratio of an angle |\theta| is the reciprocal of the sine of the angle |\theta.|||\text{csc}\ \theta=\dfrac{1}{\sin\theta}||
The secant ratio
The secant ratio of an angle |\theta| is the reciprocal of the cosine of the angle |\theta.|||\text{sec}\ \theta=\dfrac{1}{\cos\theta}||
The cotangent ratio
The cotangent ratio of an angle |\theta| is the reciprocal of the tangent of the angle |\theta.|||\text{cot}\ \theta=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta}||
Note: Both |\csc| or |\text{cosec}| can be used as the notation for cosecant and |\cot| or |\text{cotan}| can both be used as the notation for cotangent.
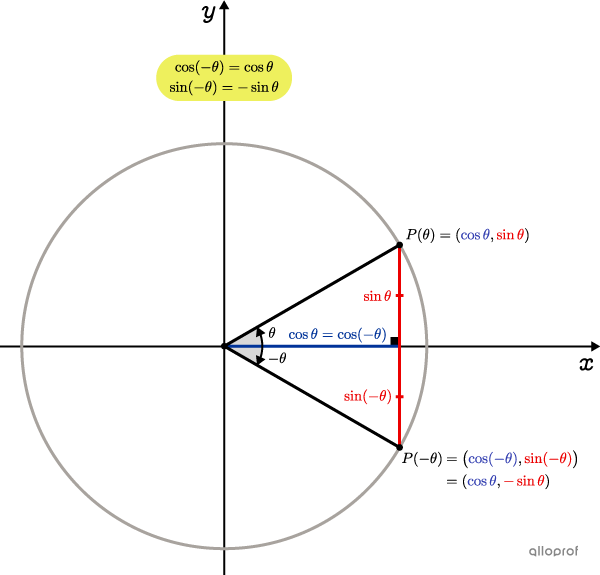
The |x|-coordinate of point |P(-\theta)| is the same as the |x|-coordinate of point |P(\theta).| The |y|-coordinate of |P(-\theta)| is the opposite of the |y|-coordinate of |P(\theta).|
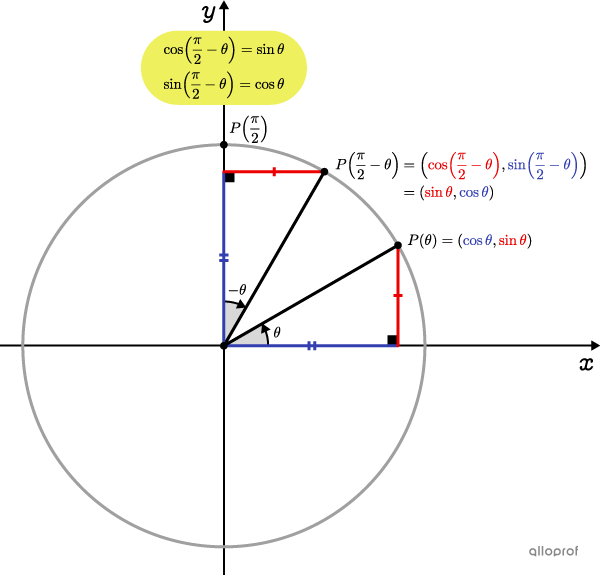
The |x|-coordinate of point |P\left(\dfrac{\pi}{2}-\theta\right)| is the |y|-coordinate of point |P(\theta).| Similarly, the |y|-coordinate of |P\left(\dfrac{\pi}{2}-\theta\right)| is the |x|-coordinate of |P(\theta).|
Here is how to determine the value of a trigonometric expression using only the definition of the ratios.
-
Determine the coordinates of trigonometric point |P(\theta).|
-
Rewrite the expression in terms of |\sin\theta| and/or |\cos\theta.|
-
Replace the coordinates in the expression.
-
Determine the value of the expression.
Determine the exact value of the trigonometric expression |\tan\left(\dfrac{2\pi}{3}\right).|
-
Determine the coordinates of the trigonometric point |\boldsymbol{P(\theta)}.|
||P\left(\dfrac{2\pi}{3}\right)=\left(\color{#333fb1}{-\dfrac{1}{2}},\color{#ec0000}{\dfrac{\sqrt{3}}{2}}\right)|| -
Rewrite the expression in terms of |\boldsymbol{\sin\theta}| and/or |\boldsymbol{\cos\theta}.|
||\tan\left(\dfrac{2\pi}{3}\right)=\dfrac{\sin\left(\dfrac{2\pi}{3}\right)}{\cos\left(\dfrac{2\pi}{3}\right)}|| -
Replace the coordinates in the expression.
||\tan\left(\dfrac{2\pi}{3}\right)=\dfrac{\color{#ec0000}{\dfrac{\sqrt{3}}{2}}}{\color{#333fb1}{-\dfrac{1}{2}}}|| -
Determine the value of the expression.
||\begin{align}\tan\left(\dfrac{2\pi}{3}\right)&=\dfrac{\sqrt{3}}{2}\times-\dfrac{2}{1}\\&=-\dfrac{2\sqrt{3}}{2}\\&=-\sqrt{3}\end{align}||
Answer: The exact value of |\tan\left(\dfrac{2\pi}{3}\right)| is |-\sqrt{3}.|
Determine the exact value of the expression |\sec\left(\dfrac{5\pi}{4}\right).|
-
Determine the coordinates of the trigonometric point |\boldsymbol{P(\theta)}.|
||P\left(\dfrac{5\pi}{4}\right)=\left(\color{#333fb1}{-\dfrac{\sqrt{2}}{2}},\color{#ec0000}{-\dfrac{\sqrt{2}}{2}}\right)|| -
Rewrite the expression in terms of |\boldsymbol{\sin\theta}| and/or |\boldsymbol{\cos\theta}.|
||\sec\left(\dfrac{5\pi}{4}\right)=\dfrac{1}{\cos\left(\dfrac{5\pi}{4}\right)}|| -
Replace the coordinates in the expression.
||\sec\left(\dfrac{5\pi}{4}\right)=\dfrac{1}{\color{#333fb1}{-\dfrac{\sqrt{2}}{2}}}|| -
Determine the value of the expression.
||\begin{align}\sec\left(\dfrac{5\pi}{4}\right)&=1\times-\dfrac{2}{\sqrt{2}}\\&=-\dfrac{2}{\sqrt{2}}\end{align}||The fraction must be rationalized to remove the radical from the denominator.||\begin{align}\sec\left(\dfrac{5\pi}{4}\right)&=-\dfrac{2}{\sqrt{2}}\color{#ec0000}{\times\dfrac{\sqrt{2}}{\sqrt{2}}}\\&=-\dfrac{2\sqrt{2}}{2}\\&=-\sqrt{2}\end{align}||
Answer: The exact value of |\sec\left(\dfrac{5\pi}{4}\right)| is |-\sqrt{2}.|
It is possible for an angle to be greater than |2 \pi\ \text{rad}| |(360^\circ),| which indicates more than one rotation around the unit circle. To find what angle it corresponds to within the |[0,2\pi]| interval, subtract a certain number of |2\pi| rotations to find the equivalent point on the circle.
Below are the steps for evaluating a trigonometric expression with an angle that is not in the interval |[0,2\pi].|
-
Calculate the number of rotations to subtract from the angle |\theta| by dividing this angle measure by |2\pi| and retaining the integer part of the answer.||N=\left[\dfrac{\theta}{2\pi}\right]||
-
Subtract the angle created by the number of rotations calculated |(N)| from the angle |\theta.|||\theta\, '=\theta-(N\times 2\pi)||
-
Position the outcome (the angle between |0| and |2\pi|) on the unit circle and find its |x| and |y| coordinates.
-
Determine the value of the given trigonometric expression using its coordinates.
Determine the exact value of |\csc\left(\dfrac{47\pi}{6}\right).|
-
Calculate the number of rotations.
||\begin{align}N&=\left[\dfrac{\theta}{2\pi}\right]\\&=\left[\dfrac{\frac{47\pi}{6}}{2\pi}\right]\\&=\left[\dfrac{47\pi}{6}\times\dfrac{1}{2\pi}\right]\\&=\left[\dfrac{47}{12}\right]\\&=\left[3.91\overline{6}\right]\\&=3\end{align}|| -
Subtract the angle created by the rotations.
||\begin{align}\theta\, '&=\color{#3a9a38}\theta-(\color{#3a9a38}N\times2\pi)\\&=\color{#3a9a38}{\dfrac{47\pi}{6}}-(\color{#3a9a38}3\times2\pi)\\&=\dfrac{47\pi}{6}-6\pi\\&=\dfrac{47\pi}{6}-\dfrac{36\pi}{6}\\&=\dfrac{11\pi}{6}\end{align}|| -
Find the coordinates.
Point |P\left(\dfrac{47\pi}{6}\right)| coincides with point |P\left(\dfrac{11\pi}{6}\right).| Its coordinates are as follows:||P\left(\dfrac{47\pi}{6}\right)=P\left(\dfrac{11\pi}{6}\right)=\left(\color{#333fb1}{\dfrac{\sqrt{3}}{2}},\color{#ec0000}{-\dfrac{1}{2}}\right)|| -
Determine the value of the expression.
||\begin{align}\text{csc}\left(\dfrac{47\pi}{6}\right)&=\dfrac{1}{\color{#ec0000}{\sin\left(\dfrac{47\pi}{6}\right)}}\\&=\dfrac{1}{\color{#ec0000}{-\dfrac{1}{2}}}\\&=1\times-\dfrac{2}{1}\\&=-2\end{align}||
Answer: The exact value of |\text{csc}\left(\dfrac{47\pi}{6}\right)| is |-2.|
Calculate the exact value of |\cot\left(-\dfrac{79\pi}{3}\right).|
-
Calculate the number of rotations.
||\begin{align}N&=\left[\dfrac{\theta}{2\pi}\right]\\&=\left[\dfrac{-\frac{79\pi}{3}}{2\pi}\right]\\&=\left[-\dfrac{79\pi}{3}\times\dfrac{1}{2\pi}\right]\\&=\left[-\dfrac{79}{6}\right]\\&=\left[-13.1\overline{6}\right]\\&=-14\end{align}||Here, we must determine the greatest integer part of a negative number. This results in a negative number of revolutions. This means that the angle of rotation for determining the number of revolutions is in the clockwise direction. -
Subtract the angle created by the rotations.
||\begin{align}\theta\ '&=\color{#3a9a38}\theta-(\color{#3a9a38}N\times2\pi)\\&=\color{#3a9a38}{-\dfrac{79\pi}{3}}-(\color{#3a9a38}{-14}\times2\pi)\\&=-\dfrac{79\pi}{3}+28\pi\\&=-\dfrac{79\pi}{3}+\dfrac{84\pi}{3}\\&=\dfrac{5\pi}{3}\end{align}|| -
Find the coordinates.
Point |P\left(-\dfrac{79\pi}{3}\right)| coincides with point |P\left(\dfrac{5\pi}{3}\right).| So, its coordinates are as follows:
||P\left(-\dfrac{79\pi}{3}\right)=P\left(\dfrac{5\pi}{3}\right)=\left(\color{#333fb1}{\dfrac{1}{2}},\color{#ec0000}{-\dfrac{\sqrt{3}}{2}}\right)|| -
Determine the value of the expression.
||\begin{align}\text{cot}\left(-\dfrac{79\pi}{3}\right)&=\text{cotan}\left(\dfrac{5\pi}{3}\right)\\&=\dfrac{\color{#333fb1}{\cos\left(\dfrac{5\pi}{3}\right)}}{\color{#ec0000}{\sin\left(\dfrac{5\pi}{3}\right)}}\\&=\dfrac{\color{#333fb1}{\dfrac{1}{2}}}{\color{#ec0000}{-\dfrac{\sqrt{3}}{2}}}\\&=\dfrac{1}{2}\times-\dfrac{2}{\sqrt{3}}\\&=-\dfrac{1}{\sqrt{3}}\\&=-\dfrac{1}{\sqrt{3}}\times\dfrac{\sqrt{3}}{\sqrt{3}}\\&=-\dfrac{\sqrt{3}}{3}\end{align}||
Answer: The exact value of |\text{cot}\left(-\dfrac{79\pi}{3}\right)| is |-\dfrac{\sqrt{3}}{3}.|
Pythagorean trigonometric identities are helpful when proving trigonometric identities.
||\begin{alignat}{13}\cos^2\theta\ \,&+\,\sin^2\theta&&=\quad\ 1\\1\quad\ \,&+\tan^2\theta&&=\ \sec^2\theta\\\text{cotan}^2\theta&+\quad1&&=\text{cosec}^2\theta\end{alignat}||
Here are the proofs of the 3 Pythagorean identities.
From the unit circle and the Pythagorean theorem, the 1st Pythagorean identity can be derived.||\begin{align}\color{#333fb1}a^2 + \color{#ec0000}b^2 &=\color{#3a9a38}c^2\\ \color{#333fb1}{(\cos\theta)}^2 + \color{#ec0000}{(\sin\theta)}^2 &=\color{#3a9a38}{(1)}^2\\ \cos^2 \theta + \sin^2 \theta &=1 \end{align}||Dividing all the terms of this previous equation by |\cos^2 \theta| gives the 2nd identity.||\begin{align}\dfrac{\cos^2 \theta}{\cos^2 \theta} + \dfrac{\sin^2 \theta}{\cos^2 \theta} &= \dfrac{1}{\cos^2\theta}\\\\1 + \tan^2 \theta &= \sec^2 \theta\end{align}||Dividing all the terms of the 1st identity by |\sin^2 \theta| gives the 3rd identity.||\begin{align}\dfrac{\cos^2 \theta}{\sin^2 \theta} + \dfrac{\sin^2 \theta}{\sin^2 \theta} &= \dfrac{1}{\sin^2\theta}\\\\\cot^2 \theta + 1 &= \text{csc}^2 \theta\end{align}||
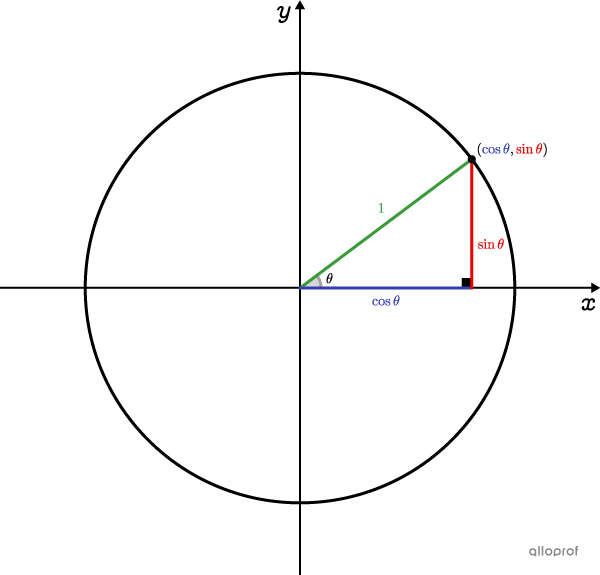
Note: |cos^2 \theta = (\cos\theta)^2.| The same is true for the other trigonometric ratios.
||\begin{align}\sin(A+B)&=\sin A\cos B+\cos A\sin B\\\\
\sin(A-B)&=\sin A\cos B-\cos A\sin B\\\\ \sin(2A)&=2 \sin A \cos A \end{align}||
||\begin{align}\cos(A+B)&=\cos A\cos B-\sin A\sin B\\\\
\cos(A-B)&=\cos A\cos B+\sin A\sin B\\\\ \cos(2A)&=\cos^2A-\sin^2 A\end{align}||
||\begin{align}\tan(A+B)&=\dfrac{\tan A+\tan B}{1-\tan A\tan B}\\\\\tan(A-B)&=\dfrac{\tan A -\tan B}{1+\tan A \tan B}\\\\ \tan(2A)&=\dfrac{2 \tan A}{1-\tan^2A}\end{align}||
The identities |\tan(A+B),| |\tan(A-B)| and |\tan(2A)| are valid only when the denominator is not equal to 0.
||1-\tan A\tan B\ne0||
||1+\tan A \tan B\ne0||
||1-\tan^2A\ne0||
The following identity will be proven: |\cos(A-B)=\cos A\cos B+\sin A\sin B.|
To do so, another identity must be used: |\cos(\alpha+\beta)=\cos \alpha\cos \beta-\sin \alpha\sin \beta.|
|\cos(A-B)| can also be written as |\cos \big(A+(-B)\big).| The above formula uses |\alpha=A| and |\beta =-B.| Applying the basic properties of the |\sin| and |\cos| ratios gives the following:||\begin{align}\cos\big(A+(-B)\big)&=\cos A\color{#3a9a38}{\cos (-B)}\sin A\color{#51b6c2}{\sin (-B)}\\&=\cos A\color{#3a9a38}{\cos B}-\sin A\color{#51b6c2}{(-\sin B)}\\&=\cos A\cos B+\sin A\sin B\\ \end{align}||The identity |\cos(A-B)=\cos A\cos B+\sin A\sin B| is therefore proven.
The following identity will be proven: |\sin (2A) = 2 \sin A \cos A.|
To do so, another identity must be used: |\sin(A+B) = \sin A \cos B + \cos A \sin B.|
|\sin (2A)| can also be written as |\sin (A + A).| The above formula uses |A=A| and |B=A.| Applying the commutative property of multiplication gives the following.||\begin{align}\sin(A+A) &= \sin A \cos A + \cos A \sin A\\&= \sin A \cos A + \sin A \cos A\\&= 2 \sin A \cos A\end{align}||The identity |\sin (2A) = 2 \sin A \cos A| is proven.
All these identities are helpful to determine the exact value of an expression when the angle is not one of the main angles.
-
Determine which combination of main angles results in |\theta.|
-
Choose the correct trigonometric identity.
-
Determine the value of the expression.
Determine the exact value of |\sin\left(\dfrac{7\pi}{12}\right).|
-
Determine which addition or subtraction of main angles results in |\boldsymbol{\theta}.|
Since |\dfrac{7\pi}{12}| is not a main angle, it must be broken down into a sum of or difference of main angles. The following addition is possible:||\begin{align}\dfrac{7\pi}{12}&=\dfrac{3\pi}{12}+\dfrac{4\pi}{12}\\\\&=\dfrac{\pi}{4}+\dfrac{\pi}{3}\end{align}|| -
Choose the correct trigonometric identity.
The addition |\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{3}\right)| is sought, so use the identity |\sin(A+B)=\sin A \cos B + \cos A \sin B,| where |A=\dfrac{\pi}{4}| and |B=\dfrac{\pi}{3}.| -
Determine the value of the expression.
||\begin{align}\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{3}\right)&=\sin \dfrac{\pi}{4} \times \cos\dfrac{\pi}{3}+ \cos\dfrac{\pi}{4} \times \sin\dfrac{\pi}{3}\\\\&=\dfrac{\sqrt{2}}{2} \times \dfrac{1}{2} + \dfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{3}}{2}\\\\&=\dfrac{\sqrt{2}}{4} + \dfrac{\sqrt{6}}{4}\\\\&=\dfrac{\sqrt{2}+\sqrt{6}}{4}\end{align}||
Answer: The exact value of |\sin\left(\dfrac{7\pi}{12}\right)| is |\dfrac{\sqrt{2}+\sqrt{6}}{4}.|
Determine the exact value of |\cos\left(\dfrac{\pi}{12}\right).|
-
Determine which addition or subtraction of main angles results in |\boldsymbol{\theta}.|
Since |\dfrac{\pi}{12}| is not a main angle, it must be broken down into a sum or a difference of main angles. The following subtraction is possible:||\begin{align}\dfrac{\pi}{12}&=\dfrac{4\pi}{12}-\dfrac{3\pi}{12}\\\\&= \dfrac{\pi}{3}-\dfrac{\pi}{4}\end{align}.|| -
Choose the correct trigonometric identity
The subtraction |\cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)| is sought, so use the identity |\cos(A-B)=\cos A \cos B+\sin A \sin B,| where |A=\dfrac{\pi}{3}| and |B=\dfrac{\pi}{4}.| -
Determine the value of the expression.
||\begin{align}\cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)&=\cos\dfrac{\pi}{3} \times \cos\dfrac{\pi}{4} + \sin \dfrac{\pi}{3} \times \sin\dfrac{\pi}{4}\\\\&=\dfrac{1}{2} \times \dfrac{\sqrt2}{2} + \dfrac{\sqrt{3}}{2} \times \dfrac{\sqrt2}{2} \\\\&=\dfrac{\sqrt2}{4}+\dfrac{\sqrt6}{4}\\\\&=\dfrac{\sqrt2+\sqrt6}{4}\end{align}||
Answer: The exact value of |\cos\left(\dfrac{\pi}{12}\right)| is |\dfrac{\sqrt2+\sqrt6}{4}.|
The answers of the last 2 examples are the same. The exact value of |\sin\left(\dfrac{7\pi}{12}\right)| is the same as |\cos\left(\dfrac{\pi}{12}\right).| This can be explained with the help of 2 basic properties of the |\sin| and |\cos| ratios: |\sin\left(\dfrac{\pi}{2}-\theta\right)=\cos\theta| and |\cos(-\theta)=\cos\theta.|||\begin{align}\sin\left(\dfrac{7\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\ \sin\left(\dfrac{6\pi}{12}+\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\sin\left(\dfrac{\pi}{2}-\left(-\dfrac{\pi}{12}\right)\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\cos\left(-\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\\\\\cos\left(\dfrac{\pi}{12}\right)&=\cos\left(\dfrac{\pi}{12}\right)\end{align}||
Determine the exact value of |\tan\left(\dfrac{23\pi}{12}\right).|
-
Determine which addition or subtraction of main angles results in |\boldsymbol{\theta}.|
Since |\dfrac{23\pi}{12}| is not a main angle, it must be broken down into a sum or difference of main angles. The following addition is possible:||\begin{align}\dfrac{23\pi}{12}&=\dfrac{21\pi}{12}+\dfrac{2\pi}{12}\\\\&=\dfrac{7\pi}{4}+\dfrac{\pi}{6}\end{align}.|| -
Choose the correct trigonometric identity.
The addition |\tan\left(\dfrac{7\pi}{4}+\dfrac{\pi}{6}\right)| is sought, so use the identity |\tan(A+B)=\dfrac{\tan A + \tan B}{1- \tan A \tan B},| where |A=\dfrac{7\pi}{4}| and |B=\dfrac{\pi}{6}.| -
Determine the value of the expression.
||\begin{align}\tan\left(\dfrac{7\pi}{4}+\dfrac{\pi}{6}\right)&= \dfrac{\tan\frac{7\pi}{4} + \tan\frac{\pi}{6}}{1 - \tan \frac{7\pi}{4} \times \tan \frac{\pi}{6}}\\\\&=\dfrac{-1 + \frac{\sqrt{3}}{3}}{1 - -1 \times \frac{\sqrt{3}}{3}}\\\\&=\dfrac{\frac{-3 + \sqrt{3}}{3}}{\frac{3+\sqrt{3}}{3}}\\\\&=\dfrac{-3 + \sqrt{3}}{3} \times \dfrac{3}{3+\sqrt{3}}\\\\&=\dfrac{-3+\sqrt{3}}{3+\sqrt{3}}\end{align}||Multiply by the conjugate of the denominator to rationalize the fraction.||\begin{align}\dfrac{-3+\sqrt{3}}{3+\sqrt{3}}&=\dfrac{\left(-3 + \sqrt{3}\right)}{\left(3+\sqrt{3}\right)} \color{#ec0000}{\times {\dfrac{\left(3 - \sqrt{3}\right)}{\left(3 - \sqrt{3}\right)}}}\\\\ &=\dfrac{-9+3\sqrt{3}+3\sqrt{3}-3}{9-3\sqrt{3}+3\sqrt{3}-3}\\\\&=\dfrac{-12 + 6\sqrt{3}}{6}\\\\&=-2+\sqrt{3}\end{align}||
Answer: The exact value of |\tan\left(\dfrac{23\pi}{12}\right)| is |-2+\sqrt{3}.|