The tangent ratio is one of the 3 main trigonometric ratios in a right triangle.
In a right triangle (sometimes called a right-angled triangle), the tangent of an angle |(\boldsymbol \theta)| corresponds to the ratio of the measure of the side opposite the angle to the adjacent side (or leg).
||\tan \theta=\dfrac{\text{The side $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{The side $\color{#333FB1}{\text{adjacent}}$ to angle }\theta}||
So, to find the tangent of the two acute angles in the following right triangle, we get the following 2 ratios.
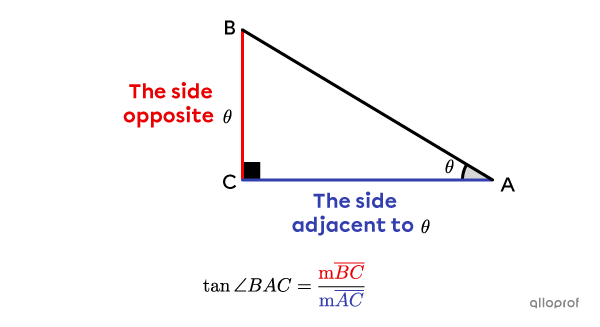
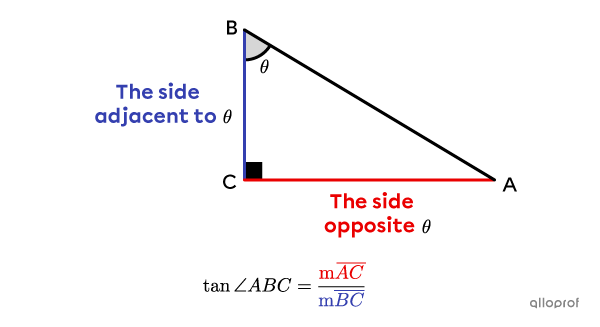
The tangent ratio is only used with acute angles. Never use the tangent ratio with a right angle.
The tangent ratio makes it possible to determine the measure of one of the 2 legs of a right triangle using the measure of an acute angle and the other leg.
Find the measure of the side |\overline{BC}| using the tangent ratio in the following triangle.

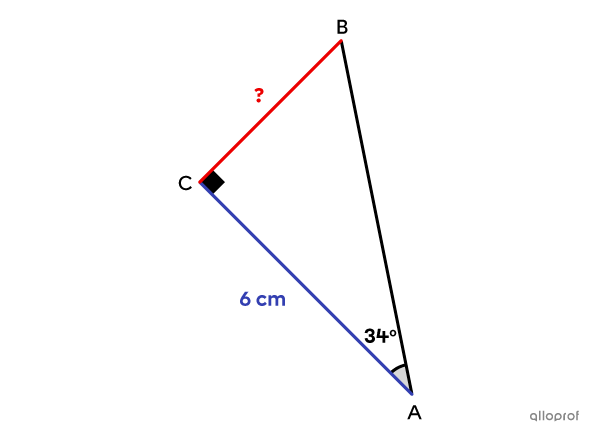
Since we know the measure of the side adjacent to the |34^{\circ}| angle, we can use the tangent ratio to find the measure of its opposite side |\overline{BC}.|
Substituting the measurements into the tangent ratio gives the following.
||\begin{align}\tan \theta&=\dfrac{\text{The side $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{The side $\color{#333FB1}{\text{adjacent}}$ to angle }\theta}\\\tan34^{\circ}&=\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#333FB1}{6}}\end{align}||
Using a calculator, find the measure of tan |34^{\circ}| and isolate the unknown side.
||\begin{align}0.6745&\approx\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#333FB1}{6}}\\4.0471&\approx\color{#ec0000}{\text{m}\overline{BC}}\end{align}||
Answer: Rounded to the nearest hundredth, the measure of side |\overline{BC}| is approximately |4.05\ \text{cm}.|
To ensure accuracy, it is best to calculate (on the calculator) in one step. If it is not possible, round to at least 3 or 4 decimal places during each step.
For example, when |\theta=65^{\circ}| and its adjacent side is |59\ \text{cm},| we obtain the following.
Calculating in 1 Step
|\begin{align}\tan65^{\circ}&=\dfrac{a}{{59}}\\\tan65^{\circ}\times59&=a\\\color{#EC0000}{126.53}&\approx a\end{align}|
Calculating in 2 Steps
|\begin{align}\tan65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{2.14}&\approx\dfrac{a}{59}\\2.14\times59&\approx a\\\color{#EC0000}{126.26}&\approx a\end{align}|
By calculating in 2 steps and keeping only 2 decimal places when calculating the tangent of the angle, the answer is 27 hundredths off from the correct response.
Determine the measure of the unknown side using the tangent ratio in the following right triangle.
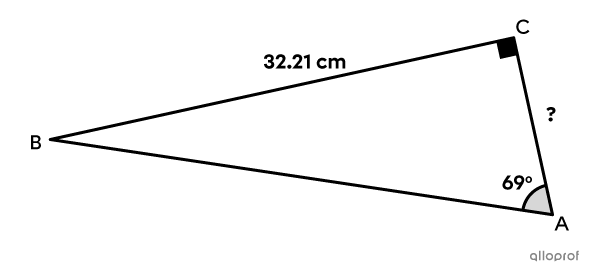

Since we know the measure of the side opposite the |69^{\circ}| angle, we can use the tangent ratio to find the measure of its adjacent side |\overline{AC}.|
||\begin{align}\tan \theta&=\dfrac{\text{The side $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{The side $\color{#333FB1}{\text{adjacent}}$ to angle }\theta}\\\tan69^{\circ}&=\dfrac{\color{#EC0000}{32.21}}{\color{#333FB1}{\text{m}\overline{AC}}}\\\end{align}||
Since the unknown measurement is in the denominator, we have the following. ||\begin{align}\dfrac{\tan69^{\circ}}{1}&=\dfrac{32.21}{\color{#333FB1}{\text{m}\overline{AC}}}\\\color{#333FB1}{\text{m}\overline{AC}}\times \tan69^{\circ}&=32.21\times 1\\\color{#333FB1}{\text{m}\overline{AC}}&=\dfrac{32.21}{\tan69^{\circ}}\\\color{#333FB1}{\text{m}\overline{AC}}&\approx \color{#333FB1}{12.36}\end{align}||
Answer: Rounded to the nearest hundredth, the measure of the side |\overline{AC}| is approximately |12.36\ \text{cm}.|
To find the measure of an acute angle in a right triangle using the tangent ratio, the measures of the legs opposite and adjacent the angle are required. This is the equivalent of asking: “Which angle creates a tangent ratio of…?”
We first find the tangent ratio and then press the |\tan^{-1}| (|arctan|) button on the calculator.
Using the tangent ratio, find the measure of angle |BAC| in the right triangle below.
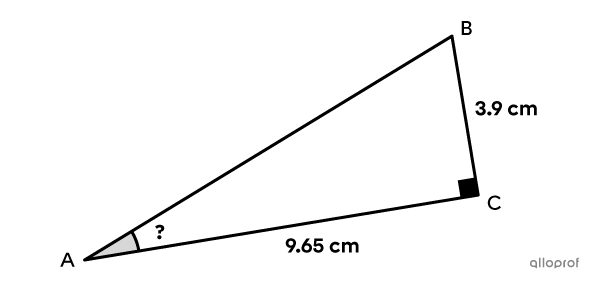
Since we know the measures of the legs opposite and adjacent to angle |BAC,| we can use the tangent ratio to find the measure of angle |BAC.|
||\begin{align}\tan \theta&=\dfrac{\text{The side $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{The side $\color{#333FB1}{\text{adjacent}}$ to angle }\theta}\\\tan \theta&=\dfrac{\color{#EC0000}{3.9}}{\color{#333FB1}{9.65}}\\\theta&=\color{#EC0000}{\tan^{-1}\left(\color{black}{\dfrac{3.9}{9.65}}\right)}\\\theta&\approx22^{\circ}\end{align}||
Answer: The measure of angle |BAC| is approximately |22^{\circ}.|
Here is part of a trigonometric table. It was used in mathematics before the invention of the calculator. The measure of certain angles and their tangent ratios are listed.
At the time, a mathematician would use the table to find the measure of an angle in a right triangle. For example, to find the measure of an angle where the tangent ratio is approximately |1.1918,| the angle would be |50^{\circ}.|
| Measurement of the Angle | Tangent Ratio |
|---|---|
| |10^{\circ}| | |\approx 0.1763| |
| |20^{\circ}| | |\approx 0.364| |
| |30^{\circ}| | |\approx 0.5774| |
| |40^{\circ}| | |\approx 0.8391| |
| |50^{\circ}| | |\approx 1.1918| |
| |60^{\circ}| | |\approx 1.7321| |
Fortunately, since the invention of the calculator, such tables are no longer necessary to find an angle in a right triangle.
The arc tangent function (denoted as |\tan^{-1}(x)|) is the inverse of the tangent function.
||\tan \theta=x\ \Leftrightarrow \ \tan^{-1}x=\theta||