Atoms are made up of subatomic particles: electrons and nucleons (protons and neutrons). Since the isotopes of a given element do not have the same number of neutrons in their nucleus, they also do not have the same nuclear stability. For example, the carbon-12 nucleus is stable, while the carbon-14 nucleus is unstable.
Nuclear stability is the stability of the nucleus of an atom. It is determined by the repulsion force of the protons and the nuclear force.
On the one hand, an atom with an unstable nucleus tends to decay, generating one or more stable nuclei. The transformation is accompanied by an emission of nuclear energy. The atom that undergoes this transformation is called radioactive.
On the other hand, an atom with a stable nucleus does not decay. To determine whether the nucleus of an atom is stable or not, we must determine the ratio of the number of neutrons and protons. The ratio is directly related to the forces within the nucleus.
The protons within the nucleus of the atom are positively charged. Therefore, they repel each other due to an electrical repulsive force.
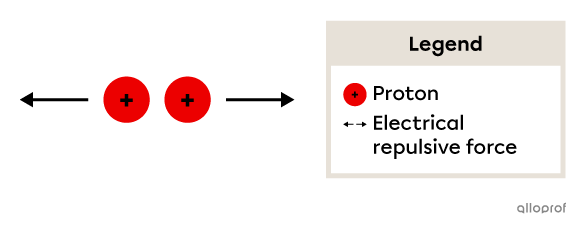
The more protons that are in the nucleus, the greater the repulsive force, which raises the question of how the protons can stay so close to each other in the nucleus.
The cohesion is because of the presence of neutrons within the nucleus. By being distributed among the protons, the neutrons minimize the repulsive force. Moreover, their presence generates a nuclear force, which promotes the attraction of nucleons.
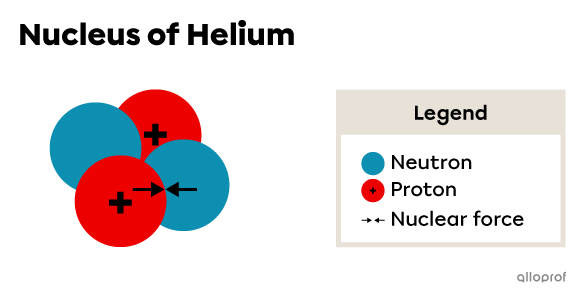
To ensure nuclear stability, the repulsive force between protons must be less than the nuclear force between nucleons. Accordingly, the ratio of the number of neutrons and protons must be optimal.
Here is what ensures nuclear stability of the elements in the periodic table.
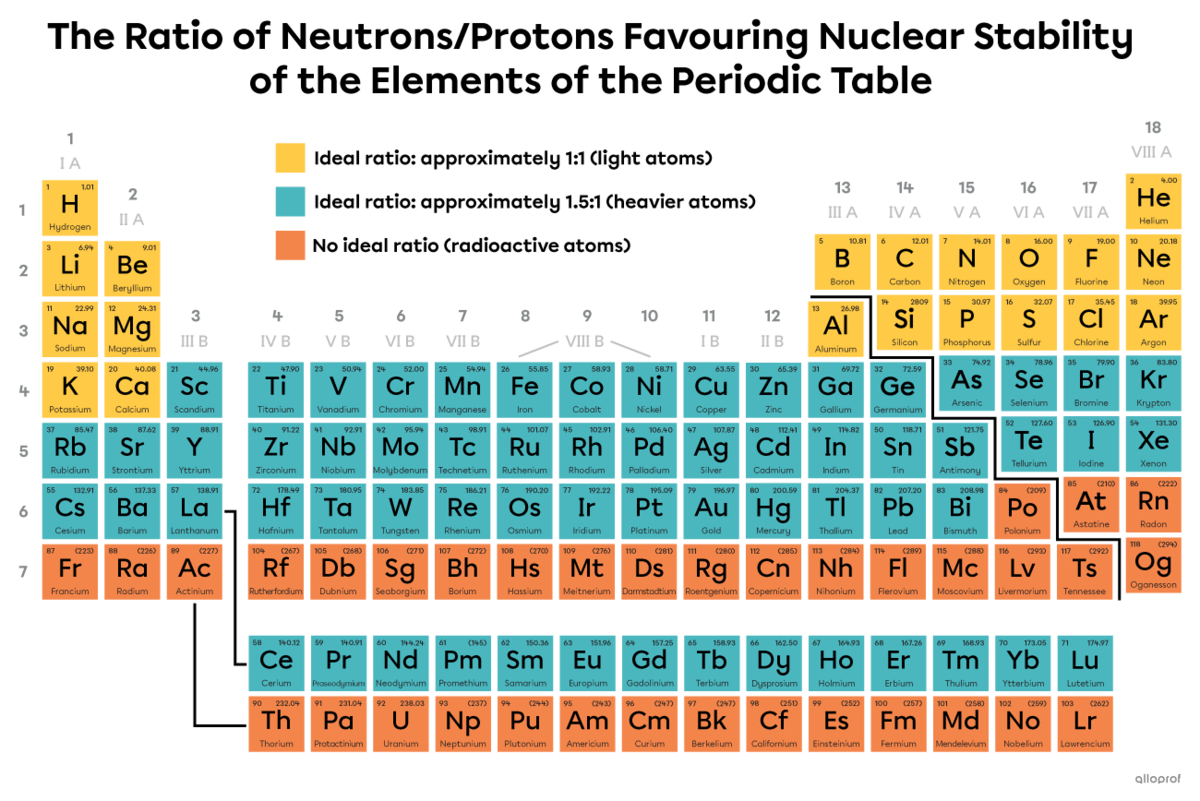
In the case of light atoms with an atomic number less than 21, a neutron/proton ratio close to 1:1 generally ensures the stability of an isotope. In other words, an equal number of neutrons and protons is generally beneficial for nuclear stability.
For heavier atoms with atomic numbers between 21 and 83, a ratio of 1.5:1 is often desirable.
Atoms with an atomic number above 83 are too heavy and are all radioactive. Their nucleus includes a lot of protons, so the repulsive force within the nucleus is very strong. Regardless of its number of neutrons, the nucleus is unstable and decays.
|
Isotope |
Neutron/proton ratio |
Ideal neutron/proton ratio |
Isotope stability |
|---|---|---|---|
|
|_1^2\text{H}| |
1:1 |
1:1 |
stable |
|
|_1^3\text{H}| |
2:1 |
1:1 |
unstable |
Hydrogen |(\text{H})| is a light atom with an atomic number of 1.
-
The isotope |_1^2\text{H}| consists of 1 neutron and 1 proton. The neutron/proton ratio is 1:1. The isotope is stable.
-
The isotope |_1^3\text{H}| consists of 2 neutrons and 1 proton. The neutron/proton ratio is 2:1, which means the isotope has too many neutrons to stabilize the nucleus. The isotope is unstable and radioactive.
|
Isotope |
Neutron/proton ratio |
Ideal neutron/proton ratio |
Isotope stability |
|---|---|---|---|
|
|_{56}^{138}\text{Ba}| |
1.46:1 |
1.5:1 |
stable |
|
|_{56}^{114}\text{Ba}| |
1.04:1 |
1.5:1 |
unstable |
Barium |(\text{Ba})| is an atom with atomic number 56. Its ideal neutron/proton ratio is approximately 1.5:1.
-
The isotope |_{56}^{138}\text{Ba}| includes 82 neutrons and 56 protons. The neutron/proton ratio is 1.46:1, which explains why the isotope is stable.
-
The isotope |_{56}^{114}\text{Ba}| includes 58 neutrons and 56 protons. The neutron/proton ratio is 1.04:1, far from the ideal ratio of 1.5:1. The isotope of barium does not have enough neutrons and is unstable.
Radium |(\text{Ra})| is a heavy atom with an atomic number of 88. Since radium’s atomic number is greater than 83, all of its isotopes have an unstable nucleus and are radioactive.
The mass of a stable nucleus should be equal to the sum of the mass of the nucleons forming its nucleus. However, it is not the case: the mass of the nucleus is smaller than its nucleons. It is referred to as the mass defect. The difference between the mass of the nucleons and the mass of the nucleus is transformed into energy. To determine the mass defect |(m_D),| we use the following formula.
|m_D = m_{nucleons} -m_{nucleus}|
where
|m_D| is the mass defect in atomic mass units |(\text{u})|
|m_{nucleons}| is the sum of the mass of the nucleons forming the atom in atomic mass units |(\text{u})|
|m_{nucleus}| is the mass of the nucleus in atomic mass units |(\text{u})|
A lithium isotope has 3 protons and 4 neutrons. What is the mass defect of the isotope, knowing that the mass of the nucleus is |7.01435\ \text{u}?|
Identify the data:
|\begin{align}
&\text{Number of protons:}\ Z=3\\
&\text{Number of neutrons:}\ N=4\\
&m_{nucleus}=7.01435\ \text{u}
\end{align}|
The mass of a proton and a neutron are reference data:
|\begin{align}
&m_{proton} = 1.00727 \ \text{u}\\
&m_{neutron}=1.00867\ \text{u}
\end{align}|
Begin by calculating the total mass of lithium nucleons. Identify the formula to use and then replace the data:
|\begin{align}
m_{nucleons}&=3m_{protons}+4m_{neutrons}\\
m_{nucleons}&=3 \times 1.00727\ \text{u}+4 \times 1.00867\ \text{u}\\
m_{nucleons}&=7.05649\ \text{u}
\end{align}|
To determine the mass defect, identify the formula to use and replace the data:
|\begin{align}
m_D&=m_{nucleons}-m_{nucleus}\\
m_D&=7.05649\ \text{u}-7.01435\ \text{u}\\
D_m&=0.04214\ \text{u}
\end{align}|
The mass defect of the isotope |_4^7\text{Li}| is |0.04214\ \text{u}.| This amount of matter was converted into energy during the formation of the lithium nucleus.
To calculate the amount of energy released by the mass difference, we must use Albert Einstein's equation, i.e., |E = mc^2.| So, the greater the mass defect, the greater the amount of energy released by the formation of the stable nucleus. Moreover, the larger the mass defect, the more stable the atom formed, because a greater amount of energy would be required to destabilize the nucleus.