Les atomes sont composés de particules subatomiques : les électrons et les nucléons (soit les protons et les neutrons). Puisque les isotopes d’un élément donné n’ont pas le même nombre de neutrons dans leur noyau, ils n’ont pas non plus la même stabilité nucléaire. Par exemple, le noyau du carbone 12 est stable, tandis que le noyau du carbone 14 est instable.
La stabilité nucléaire correspond à la stabilité du noyau d’un atome. Elle dépend de la force de répulsion des protons et de la force nucléaire.
Un atome dont le noyau est trop instable a tendance à se désintégrer de sorte qu’il génère un ou plusieurs noyaux plus stables. Cette transformation est accompagnée d’une émission d’énergie nucléaire. L’atome qui subit cette transformation est dit radioactif.
Par contre, un atome dont le noyau est stable ne se désintègre pas. Afin de déterminer si le noyau d’un atome est stable ou non, il faut tenir compte du ratio du nombre de neutrons et de protons qui constituent le noyau. Ce ratio est directement lié aux forces présentes au sein du noyau.
Les protons présents dans le noyau de l’atome sont chargés positivement. Cela implique qu’ils se repoussent mutuellement en raison d’une force de répulsion électrique.
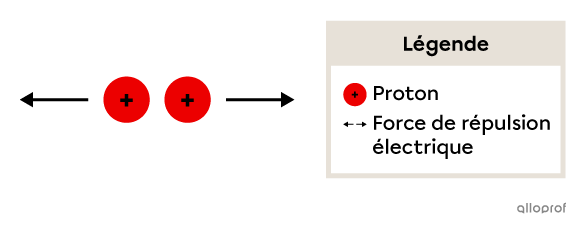
Plus il y a de protons dans le noyau, plus la force de répulsion est grande. On peut alors se demander comment les protons peuvent rester si proches les uns des autres dans le noyau.
C'est justement la présence des neutrons au sein du noyau qui contribue à sa cohésion. En se répartissant parmi les protons, les neutrons font en sorte que la force de répulsion soit minimisée. De plus, leur présence engendre une force nucléaire qui favorise l’attraction des nucléons.
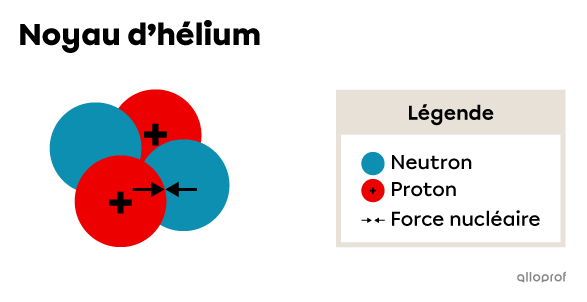
Afin de favoriser la stabilité nucléaire, la force de répulsion entre les protons doit être inférieure à la force nucléaire entre les nucléons. Pour cela, le ratio du nombre de neutrons et de protons doit être optimal.
Voici ce qui favorise la stabilité nucléaire des éléments du tableau périodique.

Dans le cas des atomes légers dont le numéro atomique est inférieur à 21, un ratio neutrons/protons proche de 1:1 favorise généralement la stabilité d’un isotope. Autrement dit, un nombre égal de neutrons et de protons est généralement favorable à la stabilité nucléaire.
Pour les atomes plus lourds dont le numéro atomique se situe entre 21 et 83, un ratio de 1,5:1 est souvent souhaitable.
Les atomes dont le numéro atomique se situe au-delà de 83 sont trop lourds et sont donc tous radioactifs. Leur noyau comprend beaucoup de protons, ce qui fait que la force de répulsion au sein du noyau est très grande. Quel que soit son nombre de neutrons, le noyau est instable et se désintègre.
| Isotope | Ratio neutrons/protons | Ratio idéal neutrons/protons | Stabilité de l'isotope |
|---|---|---|---|
| |_1^2\text{H}| | 1:1 | 1:1 | stable |
| |_1^3\text{H}| | 2:1 | 1:1 | instable |
L’hydrogène |(\text{H})| est un atome léger dont le numéro atomique est 1.
-
L’isotope |_1^2\text{H}| comprend 1 neutron et 1 proton. Le ratio neutrons/protons est donc de 1:1. Cet isotope est stable.
-
L’isotope |_1^3\text{H}| comprend 2 neutrons et 1 proton. Le ratio neutrons/protons est donc de 2:1, ce qui fait que cet isotope a trop de neutrons pour stabiliser son noyau. Cet isotope est instable et radioactif.
| Isotope | Ratio neutrons/protons | Ratio idéal neutrons/protons | Stabilité de l'isotope |
|---|---|---|---|
| |_{56}^{138}\text{Ba}| | 1,46:1 | 1,5:1 | stable |
| |_{56}^{114}\text{Ba}| | 1,04:1 | 1,5:1 | instable |
Le baryum |(\text{Ba})| est un atome dont le numéro atomique est 56. Son ratio neutrons/protons idéal est environ de 1,5:1.
-
L’isotope |_{56}^{138}\text{Ba}| comprend 82 neutrons et 56 protons. Le ratio neutrons/protons est donc de 1,46:1, ce qui explique pourquoi cet isotope est stable.
-
L’isotope |_{56}^{114}\text{Ba}| comprend 58 neutrons et 56 protons. Le ratio neutrons/protons est donc de 1,04:1, loin du ratio idéal de 1,5:1. Cet isotope du baryum n’a pas assez de neutrons et est donc instable.
Le radium |(\text{Ra})| est un atome lourd dont le numéro atomique est 88. Puisque son numéro atomique est supérieur à 83, tous ses isotopes ont un noyau instable et sont radioactifs.
La masse d’un noyau stable devrait être égale à la somme des masses des nucléons qui forment son noyau. Toutefois, ce n’est pas le cas : la masse du noyau est plus petite que celle de ses nucléons. C’est ce qu’on appelle le défaut de masse. La différence entre la masse des nucléons et la masse du noyau est transformée en énergie. Pour déterminer le défaut de masse |(D_m)|, il faut utiliser la formule suivante.
|D_m = m_{nucléons} -m_{noyau}|
où
|D_m| représente le défaut de masse en unités de masse atomique |(\text{u})|
|m_{nucléons}| représente la somme de la masse des nucléons formant l’atome en unités de masse atomique |(\text{u})|
|m_{noyau}| représente la masse du noyau en unités de masse atomique |(\text{u})|
Un isotope de lithium comprend 3 protons et 4 neutrons. Quel est le défaut de masse de cet isotope, sachant que la masse de son noyau est |7{,}014\ 35\ \text{u}|?
On identifie les données :
|\begin{align}
&\text{nombre de protons :}\ Z=3\\
&\text{nombre de neutrons :}\ N=4\\
&m_{noyau}=7{,}014\ 35\ \text{u}
\end{align}|
Les masses d’un proton et d’un neutron sont des données de référence :
|\begin{align}
&m_{proton} = 1{,}007\ 27 \ \text{u}\\
&m_{neutron}=1{,}008\ 67\ \text{u}
\end{align}|
On commence par calculer la masse totale des nucléons du lithium. On identifie la formule à employer et on remplace les données :
|\begin{align}
m_{nucléons}&=3m_{protons}+4m_{neutrons}\\
m_{nucléons}&=3 \times 1{,}007\,27\ \text{u}+4 \times 1{,}008\,67\ \text{u}\\
m_{nucléons}&=7{,}056\,49\ \text{u}
\end{align}|
Afin de déterminer le défaut de masse, on identifie la formule à employer et on remplace les données :
|\begin{align}
D_m&=m_{nucléons}-m_{noyau}\\
D_m&=7{,}056\,49\ \text{u}-7{,}014\,35\ \text{u}\\
D_m&=0{,}042\,14\ \text{u}
\end{align}|
Le défaut de masse de l’isotope |_4^7\text{Li}| est donc de |0{,}042\,14\ \text{u}.| Cette quantité de matière a été convertie en énergie lors de la formation de ce noyau de lithium.
Pour calculer la quantité d’énergie libérée par cette différence de masse, il faut utiliser l’équation d’Albert Einstein, soit |E = mc^2.| Ainsi, plus le défaut de masse sera grand, plus la quantité d’énergie libérée par la formation du noyau stable sera grande. De plus, plus le défaut de masse est grand, plus l’atome formé est stable, car une plus grande quantité d’énergie serait nécessaire pour déstabiliser son noyau.