Contrairement aux autres solides, l'aire d'une sphère ne peut pas être divisée en différentes parties comme l'aire latérale ou l'aire de la base. En fait, l'aire latérale et l'aire totale représentent la même surface puisqu'il n'y a pas de base. En ce qui concerne la boule, son aire totale correspond à l'espace délimité par la sphère.
Bien qu'elle soit entièrement composée d'une seule surface courbe, il est possible de calculer la superficie de la sphère.
||A_T = 4 \pi r^2|| où ||\begin{align}A_T &: \text{Aire totale}\\r &: \text{rayon}\end{align}||
Étant donné sa surface courbe, il peut y avoir une certaine ressemblance entre cette formule et celle qui permet de calculer l'aire d'un disque. Dans les 2 cas, une seule mesure est nécessaire pour l'utilisation de cette formule, soit la mesure du rayon.
Pour que toutes les balles de baseball utilisées dans la Ligue majeure soient identiques, on les recouvre du même matériau.
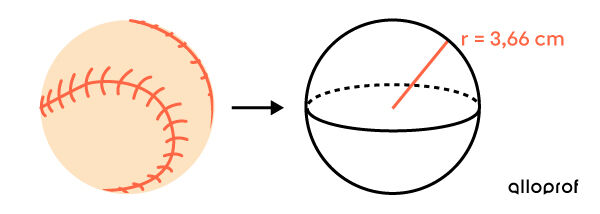
Selon les informations données, quelle quantité de matériau, en |\text{cm}^2,| doit-on utiliser pour recouvrir une balle?
-
Identifier le solide
Puisque c'est l'aire qu'on recherche, on fait référence à la sphère. -
Appliquer la formule ||\begin{align} A_T &= 4 \pi r^2 \\ &= 4 \pi (3{,}66)^2\\ &\approx 168{,}33 \ \text{cm}^2 \end{align}||
-
Interpréter la réponse
L'aire totale de la sphère est donc d'environ |168{,}33 \ \text{cm}^2.|
Même si une seule mesure est nécessaire pour compléter les calculs, il faut savoir que le rayon de la sphère est la mesure du segment qui relie le centre de cette dernière à sa limite extérieure. Ainsi, le rayon n'est pas obligé d'être parfaitement horizontal ou vertical. De plus, d'autres dimensions peuvent être associées à la mesure du rayon.
Les dimensions dans une sphère
Le rayon de la sphère peut être associé à sa largeur ou à sa hauteur.
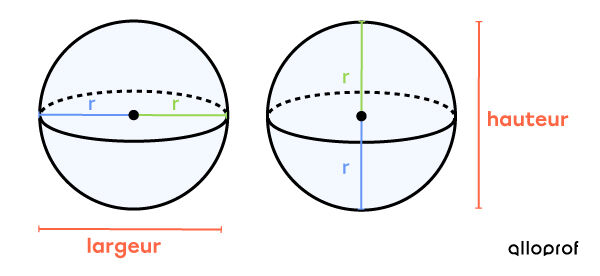
Dans les deux cas, |\text{Largeur} = 2 r = \text{Hauteur}.| Cela correspond aussi au diamètre de la sphère.
En divisant la sphère en deux parties égales, on obtient un autre genre de solide avec des propriétés un peu différentes.
Il arrive qu’on doive calculer l’aire d’une demi-sphère et qu’aucune nouvelle surface n’apparaisse lorsqu’on coupe la sphère en 2. C'est une sphère ouverte. Dans ce cas, il s’agit de calculer l’aire de la sphère complète et de diviser le résultat en 2. Le contexte permettra d’établir s’il s’agit d’une demi-sphère ouverte ou fermée.
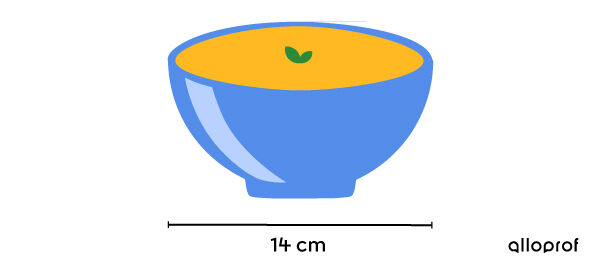
Lors de la fabrication d’un bol d’argile, on applique un enduit dans le bol pour s’assurer de ne pas abimer l’argile en mangeant. Quelle surface d’enduit a-t-on besoin pour le bol ci-dessous, si on suppose que le bol est parfaitement demi-sphérique?
-
Identifier le solide
Puisque c'est l'aire de l’intérieur du bol qu'on recherche, on fait référence à l’aire d’une demi-sphère ouverte dont le diamètre est de |14\ \text{cm}.| Le rayon du bol est donc de |7\ \text{cm}.| -
Appliquer la formule
L’aire totale de la sphère se calcule ainsi : ||\begin{align} A_T &= 4 \pi r^2\\ &= 4 \pi (7)^2\\&=196\pi\\ &\approx 615{,}75 \ \text{cm}^2\end{align}|| Donc, l’aire de la demi-sphère est |\dfrac{615{,}75}{2} \approx 307{,}88\ \text{cm}^2 .| -
Interpréter la réponse
La surface d’enduit est donc d’environ |307{,}88 \ \text{cm}^2.|
Une demi-sphère fermée est une sphère dont la moitié a été conservée et dont l'ouverture a été couverte par un disque. Il est possible de déterminer l'aire de cette portion en additionnant l'aire de la demi-sphère et l'aire du disque formé par cette coupe.
En d'autres mots, pour obtenir l’aire totale d’une demi-sphère fermée, il faut ajouter l’aire du disque à la moitié de la surface de la sphère.
||A_T = 2 \pi r^2 + \pi r^2||
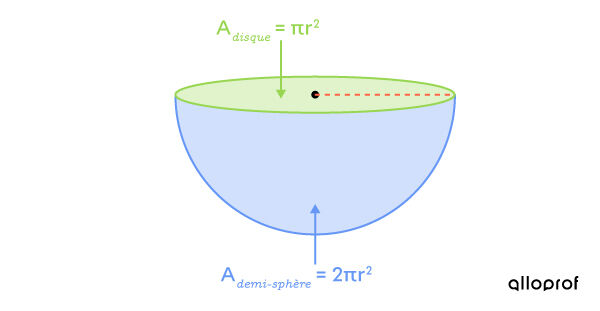
L’application concrète de cette formule demande une attention particulière quant à l'ordre des opérations à effectuer.
Afin d'assurer une distribution uniforme de la chaleur dans une bouilloire de forme demi-sphérique, on veut la recouvrir de nichrome (alliage de nickel et de chrome).
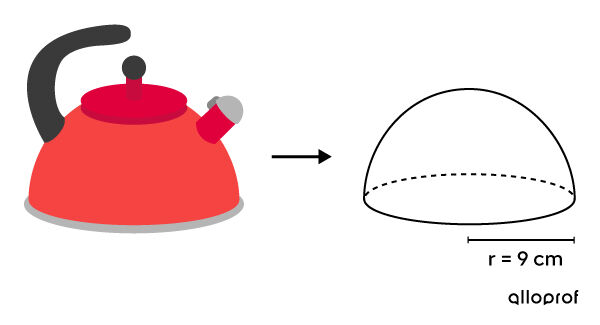
Quel sera le cout d'une telle opération s'il en coute |0{,}09\ $| pour couvrir une surface de |1\ \text{cm}^2| avec du nichrome?
-
Identifier le solide
Comme il s’agit d’une bouilloire, la demi-sphère est fermée pour contenir l’eau. -
Appliquer la formule ||\begin{align} A_T &= 2 \pi r^2 + \pi r^2 \\ &= 2 \pi (9)^2 + \pi (9)^2 \\ &=162\pi + 81\pi \\ &=243\pi \\ &\approx 763{,}41 \ \text{cm}^2 \end{align}||
-
Interpréter la réponse
Maintenant qu'on connait l'aire en |\text{cm}^2,| il suffit de la multiplier par le cout par |\text{cm}^2 :| ||763{,}41\ \text{cm}^2 \times 0{,}09\ $/\text{cm}^2 \approx 68{,}71\ $||
Finalement, le cout pour recouvrir la bouilloire sera de |68{,}71\ $.|
Dans d'autres circonstances, on pourrait s'intéresser à la mesure du rayon ou encore du diamètre d’une sphère alors que l’aire totale est donnée, c’est ce qui s’appelle trouver une mesure manquante d'une sphère à partir de l'aire. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule de l’aire totale associée aux sphères.