Dans certains problèmes, il arrive que l'on connaisse l'aire d'un solide ainsi que toutes ses mesures, sauf une. Il faut donc savoir trouver cette mesure manquante.
La procédure à suivre pour trouver une mesure manquante dans un solide est généralement la même peu importe son type. Voici les principales étapes.
-
Identifier les mesures données.
-
Déterminer la formule à utiliser.
-
Remplacer les variables par les mesures données.
-
Isoler la variable recherchée.
Afin de permettre à la clientèle de voir le produit emballé, une compagnie de jouets insiste pour remplacer certaines faces de ses boites cubiques en carton par un épais matériau transparent. Pour commander le tout, la compagnie a besoin de connaitre les dimensions d’une boite. En sachant que l'aire totale d’une boite est de |2\ 646\ \text{cm}^2,| détermine la mesure des arêtes de ce cube.

-
Identifier les mesures données
Aire totale de la boite : |A_T=2\ 646 \ \text{cm}^2| -
Déterminer la formule à utiliser
Puisqu'il est question de l'aire totale, on utilise : ||A_T = 6 c^2|| -
Remplacer les variables par les mesures données ||2 \ 646 = 6 \color{#7CCA51}{c}^2||
-
Isoler la variable recherchée ||\begin{align} 2 \ 646 &= 6 \color{#7CCA51}{c}^2 \\ \color{#EC0000}{\frac{\color{black}{2 \ 646}}{6}} &= \color{#EC0000}{\frac{\color{black}{6}\color{#7CCA51}{c}^\color{black}{2}}{6}} \\ 441 &= \color{#7CCA51}{c}^2\\ \color{#EC0000}{\sqrt{\color{black}{441}}} &= \color{#EC0000}{\sqrt{\color{#7CCA51}{c}^\color{black}{2}}}\\ 21\ \text{cm} &= \color{#7CCA51}{c}\end{align}||
Réponse : La mesure d'une arête de ce cube est de |21\ \text{cm}.|
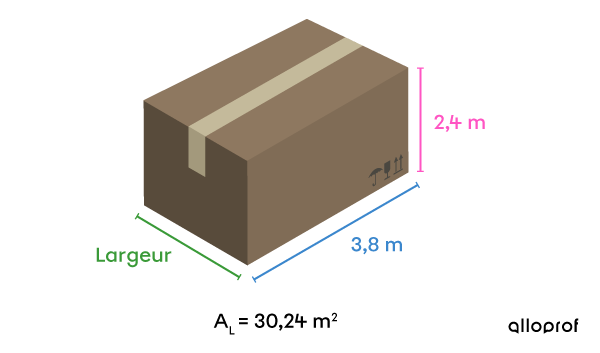
Avant de faire sa livraison, un camionneur doit s'assurer que les dimensions de l'objet à transporter n'excèdent pas la largeur de sa remorque. Pour son prochain transport, il a seulement accès aux mesures identifiées sur l'image. Pour l'aider, détermine la mesure de la largeur de cette boite.
-
Identifier les mesures données
Aire latérale de la boite : |A_L=30{,}24\ \text{m}^2|
Longueur de la base : |\color{#3B87CD}{L}=3{,}8\ \text{m}|
Hauteur de la boite : |\color{#FF55C3}{h}=2{,}4\ \text{m}| -
Déterminer la formule à utiliser
Puisqu'il est question de l'aire latérale d'un prisme à base rectangulaire, on utilise : ||A_L = P_b \times h|| -
Remplacer les variables par les mesures données ||30{,}24 = (\color{#3A9A38}{l} +\color{#3A9A38}{l} + \color{#3B87CD}{3{,}8} + \color{#3B87CD}{3{,}8}) \times \color{#FF55C3}{2{,}4}||
-
Isoler la variable recherchée ||\begin{align} 30{,}24 &=(\color{#3A9A38}{l} +\color{#3A9A38}{l} + \color{#3B87CD}{3{,}8} + \color{#3B87CD}{3{,}8}) \times \color{#FF55C3}{2{,}4}\\ 30{,}24 &= (2\color{#3A9A38}{l} + 7{,}6)\times 2{,}4 \\ 30{,}24 &= 4{,}8 \color{#3A9A38}{l} + 18{,}24\\ 30{,}24 \color{#EC0000}{- 18{,}24} &= 4{,}8 \color{#3A9A38}{l} +18{,}24 \color{#EC0000}{ - 18{,}24}\\ 12 &= 4{,}8 \color{#3A9A38}{l}\\ \color{#EC0000}{\dfrac{\color{black}{12}}{4{,}8}} &= \color{#EC0000}{\dfrac{\color{black}{4{,}8}\color{#3A9A38}{l}}{4{,}8}}\\ 2{,}5\ \text{m} &= \color{#3A9A38}{l}\end{align}||
Réponse : La largeur du prisme à base rectangulaire est de |2{,}5\ \text{m}.|
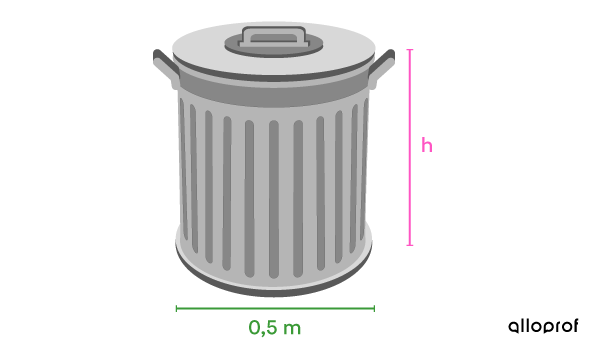
Sergueï veut enduire sa nouvelle poubelle cylindrique et refermable d’un enduit antirouille. Sa voisine lui parle d’un produit qui permet de couvrir sa poubelle de |1{,}335\ \text{m}^2| avec une seule canne d’enduit. Toutefois, la poubelle de Sergueï est deux fois plus haute que celle de sa voisine. Si sa voisine possède une poubelle de |0{,}5\ \text{m}| de diamètre, quelle est la hauteur de la poubelle de Sergueï?
-
Identifier les mesures données
Aire totale de la poubelle de la voisine : |A_T=1{,}335\ \text{m}^2|
Diamètre de la poubelle de la voisine : |\color{#3A9A38}{d=0{,}5\ \text{m}}| -
Déterminer la formule à utiliser
Puisqu'il est question de l'aire totale d'un cylindre, on utilise : ||A_T = 2A_b+A_L|| -
Remplacer les variables par les mesures données
Dans le cas présent, il faut diviser le diamètre de la poubelle en 2 pour obtenir le rayon nécessaire dans la formule. ||\begin{align}\color{#7CCA51}{\text{rayon}}&=\color{#3A9A38}{\text{diamètre}}\div2\\&=\color{#3A9A38}{0{,}5}\div2\\&=\color{#7CCA51}{0{,}25\ \text{m}}\end{align}|| ||\begin{align}A_T &= 2\times \pi \color{#7CCA51}r^2+2 \pi \color{#7CCA51}r \color{#FF55C3}{h}\\ 1{,}335 &=2\times \pi(\color{#7CCA51}{0{,}25})^2+ 2\pi (\color{#7CCA51}{0{,}25}) \times \color{#FF55C3}{h}\end{align}|| -
Isoler la variable recherchée ||\begin{align}1{,}335 &=2\times \pi(\color{#7CCA51}{0{,}25})^2+ 2\pi (\color{#7CCA51}{0{,}25}) \times \color{#FF55C3}{h}\\1{,}335&\approx 0{,}39 + 1{,}57\color{#FF55C3}{h}\\1{,}335\color{#EC0000}{-0{,}39}&\approx 0{,}39 + 1{,}57\color{#FF55C3}{h}\color{#EC0000}{-0{,}39}\\ 0{,}945&\approx1{,}57\color{#FF55C3}{h}\\ \color{#EC0000}{\dfrac{\color{black}{0{,}945}}{1{,}57}}&\approx \color{#EC0000}{\dfrac{\color{black}{1{,}57}\color{#FF55C3}{h}}{1{,}57}}\\0{,}60\ \text{m}&\approx\color{#FF55C3}{h}\end{align}||
Réponse : Comme la poubelle de Sergueï est deux fois plus haute que celle de sa voisine, la hauteur de la poubelle de Sergueï est d’environ |2\times 0{,}6=1{,}2\ \text{m}.|
Quelle est la mesure du rayon d'une balle de tennis si on sait qu'un contenant de forme cylindrique pouvant contenir exactement 3 balles a une aire latérale de |379{,}84\ \text{cm}^2?|
-
Identifier les mesures données
Aire latérale du contenant : |A_L=379{,}84\ \text{cm}^2| -
Déterminer la formule à utiliser
Puisqu'il est question de l'aire latérale d'un cylindre, on utilise : ||A_L = 2 \pi rh|| -
Remplacer les variables par les mesures données
Dans le cas présent, on peut trouver la mesure de la hauteur à l'aide de celle du rayon des balles.
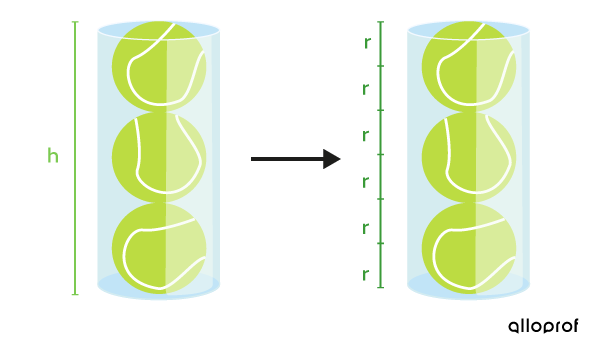
||\begin{align} A_L &= 2 \pi r \times \color{#7CCA51}{h}\\ 379{,}84 &= 2 \pi r \times \color{#7CCA51}{6}\color{#3A9A38}{r}\end{align}||
-
Isoler la variable recherchée ||\begin{align} 379{,}84 &= 2 \pi \color{#3A9A38}{r} \times 6\color{#3A9A38}{r}\\ \color{#ec0000}{\dfrac{\color{black}{379{,}84}}{12\pi}} &= \color{#ec0000}{\dfrac{\color{black}{12 \pi\color{#3A9A38}{r}^2}}{12\pi}} \\ \color{#ec0000}{\sqrt{\color{black}{10{,}08}}} &\approx \color{#ec0000}{\sqrt{\color{#3A9A38}{r}^{\color{black}{2}}}}\\ 3{,}17\ \text{cm} &\approx \color{#3A9A38}{r}\end{align}||
Réponse : Les balles de tennis ont un rayon d’environ |3{,}17\ \text{cm}.|
Gabriela désire acheter un encensoir décoratif pour son salon. L’encensoir est une pyramide octogonale régulière. Le problème, c’est que Gabriela ne sait pas si la décoration peut tenir sur une tablette de |15\ \text{cm}| de profondeur.
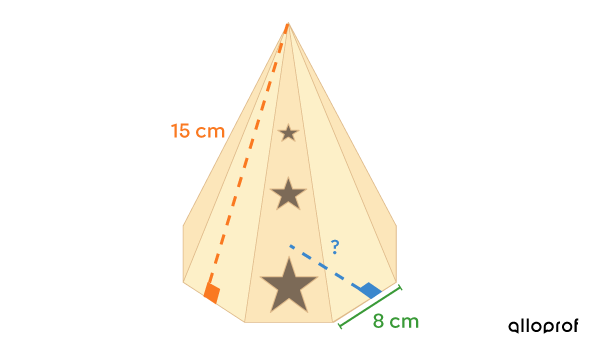
Gabriela connait l’aire totale de l’encensoir, qui est de |789{,}12\ \text{cm}^2.| L’apothème de la pyramide est de |15\ \text{cm}| et la mesure d’un côté de l’octogone est de |8\ \text{cm}.|
L’encensoir peut-il entrer sur la tablette si l’apothème de la base |(\color{#3B87CD}{a_b})| est perpendiculaire au mur?
-
Identifier les mesures données
Aire totale de la pyramide : |A_T=789{,}12 \ \text{cm}^2|
Apothème de la pyramide : |\color{#FA7921}{a_p=15\ \text{cm}}|
Mesure des côtés de l’octogone : |\color{#3A9A38}{c=8\ \text{cm}}|
Nombre de côtés d’un octogone : |n=8\ \text{côtés}| -
Déterminer la formule à utiliser
Dans le cas d’une pyramide régulière à base octogonale, la formule pour calculer l’aire totale est : ||\begin{align}A_T &= A_L+A_B\\&=\dfrac{P_b\times \color{#FA7921}{a_p}}{2}+\dfrac{\color{#3A9A38}{c}\times \color{#3B87CD}{a_b}\times n}{2}\end{align}|| -
Remplacer les variables par les mesures données ||\begin{align}789{,}12&=\dfrac{(8\times \color{#3A9A38}{8})\times\color{#FA7921}{15}}{2}+\dfrac{\color{#3A9A38}{8}\times \color{#3B87CD}{a_b}\times 8}{2}\end{align}||
-
Isoler la variable recherchée ||\begin{align}789{,}12&=480+32\color{#3B87CD}{a_b}\\789{,}12\color{#EC0000}{-480}&=480+32\color{#3B87CD}{a_b}\color{#EC0000}{-480}\\309{,}12&=32\color{#3B87CD}{a_b}\\\ \color{#EC0000}{\dfrac{\color{black}{309{,}12}}{32}}&=\color{#EC0000}{\dfrac{\color{black}{32}\color{#3B87CD}{a_b}}{32}}\\9{,}66\ \text{cm}&=\color{#3B87CD}{a_b}\end{align}||
Réponse : Puisque l’apothème de la base est de |9{,}66\ \text{cm},| la largeur de la pyramide, si elle est perpendiculairement appuyée au mur, est de |2\times 9{,}66=19{,}32\ \text{cm}.| Ainsi, comme la tablette mesure |15\ \text{cm},| l’encensoir ne peut pas y tenir.
Dans le cas d’une pyramide régulière dont la base est un polygone régulier, il faut faire attention de ne pas confondre l’apothème de la base avec celui de la pyramide.
Comme l’apothème est généralement identifié par la variable |a,| il est suggéré de les différencier en y ajoutant un indice. Ainsi, l’apothème de la pyramide devient |a_p| et l’apothème de la base devient |a_b.| Le choix de l’indice ou de la façon d’identifier ces 2 mesures peut différer.
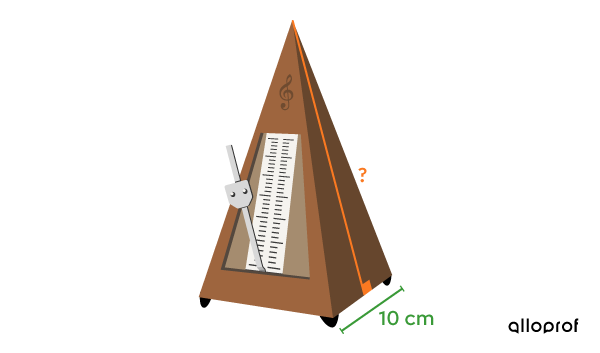
Stefan est un adepte de piano et il utilise fréquemment un vieux métronome qui a la forme d’une pyramide à base carrée.
Pour vernir son métronome, il désire connaitre la mesure de l’apothème de la pyramide. Il sait que la base du métronome mesure |10\ \text{cm}| et que son aire totale est de |512{,}4\ \text{cm}^2.|
Quelle est la mesure de l’apothème du métronome?
-
Identifier les mesures données
Aire totale de la pyramide : |A_T=512{,}4 \ \text{cm}^2|
Mesure des côtés du carré : |\color{#3A9A38}{c=10\ \text{cm}}| -
Déterminer la formule à utiliser
Dans le cas d’une pyramide régulière à base carrée, la formule pour calculer l’aire totale est : ||\begin{align}A_T &= A_L+A_B\\&=\dfrac{P_b\times \color{#FA7921}{a_p}}{2}+\color{#3A9A38}{c}^2\end{align}|| -
Remplacer les variables par les mesures données ||\begin{align}512{,}4&=\dfrac{(4\times \color{#3A9A38}{10})\times\color{#FA7921}{a_p}}{2}+\color{#3A9A38}{10}^2\end{align}||
-
Isoler la variable recherchée ||\begin{align}512{,}4&=20\color{#FA7921}{a_p}+100\\512{,}4\color{#EC0000}{-100}&=20\color{#FA7921}{a_p}+100\color{#EC0000}{-100}\\412{,}4&=20\color{#FA7921}{a_p}\\\ \color{#EC0000}{\dfrac{\color{black}{412{,}4}}{20}}&=\color{#EC0000}{\dfrac{\color{black}{20\color{#FA7921}{a_p}}}{20}}\\20{,}62\ \text{cm}&=\color{#FA7921}{a_p}\end{align}||
Réponse : L’apothème du métronome est de |20{,}62\ \text{cm}.|
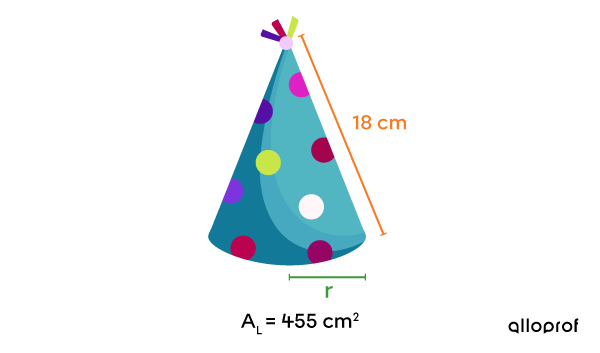
À l'occasion de la fête de leur enfant, des parents se procurent des chapeaux en forme de cône afin d'en distribuer à tous les invités. Pour s'assurer que le modèle trouvé en ligne soit assez grand pour la tête des enfants, ils veulent connaitre la mesure du rayon du cercle à la base de cet accessoire.
-
Identifier les mesures données
Aire latérale du cône : |A_L=455\ \text{cm}^2|
Mesure de l’apothème du cône : |\color{#FA7921}{a=18\ \text{cm}}| -
Déterminer la formule à utiliser
Dans le cas du cône, la formule pour calculer l’aire latérale est : ||A_L = \pi \times \color{#3A9A38}{r} \times \color{#FA7921}{a}|| -
Remplacer les variables par les mesures données ||455 = \pi \times\color{#3A9A38}{r} \times \color{#FA7921}{18}||
-
Isoler la variable recherchée ||\begin{align} \color{#EC0000}{\dfrac{\color{black}{455}} {18}} &= \color{#EC0000}{\dfrac{\color{black}{\pi \color{#3A9A38}{r} \times \color{#FA7921}{18}}}{18}}\\ 25{,}28 &\approx \pi \color{#3A9A38}{r}\\ \color{#EC0000}{\dfrac{\color{black}{25{,}28}}{\pi}} &\approx \color{#EC0000}{\dfrac{\color{black}{\pi}\color{#3A9A38}{r}}{\pi}} \\ 8{,}05\ \text{cm} &\approx \color{#3A9A38}{r}\end{align}||
Réponse : Ce modèle de chapeau de fête a un rayon d’environ |8{,}05\ \text{cm}.|
Comme la pyramide et le cône ont une allure similaire, la démarche à suivre pour trouver la mesure de l'apothème d’un cône est la même que celle pour trouver cette même mesure dans une pyramide.
Afin d'attirer plus de touristes, un centre de villégiature veut installer une remontée mécanique sur une montagne pour offrir une vue panoramique. Pour mener ce projet à terme, le centre a besoin de connaitre la distance entre le pied de la montagne et son sommet.
Grâce aux cartes topographiques de la région, on peut estimer l'aire latérale de cette montagne conique à |1{,}7\ \text{km}^2| et la mesure du rayon de sa base à |500\ \text{m}.| Selon ces données, quelle doit être la longueur, au mètre près, de la remontée mécanique?
-
Identifier les mesures données
Aire latérale du cône (comme il faut travailler dans les mêmes unités que la mesure du rayon, une conversion d’unités s’impose) : |A_L=1{,}7\ \text{km}^2=1\ 700\ 000\ \text{m}^2|
Mesure du rayon du cône : |\color{#3B87CD}{r=500\ \text{m}}| -
Déterminer la formule à utiliser
Puisqu'on travaille avec l'aire latérale du cône et qu'on cherche l'apothème, on utilise : ||A_L = \pi \times \color{#3B87CD}{r} \times \color{#FA7921}{a}|| -
Remplacer les variables par les mesures données ||1\ 700\ 000 = \pi \times \color{#3B87CD}{500}\times\color{#FA7921}{a}||
-
Isoler la variable recherchée ||\begin{align}\color{#EC0000}{\dfrac{\color{black}{1\ 700\ 000}}{500}} &= \color{#EC0000}{\dfrac{\color{black}{\pi \times \color{#3B87CD}{500}\times}\color{#FA7921}{a}}{500}}\\ 3\ 400 &= \pi \color{#FA7921}{a}\\ \color{#EC0000}{\dfrac{\color{black}{3\ 400}}{\pi}} &= \color{#EC0000}{\dfrac{\color{black}{\pi}\color{#FA7921}{a}}{\pi} }\\ 1\ 082{,}25\ \text{m} &\approx \color{#FA7921}{a}\end{align}||
Réponse : La remontée mécanique serait d'une longueur approximative de |1\ 082\ \text{m}.|
Pour la pyramide comme pour le cône, il arrive parfois qu’on doive déterminer la hauteur du solide à partir de l’aire alors que cette mesure ne se retrouve pas dans la formule de l’aire. Dans ces cas, il faut d’abord trouver l’apothème du solide ou le rayon de la base. Ensuite, il faut faire une étape supplémentaire, soit calculer la hauteur à l’aide du théorème de Pythagore.
Que ce soit pour une pyramide ou pour un cône, la démarche à suivre est très similaire.
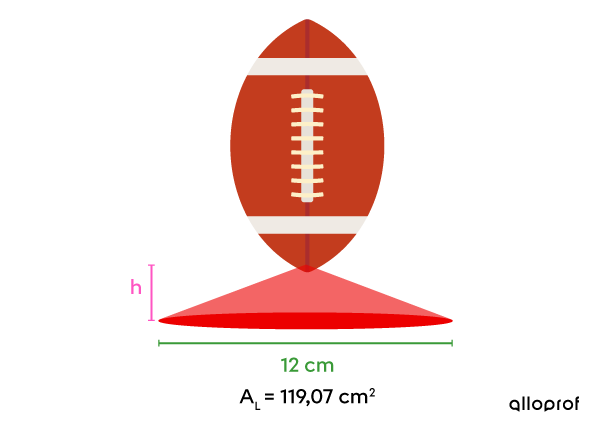
Lors du botté d'envoi d'une partie de football américain, il arrive souvent que les botteurs utilisent un petit support en forme de cône pour tenir le ballon en position verticale.
Si la pointe du ballon coïncide avec l'apex du cône, à quelle distance du sol se trouve le ballon lorsqu'il est sur son support?
-
Identifier les mesures données
Aire latérale du cône : |A_L=119{,}07\ \text{cm}^2|
Mesure du rayon du cône : |\color{#3A9A38}{r}=\dfrac{12}{2}=\color{#3A9A38}{6\ \text{cm}}| -
Déterminer la formule à utiliser
Puisqu'on connait l'aire latérale du cône, on ne peut pas trouver directement sa hauteur. Il faut d’abord déterminer l’apothème du cône avec la formule suivante. ||A_L = \pi \times \color{#3A9A38}{r} \times \color{#FA7921}{a}|| -
Remplacer les variables par les mesures données ||119{,}07 = \pi \times \color{#3A9A38}{6} \times \color{#FA7921}{a}||
-
Isoler la variable recherchée ||\begin{align} \color{#EC0000}{\dfrac{\color{black}{119{,}07}}{6}} &=\color{#EC0000}{\dfrac{\color{black}{\pi \times \color{#3A9A38}{6} \times \color{#FA7921}{a}}}{6}}\\19{,}845 &= \pi \color{#FA7921}{a}\\\color{#EC0000}{\dfrac{\color{black}{19{,}845}}{\pi}} &=\color{#EC0000}{\dfrac{\color{black}{\pi} \color{#FA7921}{a}}{\pi}}\\ 6{,}32\ \text{cm} &\approx \color{#FA7921}{a}\end{align}||
Pour trouver la hauteur du cône, on forme un triangle rectangle délimité par la hauteur, l'apothème et la moitié de la base, comme représenté sur l’image suivante. Par la suite, on utilise le théorème de Pythagore.
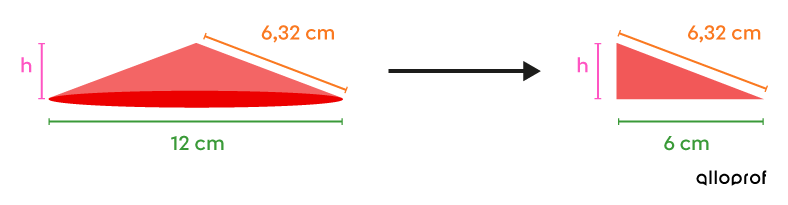
||\begin{align} \color{#FF55C3}{a}^2 + \color{#3A9A38}{b}^2 &= \color{#FA7921}{c}^2\\\\ \color{#FF55C3}{h}^2 + \color{#3A9A38}{6}^2 &= \color{#FA7921}{6{,}32}^2\\ \color{#FF55C3}{h}^2 + 36 &\approx 39{,}94\\ \color{#FF55C3}{h}^2 + 36 \color{#ec0000}{-36} &\approx 39{,}94 \color{#EC0000}{-36} \\ \color{#FF55C3}{h}^2 &\approx 3{,}94 \\ \color{#EC0000}{\sqrt{\color{#FF55C3}{h}^\color{black}{2}}} &\approx \color{#EC0000}{\sqrt{\color{black}{3{,}94}}}\\ \color{#FF55C3}{h} &\approx 1{,}98\ \text{cm}\end{align}||Réponse : Le ballon se retrouve à une distance d'environ |1{,}98\ \text{cm}| du sol.
Comme on peut le voir dans l’exemple précédent, il faut inévitablement trouver la mesure de l’apothème avant de déduire celle de la hauteur à l'aide du théorème de Pythagore. Autrement dit, trouver la hauteur d’un cône ou d’une pyramide à partir de l’aire exige quelques calculs de plus que ceux pour trouver l’apothème.
Si, au lieu de l’aire latérale, on connait le volume d’un cône ou d’une pyramide ainsi que les dimensions de sa base, on peut alors trouver la hauteur directement. En effet, on retrouve bel et bien cette mesure dans la formule du volume des cônes et des pyramides. La formule du volume de ces solides est |V= \dfrac{A_b \times h}{3}.|
S’il faut trouver l’apothème d’un de ces solides à partir du volume, il faut donc commencer par trouver la hauteur. Puis, en utilisant le théorème de Pythagore, on trouve l’apothème. Pour voir un exemple, consulte la fiche Trouver la mesure de l’apothème d’une pyramide ou d’un cône.
Quelle est la hauteur, en millimètres, d'une boule de billard traditionnelle?

-
Identifier les mesures données
Aire totale de la boule de billard : |A_T=10\ 273{,}58 \ \text{mm}^2| -
Déterminer la formule à utiliser
Puisqu'il est question de l'aire d'une sphère, on utilise la formule suivante. ||A = 4 \pi r^2|| -
Remplacer les variables par les mesures données ||10 \ 273{,}58 = 4 \pi r^2||
-
Isoler la variable recherchée ||\begin{align} \color{#EC0000}{\dfrac{\color{black}{10 \ 273{,}58}}{4\pi}} &= \color{#EC0000}{\dfrac{\color{black}{4 \pi r^2}}{4\pi}}\\ 817{,}55 &\approx r^2\\ \color{#EC0000}{\sqrt{\color{black}{817{,}55}}} &\approx \color{#EC0000}{\sqrt{\color{black}{r^2}}} \\28{,}59\ \text{mm} &\approx r \end{align}||
Puisque la hauteur d'une sphère est équivalente à 2 fois son rayon, on peut déduire que |\color{#3A9A38}{h}= 28{,}59 \times 2 = 57{,}18 \ \text{mm}.|

Réponse : La hauteur de la boule de billard est de |57{,}18 \ \text{mm}.|
Pour valider ta compréhension à propos des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante :
