Le volume d'une boule correspond à l'espace à l'intérieur de la sphère qui la délimite. On utilise le mot sphère quand il est question de superficie (aire) et le mot boule quand il est question d'espace occupé (volume). Ainsi, le volume d’une boule est plus approprié que le volume d’une sphère.
Pour trouver son volume, il suffit d'appliquer cette formule :
||V = \dfrac{4 \pi r^3}{3}||
où
||\begin{align}V&: \text{Volume}\\ r&: \text{rayon de la boule}\end{align}||
Comme c’est le cas pour trouver l’aire d’une sphère, seule la mesure du rayon est nécessaire pour calculer le volume d’une boule.
En ce qui concerne le volume d'une demi-boule, il suffit de calculer le volume de la boule entière pour ensuite diviser le résultat par 2.
Pour entretenir l'eau d'une piscine, une compagnie fabrique du chlore en granules en forme de boule.
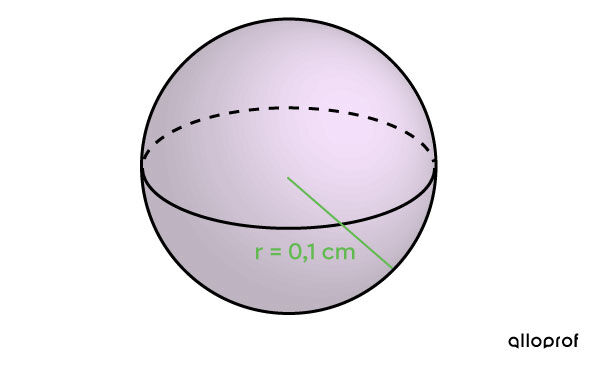
En supposant que les granules soient bien compactés pour que la perte d'espace soit négligeable, combien y en aura-t-il dans un récipient de |5\ 000\ \text{cm}^3?|
-
Identifier le solide
Dans le contexte, il est clairement mentionné qu'il s'agit d'une boule. -
Appliquer la formule ||\begin{align} V &= \dfrac{4 \pi r^3}{3}\\\\&= \dfrac{4 \pi (0{,}1)^3}{3}\\\\&\approx 0{,}004\ \text{cm}^3\end{align}||
-
Interpréter la réponse
Pour déterminer le nombre de granules, il ne reste qu'à faire la division suivante : ||5\ 000\ \text{cm}^3 \div 0{,}004\ \text{cm}^3 /\text{granule} = 1\ 250\ 000 \ \text{granules}||
Il y aura |1\ 250\ 000\ \text{granules}| dans le récipient de |5\ 000\ \text{cm}^3.|
Finalement, il ne faut pas oublier que la relation entre le rayon, la hauteur et la largeur d'une boule est la même que celle que l’on établit dans le cas d’une sphère.
Dans certains problèmes, on peut rechercher la mesure du rayon alors que le volume est donné. C’est ce qui s’appelle trouver une mesure manquante d'une boule à partir du volume.