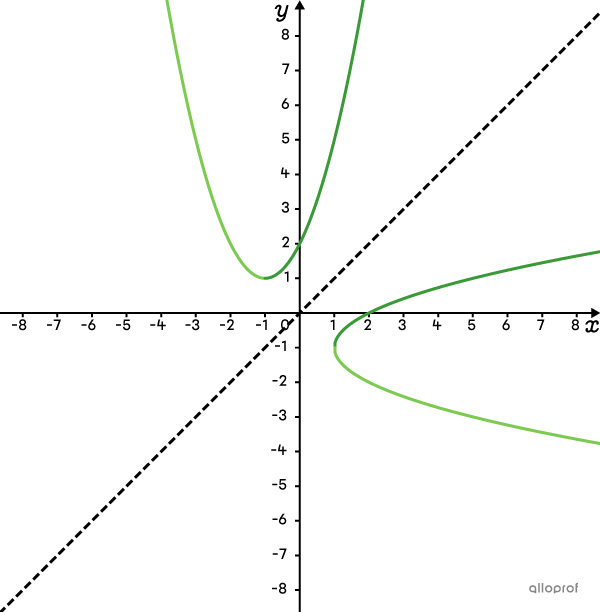
La fonction racine carrée est une branche de la réciproque de la fonction polynomiale de degré 2. Autrement dit, tracer une fonction racine carrée revient à tracer une demi-parabole horizontale.
Le tableau ci-dessous indique l’allure de la courbe selon le rôle des paramètres |\color{#3B87CD}{a}| et |\color{#EC0000}{b}| de la fonction racine carrée.
| |\color{#EC0000}{b}<0| | |\color{#EC0000}{b}>0| | |
|---|---|---|
| |\color{#3B87CD}{a}>0| |
La fonction est définie en haut et à gauche du sommet. 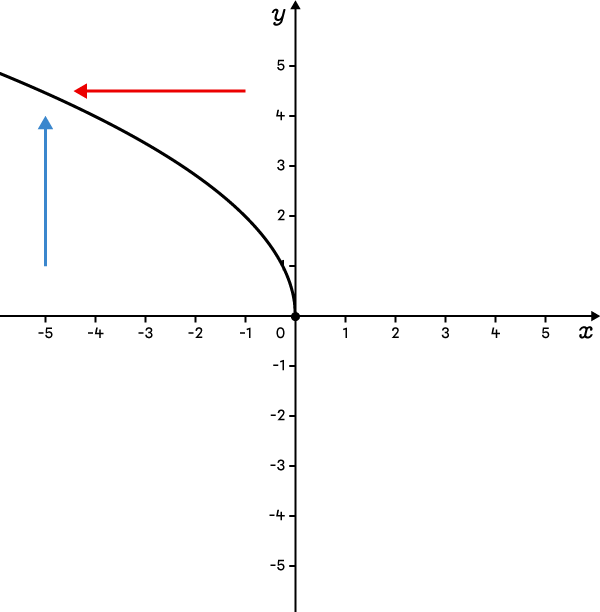 |
La fonction est définie en haut et à droite du sommet. 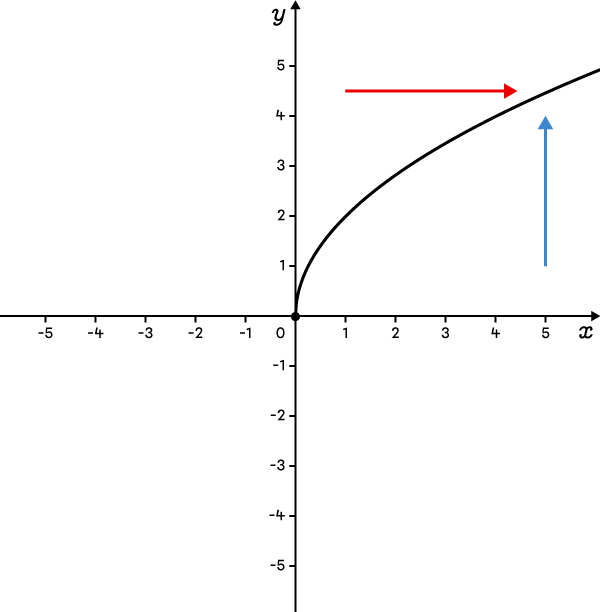 |
| |\color{#3B87CD}{a}<0| |
La fonction est définie en bas et à gauche du sommet. 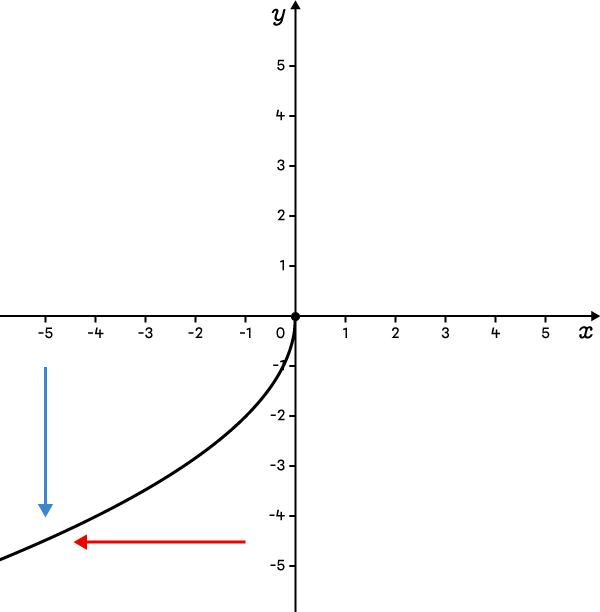 |
La fonction est définie en bas et à droite du sommet. 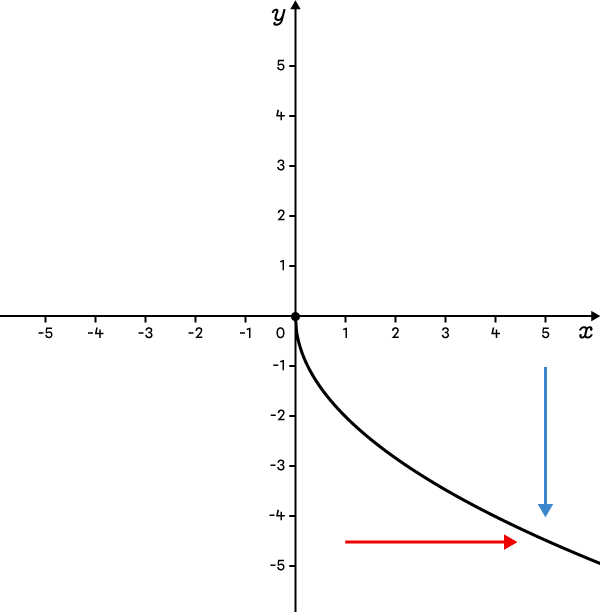 |
Voici la marche à suivre lorsqu’on veut tracer, dans un plan cartésien, une fonction racine carrée de la forme |f(x)=a\sqrt{bx}.|
-
Placer le sommet aux coordonnées |(\color{#51B6C2}{0},\color{#FA7921}{0})| et déterminer l’allure de la courbe en analysant les paramètres |\color{#3B87CD}{a}| et |\color{#EC0000}{b}.|
-
Calculer et placer des points supplémentaires.
-
Tracer la fonction racine carrée.
On veut tracer la fonction |f(x)=2\sqrt{-3x}.|
-
Placer le sommet et déterminer l’allure de la courbe
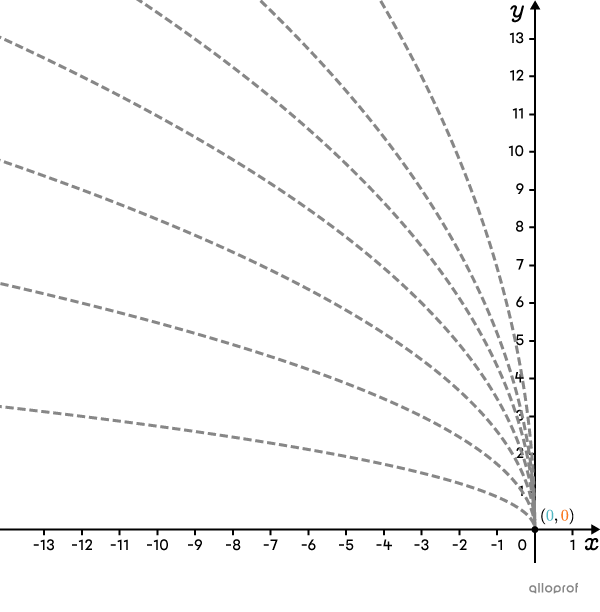
D’abord, on place un point à l’origine du plan cartésien. Ensuite, on analyse les paramètres |\color{#3B87CD}{a}| et |\color{#EC0000}{b}.|
Le paramètre |\color{#3B87CD}{a}| vaut |\color{#3B87CD}{2},| ce qui implique que la courbe est en haut de l’origine.
Le paramètre |\color{#EC0000}{b}| vaut |\color{#EC0000}{-3},| alors on en déduit que la courbe est à gauche de l’origine.
-
Calculer et placer des points supplémentaires
On doit choisir des valeurs de |\color{#3a9a38}{x}| et calculer leur |\color{#3a9a38}{f(x)}| associée. Comme on sait que le courbe est à gauche du sommet, on choisit des valeurs de |\color{#3a9a38}{x}| négatives. On prend d’abord |\color{#3a9a38}{x}=\color{#3a9a38}{-2}.|||\begin{align}f(\color{#3a9a38}{x})&=2\sqrt{-3\color{#3a9a38}{x}}\\ f(\color{#3a9a38}{-2})&=2\sqrt{-3(\color{#3a9a38}{-2})}\\ f(\color{#3a9a38}{-2})&=2\sqrt{6}\\ \color{#3a9a38}{f(-2)}&\approx\color{#3a9a38}{4{,}9}\\ \end{align}||Plus il y a de points dont on connait les coordonnées, plus le tracé de la courbe est précis. Ainsi, avec |\color{#3a9a38}{x}=\color{#3a9a38}{-3}| et |\color{#3a9a38}{x}=\color{#3a9a38}{-12},| on obtient les points |(-3,6)| et |(-12,12).|
On place maintenant les 3 points dans le plan cartésien.
On remarque que ces 3 points sont situés à gauche et en haut de l’origine, ce qui confirme ce qui a été déterminé à l'étape 2.

-
Tracer la fonction
En reliant tous les points, on obtient la courbe de la fonction |f(x)=2\sqrt{-3x}.|

Lorsqu’on choisit des valeurs de |x| pour placer des points supplémentaires dans le plan cartésien, il est préférable de s’assurer que le résultat sous la racine est un nombre carré. Ceci permet d’éviter d’avoir des coordonnées approximatives.
Dans l’exemple précédent, |x=-2| n’est pas le meilleur choix, car |-3\times-2=6.| Effectivement, |6| n’est pas un nombre carré, car |\sqrt{6}\approx2{,}45.| Par contre, |x=-3| et |x=-12| donnent respectivement |9| et |36| sous la racine, deux nombres carrés.
Voici la marche à suivre lorsqu’on veut tracer dans un plan cartésien une fonction racine carrée de la forme |f(x)=a\sqrt{b(x-h)}+k.|
-
Placer le sommet aux coordonnées |(\color{#51B6C2}{h},\color{#FA7921}{k})| et déterminer l’allure de la courbe en analysant les paramètres |\color{#3B87CD}{a}| et |\color{#EC0000}{b}.|
-
Calculer et placer des points supplémentaires.
-
Tracer la fonction racine carrée.
À l’étape 3, bien que ce ne soit pas toujours possible, il est préférable de calculer la valeur du zéro (l’abscisse à l’origine) et de l’ordonnée à l’origine.
On veut tracer la fonction |f(x)=-3\sqrt{x-2}+6.|
-
Placer le sommet aux coordonnées |(h,k)| et déterminer l’allure de la courbe en analysant les paramètres |a| et |b|
Dans cette fonction, |\color{#51b6c2}{h}=\color{#51b6c2}{2}| et |\color{#fa7921}{k}=\color{#fa7921}{6}.| On place donc le sommet à |(\color{#51b6c2}{2},\color{#fa7921}{6}).|
Le paramètre |\color{#3B87CD}{a}| vaut |\color{#3B87CD}{-3},| ce qui implique que la courbe est en bas du sommet.
Le paramètre |\color{#EC0000}{b}| vaut |\color{#EC0000}{1},| alors on en déduit que la courbe est à droite du sommet.

-
Calculer et placer des points supplémentaires
De l’image précédente, on déduit que toutes les courbes potentielles croisent l’axe des |x.| Ceci implique que la fonction possède assurément un abscisse à l’origine. Par contre, il n’y a pas d’ordonnée à l’origine, car aucune des courbes ne croise l’axe des |y.| On remplace |f(x)| par |0| afin de calculer l’abscisse à l’origine.||\begin{align}\color{#3a9a38}{f(x)}&=-3\sqrt{x-2}+6\\ \color{#3a9a38}{0}&=-3\sqrt{x-2}+6\\ -6&=-3\sqrt{x-2}\\ 2&=\sqrt{x-2}\\ 4&=x-2\\ 6&=x\\ \end{align}||Ainsi, la courbe a un zéro à |(6,0).| Quant à l’ordonnée à l’origine, la fonction |f(x)=-3\sqrt{x-2}+6| n’en possède pas. En effet, en remplaçant |x| par |0,| on obtient |\sqrt{-2},| ce qui est impossible.
On calcule les coordonnées de quelques points supplémentaires afin d’avoir un tracé plus précis. Comme on sait que le courbe est à droite du sommet, on choisit des valeurs de |x| supérieures à |2.| On prend d’abord |x=11.|||\begin{align}f(\color{#3a9a38}{x})&=-3\sqrt{\color{#3a9a38}{x}-2}+6\\ f(\color{#3a9a38}{11})&=-3\sqrt{\color{#3a9a38}{11}-2}+6\\ f(11)&=-3\sqrt{9}+6\\ f(11)&=-3\times3+6\\ \color{#3a9a38}{f(11)}&=\color{#3a9a38}{-3}\\ \end{align}||De la même manière, avec |x=18,| on obtient un autre point dont les coordonnées sont |(18,-6).|
On place l’abscisse à l’origine et les 2 points dans le plan cartésien.
On remarque que ces 3 points sont situés à droite et en bas du sommet, ce qui confirme ce qui a été déterminé à l'étape 2.

-
Tracer la fonction
En reliant tous les points, on obtient le graphique de la fonction |f(x)=-3\sqrt{x-2}+6.|
